Пусть допустимое множество альтернатив состоит из 4 альтернатив Х= а1 5, с, d . На этом множестве задано следующее отношение предпочтения >= ( а, f), (Ь, f), (d, с), (5, а), (а, с), (5, с) . Можете ли вы построить функцию полезности представляющую данные предпочтения Если нет, то почему Если да, то постройте. [c.39]
Если / = , =... = = 0, то а = ( х . .. х ) — опорное решение исходной задачи (9.19) — (9.21). Если же среди чисел yl, yl,. . ., Ут есть положительные, то исходная задача (9.19) — (9.21) имеет пустое допустимое множество. [c.201]
Обе из рассматриваемых задач имеют пустые допустимые множества. [c.204]
Обратим внимание читателя на то, что разумна несколько иная постановка задачи о выборе оптимального рациона. Ограничения (5.6) накладывают слишком жесткие ограничения на допустимый рацион, поскольку требуют точного выполнения зоотехнических норм по каждому из питательных веществ. В действительности же ничего страшного не происходит, если для некоторых питательных веществ их количество превзойдет норму. Поэтому переформулируем ограничения (5.6) несколько по-иному. Пусть 1г — множество индексов питательных веществ, для которых зоотехническая норма должна выполняться в точности, а /2 — множество индексов тех питательных веществ, сверхнормативное потребление которых не может принести вред. Тогда вместо (5.6) можно выписать такие ограничения [c.177]
Совместность системы ограничений — обязательное условие разрешимости модели в случае несовместности этой системы допустимое множество является пустым. [c.237]
Теорема 4.1. Пусть А — множество допустимых решающих правил (апостериорных пли априорных) многоэтапной стохастической задачи с безусловными статистическими ограничениями [c.198]
Если ЗМП имеет хотя бы одно допустимое решение (т.е. ее допустимое множество не пусто), она называется допустимой, если ЗМП не имеет ни одного допустимого решения (т.е. ее допустимое множество пусто), она называется недопустимой. [c.130]
Прежде всего, для того, чтобы лучше понять, в чем же выражается неприятный эффект нелинейности, проведем сравнение задач линейного и нелинейного программирования. Начнем с множества допустимых планов. В задачах линейного программирования оно выпуклое, с конечным числом крайних точек (напоминаем, что крайней точкой называется всякая точка множества, которая не является внутренней ни для какого отрезка, целиком принадлежащего этому множеству). Это сразу становится понятным, если вспомнить, что границами множества служат гиперплоскости. В задачах же нелинейного программирования (в том случае, когда нелинейны ограничения) множество допустимых планов может быть невыпуклым, может иметь бесконечное число крайних точек. Например, пусть допустимая область на плоскости ХОУ определяется такими ограничениями [c.72]
Например, пусть допустимая область на плоскости XOY определяется ограничениями (X — I)2 + (Y— 1)2 <[ 1 YX <[ 1.. На рис. 8 видно, что эта область невыпуклая (отрезок, соединяющий любые две точки на гиперболе, не принадлежит этой области). Кроме того, все точки, лежащие на ограничивающей область дуге окружности, являются крайними, т. е. имеется бесчисленное множество крайних точек. [c.98]
Пусть допустимое потребительское множество Х= х Л+ х ,х2- целые , потребитель имеет фиксированный доход R > 0, цены на товары задаются вектором реМ++. Изобразите графически бюджетное множество потребителя. [c.54]
Пусть допустимое потребительское множество Х=М+, потребитель имеет начальный запас со=(1,1), цены на товары задаются вектором реМ++. Изобразите графически бюджетное множество потребителя, в случае если в экономике ввели налог с продаж, взимаемый как процент от цены. Является ли бюджетное множество выпуклым [c.54]
Пусть допустимое потребительское множество Х=М+, R > 0 и реМ++. Рассмотрим потре- [c.55]
Мы должны показать, что для двух произвольных векторов р1 и р2 при (К а < 1 выполняется е(ар + (1-а)р2, ж) ае(р ж) + (1-а)е(р2, ж). Пусть Я- решение двойственной задачи при ценах ра=ар + (1-а)р2, т.е. ЯеЛ,(ра, ж). Отметим, раЯ = е(ра, ж). Допустимое множество Л,еХ т/ > х не зависит от р, поэтому потребительский набор Я допустим в двойственной задаче как при ценах р1, так и при ценах р2. Из определения функции расходов и допустимости Я имеем е(р ж)< р Я и е(р2, ж) < р2Я. Отсюда [c.70]
Мы считаем, что М = N, где N — множество натуральных чисел. Пусть — семейство всех конечных подмножеств множества N, элементы которого мы будем обозначать N, TV, TV",.... Для любой группы N G обозначим через XN множество альтернатив, доступных группе N, из которого группа должна осуществить свой выбор. Пусть DN — семейство всех возможных задач, с которыми могут столкнуться члены N. Каждый элемент DN задается допустимым множеством, то есть некоторым подмножеством XN, удовлетворяющим каким-либо условиям, а также данными, описывающими окружающую обстановку, включающими, как правило, предпочтения участников на допустимом множестве. [c.214]
Если допустимое множество задачи линейного программирования не пусто, а целевая функция ограничена снизу (для задачи минимизации) на этом множестве, то задача линейного программирования имеет оптимальное решение. [c.187]
В двойственной задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена снизу. При этом у прямой задачи допустимое множество оказывается пустым. [c.204]
Найдя множество допустимых решений задачи (1.5), определим допустимые пределы нарушения ограничений (1.2) и (1.4). Это можно определить в диалоге ЛПР (технолога-оператора процесса). Пусть di=1,0 d2=0,5 d3=1,0. [c.48]
Для выбора наиболее рационального решения с помощью математических методов прежде всего необходимо указать систему величин, характеризующих качество каждого из возможных решений (систему так называемых показателей). Пусть совокупность возможных решений описывается как множество допустимых значений переменных математической модели (3.25), т. е. в виде z
Проблема принятия решений в условиях неопределенности по своей сложности значительно превосходит эту задачу в детерминированном случае, т. е. в отсутствие неопределенности. Пусть, например, имеется единственный показатель функционирования изучаемой экономической системы и этот показатель зависит от неопределенного параметра. Рассмотрим следующую проблему как выбрать такое управление х, принадлежащее заданному множеству допустимых управлений X, чтобы показатель W(x, у), где у — неопределенный параметр, принимал возможно большее значение Если бы величина параметра у была известна заранее (например, у = г/ ), то мы получили бы обычную оптимизационную задачу [c.152]
Пусть А и Л 2 два различных метода, применяемых для прогнозирования одного и того же множества номенклатур k. Тогда при уровне q допустимой ошибки А следует считать лучше метода А2, если p >pz (р и р2 — характеристики соответственно методов А и As). При такой постановке задачи получается следующая блок-схема решения задачи на ЭВМ. Для прогнозирования потребности номенклатур из данного множества k используется несколько методов А, AZ.....AN. По каждому методу подсчитывается число pt(t=], N), вероятность получения точности прогноза q, где q — задано и постоянно для всех методов. Этот этап задачи можно назвать этапом выбора метода прогнозирования. Следующий этап заключается в нахождении значений yjn+i,. .., Ujn+m по методу, для которого число р максимально. [c.122]
Пусть инвестор осуществляет выбор из множества допустимых портфелей Р на основе [c.49]
Теорема 1. Пусть для любой иерархи из множества допустимых ие- [c.31]
Пусть целевая функция АЭ /( ) и множество его допустимых [c.72]
Функция Лагранжа. Пусть х — элемент множества допустимых решений D такой, что значение /о( ) не меньше значения /о для любого другого элемента L>, т.е. х — оптимальное решение задачи НП. Выясним, каким условиям кроме неравенства [c.330]
| Рис. 9.17. Функция достижимости и ее выпуклая оболочка для случая, когда множество допустимых решений исходной задачи НП пусто | 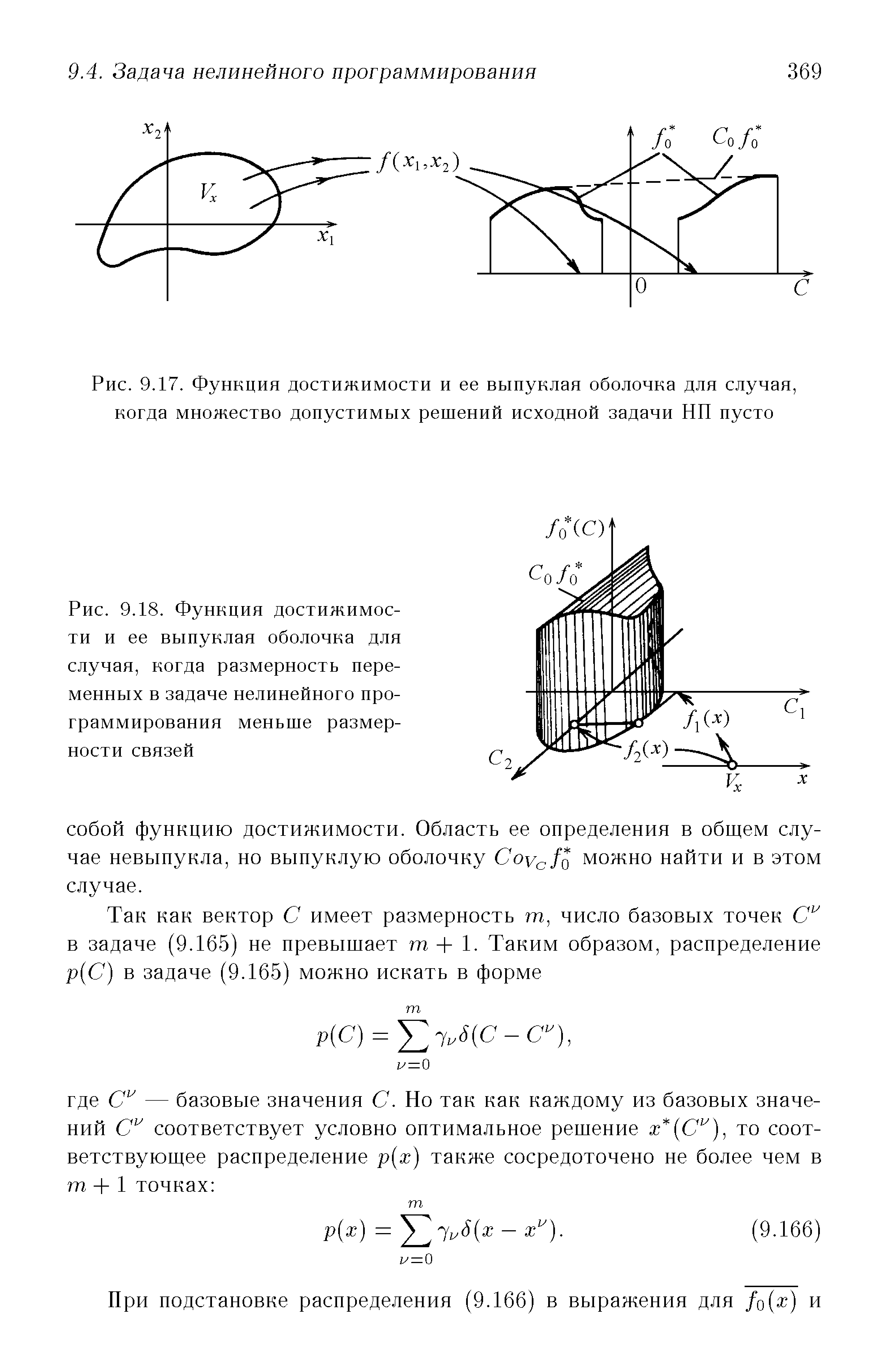 |
Пусть T=[TO, TI] — заданный отрезок времени. Состояние системы в момент <ет определяется точкой x(t) Rn. Управление системой обеспечивается r-мерной вектор-функцией u(t). Множество допустимых управлений U представляет собой заданное ограниченное множество пространства Lzr(t) суммируемых с квадратом на отрезке т / -мерных вектор-функций. Состояние системы х меняется в соответствии с выбранным управлением . Вектор состояния системы x(t, и, хц, d) для любых et/ и tst является решением задачи Коши [c.164]
Следствие 4.1. Пусть D и DZ множества допустимых решающих правил задач классов (2.1) — (2.3) и (4.1) — (4.3), отвечающих одним и тем же функциям tyh(( >h, xh) и множествам Gi°, a [c.199]
Пусть элементы матриц Л - — детерминированные величины. В этом случае область Кг определения допустимых решающих правил окажется выпуклым многогранным множеством. [c.239]
Этап 2. Выбираются критериальные ограничения. Конструктор просматривает таблицу испытаний по каждому критерию, назначает ограничения на Ф . Нужно помнить, что если Ф брать неоправданно малым, то множество допустимых точек может оказаться пустым. [c.215]
Пусть в результате выполнения (f — 1) шагов проект перешел в состояние (гг- ь qt-i), тогда множество допустимых управляющих воздействий на i-м шаге определяется следующим образом [c.219]
Плоскость (о2, ) называют критериальной. Меняя портфель, то есть меняя вектор х, получают различные оценки, а для них разные точки на критериальной плоскости. Множество всех оценок (то есть множество пар (а2, Е), а не множество портфелей) допустимых портфелей называют критериальным множеством. Если критериальное множество не сводится к одной точке, то возникает проблема выбора. Пусть По — некоторый портфель, а Со = (о2, ЕО) — оценка для П0. [c.468]
В прямой задаче допустимое множество не цусто, а целевая на этом множестве не ограничена сверху. При этом у двойственной задачи будет пустое допустимое множество. [c.203]
Пусть задано множество М допустимых (в рамках сущест- [c.137]
Пусть X— решение, Хе Дх, Дх — допустимое множество решений. Критерии оценки решений задаются п скалярными функциями У, У2> ---гУп образующими вектор у, причем Х- Y = F(x). Функционал F(x) может быть задан аналитически, статистически или эвристически. При этом необходимо найти оптимальное решение [c.107]
Пусть хозяин некоторого производства (prin ipal) хочет найти оптимальную схему стимулирования своего работника (agent)46. Предполагаем, что выпуск или доход предприятия у = у(х есть возрастающая функция от усилий работника х е X, выбираемых из его допустимого множества X, и от случайного фактора G 5. Задача хозяина — максимизировать математическое ожидание своей выгоды на множестве возможных контрактов. Контракт R(.) — это плата, получаемая работником, как функция от некоторого набора наблюдаемых хозяином переменных. Такими переменными могут быть у, х, или s, где s — прочие наблюдаемые начальником сигналы, т. е. случайные переменные, распределение которых зависит статистически от х и/или . В наихудшей для начальника ситуации можно делать контракт зависимым только от выпуска у, поскольку ни действия х, ни случайный фактор не наблюдаются начальником R = R(y). В общей постановке известно также распределение фактора [c.68]
Пусть допустимое потребительское множество Х= жеМ+ xix2+xi 1 , потребитель имеет фиксированный доход R > 0, цены на товары задаются вектором реМ++. Изобразите графически бюджетное множество потребителя при разных значениях (р,Д). Является ли оно выпуклым Замкнутым Ограниченным При каких значениях (p,R) бюджетное множество пусто [c.54]
Пусть /, 7, U, 9— множество соответственно типов резервуаров, размеров емкостей, видов хранимых нефтепродуктов и допустимых оборачивавмостей. Обозначим через Vw резервную емкость типа w, размера V, используемую для хранения нефтепродукта вида г с оборачиваемостью ko Кгт° —капитальные затраты по отдельному резервуару G ° —годовые потери нефтепродукта r-го вида яри о-й оборачиваемости в результате испарения из резервуара типа w размера V. [c.145]
А Пусть множество допустимых векторов Y— конечно и имеет вид Y = у у2,..., yN). Для каждого у е Квведем конечное множество [c.144]
Заметим, что множество допустимых решений задачи нелинейного программирования (9.81) может быть пусто, т.е. внутри Vx, например, нет элементов, для которых fi(x) равнялись бы нулю. При этом функция /о (С) не определена в точке С = 0. Однако для построения ova/Q множество V дополняют до его выпуклой оболочки, и на дополнительных участках / (С) считают достаточно малой. При этом oy /Q на этих участках определена. На рис. 9.17 приведен пример функции достижимости и ее выпуклой оболочки. Решение исходной задачи отсутствует, так как для любого х Е Vx функция / не равна нулю. Усредненная задача имеет решение, которому соответствует значение целевой функции, равное " v /g(0). [c.368]
Процесс представляется в виде дерева с XQ — начальным состоянием и д ет. .. ю — состоянием, достигнутым системой в момент времени t=k из состояния Хо через последовательность 0ь. .., ,. .., fho. Здесь ft1, , Оп = / ш<и, где U — множество допустимых управлений (входов). Пусть имеется N целей Qi,. . ., Q и N ограничений LO,. . ., LJV-I. Стратегия, обеспечивающая нерасплывчатое решение R, представляется последовательностью ий, и, . .. [c.87]
