Таким образом, все значения оси ординат, находящиеся в зоне менее 1 ПДК, не представляют опасности (функция принадлежности равна нулю), а в зоне более 10 ПДК - несут максимальную опасность (функция принадлежности равна единице). Интервал значений от 1 до 10 ПДК выражается линейной зависимостью. [c.6]
Поскольку для большого числа объединений не была установлена линейная зависимость между фактическим удельным расходом и приведенными выше факторами, то наряду с линейной моделью для всех объединений была опробована многофакторная степенная модель, которая описывается так называемой функцией Кобба— Дугласа ( 2 ) [c.52]
Линейная производственная функция. Предполагается линейная зависимость выпуска от затрат [c.99]
Наиболее часто рекомендуется пользоваться следующими функциями прямая зависимость, полином с целочисленными степенями, степенная функция, показательная функция. В настоящей работе рассматриваются гипотезы о наличии связи между себестоимостью добычи нефти и попутного газа и факторами в форме множественной линейной, полиномов трех первых степеней, мультипликативная функция Кобба — Дугласа и кинетическая производственная функция. [c.79]
Нахождение оптимального варианта возможно для линейной зависимости или выпуклой функции 5,- 3-= =f(ti-j), которая методом кусочно-линейной аппроксимации сводится к решению линейной задачи. [c.117]
Корреляционная зависимость в отличие от функциональной является неполной, проявляется лишь в среднем и только в массе наблюдений. При корреляционной связи изменению аргумента соответствует несколько значений функций. В зависимости от количества отобранных факторов различают парные и многофакторные модели различного вида линейные, степенные, логарифмические. В практике прогнозирования наибольшее распространение получили линейные модели вида [c.129]
Рассматривает линейную зависимость между зависимой и независимой переменными. Описывается в форме Y = а + ЬХ, в то время как нелинейная регрессия предполагает нелинейную зависимость, например, экспоненциальную и квадратическую функции. См. Регрессионный анализ. [c.462]
Хотя первоначальная продажная цена нового товара является сравнительно высокой (в среднем на 8,5—10,0% выше, чем при пробной продаже), на этой стадии она не подлежит снижению. По своим характеристикам цена максимальна и эластична, то есть она имеет предельный рассчитываемый уровень, при котором обеспечивается сбыт, а количественные соотношения спроса и продажной цены отвечают линейным зависимостям функции эластичности. [c.127]
Если функцию регрессии можно удовлетворительным образом аппроксимировать линейной зависимостью, то такая регрессия [c.92]
На практике может оказаться, что функцию регрессии невозможно описать удовлетворительным образом ни линейной зависимостью, ни любой из перечисленных в предыдущем параграфе нелинейных функций. Тогда стоит попытаться аппроксимировать ее комбинацией этих функций. Делается это следующим образом [c.130]
Для степенной функции ух = а х6 /и = 1и формула F-крите-рия примет тот же вид, что и при линейной зависимости [c.85]
Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены. В общем виде для совокупности обследуемых уравнение регрессии имеет вид [c.141]
Такая обратная зависимость также является убывающей максимальная цена при покупке большего количества того же самого товара всегда снижается. Связь прямой и обратной функций спроса может быть наглядно продемонстрирована на примере линейной зависимости [c.39]
Такая обратная зависимость также является возрастающей минимальная цена при производстве и продаже большего количества того же самого товара всегда повышается, прежде всего из-за возрастания альтернативных издержек, о котором говорилось в предыдущей главе. Связь прямой и обратной функций предложения также может быть наглядно продемонстрирована на примере линейной зависимости [c.43]
Подбор функций (моделей тренда), их использование и верификация результатов осуществляются известными методами математической статистики. Наиболее широкое применение при прогнозировании электропотребления нашли линейная, экспоненциальная и логистическая модели трендов, т.е. функции электропотребления от параметра времени. Для линейной зависимости характерны снижающиеся темпы роста электропотребления, для экспоненциальной - постоянные, а для логистической - переменные. Метод экстраполяции применяется главным образом для краткосрочного прогнозирования. [c.198]
См. также Векторное (линейное) пространство, Линейная зависимость векторов, Линейная комбинация векторов, Линейная модель, Линейная оболочка, Линейная форма, Линейная система, Линейная функция, Линейность в экономике. [c.169]
Слово "программирование" объясняется здесь тем, что неизвестные переменные, которые отыскиваются в процессе решения задачи, обычно в совокупности определяют программу план) работы некоторого экономического объекта. Слово "линейное" отражает факт линейной зависимости между переменными. При этом, как указано, задача обязательно имеет экстремальный характер, т.е. состоит в отыскании экстремума (максимума или минимума) целевой функции. [c.170]
ЛИНЕЙНЫЕ ЗАВИСИМОСТИ, СООТНОШЕНИЯ - экономико-математические модели в виде уравнений, в которых экономические величины (аргумент и функция) связаны между собой линейным образом. Простейший пример линейной зависимости у = kx. Графически линейная зависимость изображается прямой линией. [c.163]
Если линейное соотношение, действительно, справедливо и эмпирические данные (ti, yO, (t2, у2),. .., (t.,, у ) измерены точно, то полученная система совместна, ранг матрицы системы равен двум (число неизвестных) и значения коэффициентов линейной зависимости можно найти из первых двух уравнений системы. На практике такая ситуация невозможна — эмпирические данные по своей природе всегда содержат ошибку, а линейная модель лишь приближенно описывает реальные связи величин. Следовательно, система несовместна и ее нормальное обобщенное решение позволяет найти наилучшие приближенные значения коэффициентов линейной функции, поскольку в этом случае невязка минимальна. Построенному таким образом решению можно дать геометрическую [c.87]
В 1.4 мы ограничились линейной функцией, характеризующей зависимость темпа выхода загрязнений в окружающую среду г от темпа подачи загрязнений на очистные сооружения [c.72]
Нетрудно показать, что для линейной зависимости (7.54) потока закупок от разности цен этот поток при р = р (PQ) также является гауссовым случайным процессом с корреляционной функцией [c.258]
В общем случае m условий равенства (9.68) и (9.70) означают, что в точке ж градиенты целевой функции и функций /а- линейно зависимы, т.е. найдется такой вектор Л с составляющими Аа-, что [c.332]
Условие стационарности любой из функций Д на множестве, определяемом остальными условиями задачи, может быть записано (аналогично условиям оптимальности) как условие линейной зависимости [c.333]
Однако экономическая теория и практика свидетельствуют, что величина производственных затрат существенно зависит от объемов производства продукции, т. е. является функцией от них. Как правило, концентрация производства приводит к снижению удельных производственных затрат вследствие экономии на накладных расходах и т. п. Соответственно правомерно определять общую величину производственных затрат не как произведение единого норматива затрат на объем производства (линейная зависимость), а как произведение переменного норматива, представляющего собой функцию от размеров производства, на объем производства (нелинейная зависимость). [c.149]
Отсюда видно, что при данных уи и yv величина у представляет собой линейную функцию относительно числа детей. Это же подтверждается и графическим расположением точек (xi,yi). Второй этап. Определим неизвестные параметры а и 6 линейной зависимости [c.326]
В дальнейшем нам понадобятся понятия линейной зависимости и независимости функций. [c.374]
Две функции yi и уч называются линейно зависимыми, если [c.374]
Например, функции у = ж, уч = Зж линейно зависимы, а функции т/1 = ж, т/2 = х + 1 линейно независимы. [c.374]
От того, линейно зависимы или линейно независимы функции yi и у2, зависит ответ на вопрос является ли функция у = = С у + Сч уч общим решением уравнения (18.8) [c.374]
При отыскании общего и частного решений уравнений (18.21) и (18.22) важную роль играет понятие линейной зависимости и независимости функций yi(x), У2(х),. .., уп(х]. [c.398]
Определение линейной зависимости и независимости для двух функций у и у2 было дано на с. 374. Приведем более общее определение, пригодное для любого конечного числа функций. [c.398]
Функции т/1 (ж), уз(х),. .., уп(х] называют линейно зависимыми в интервале (а, 6), если существуют постоянные числа //i, не все равные нулю, такие, что [c.398]
Как отмечалось, функции полезности, связанные друг с другом возрастающей линейной зависимостью v(w) = а + bu(w), b > 0, описывают одну и ту же систему предпочтений субъекта. Так как и (w) = bit (w) и v"(w) = bu"(w), абсолютные меры Эрроу—Пратта для функций u(w) и v(w) совпадают это позволяет утверждать, что мера Эрроу-Пратта выражает свойства предпочтений индивида, а не представляющей их функции полезности. То же относится и к относительной мере Эрроу— Пратта [c.660]
Мы могли бы получить тот же результат, всего лишь взглянув на эти две функции. Мы знаем, что изменение Y будет равно трехкратному изменению X, таким образом, ДУ/ДЛ" равно 3. Очевидно, что поскольку функция линейна, то наклон графика, или скорость изменения У в зависимости от изменения X, всегда равен 3, таким образом, ДУ/Д постоянно. Кроме того, свободный член первой функции (12) не имеет никакого влияния на наклон прямой, а влияет только на ее расположение. Таким образом, свободный член не влияет на скорость изменения У. [c.129]
Структура оптимизационной модели состоит из целевой функции, области допустимых решений и системы ограничений, определяющих эту область. Целевая функция в самом общем виде, в свою очередь, также состоит из трех элементов управляемых переменных, неуправляемых переменных и формы функции (вида зависимости между ними). Если все функции, описывающие некоторую экономическую ситуацию линейны, то имеем задачу линейного программирования, к которой и будет сведена задача игры с природой о нахождении оптимального ассортимента продукции, выпускаемой швейным производством. [c.23]
| Рисунок 12. Выявление нелинейной составляющей функции у = 1 Ох + зш(л") + 0.5// после вычитания линейной зависимости у = 1 O.Y . ( Здесь г) - гауссовый случайный шум) | 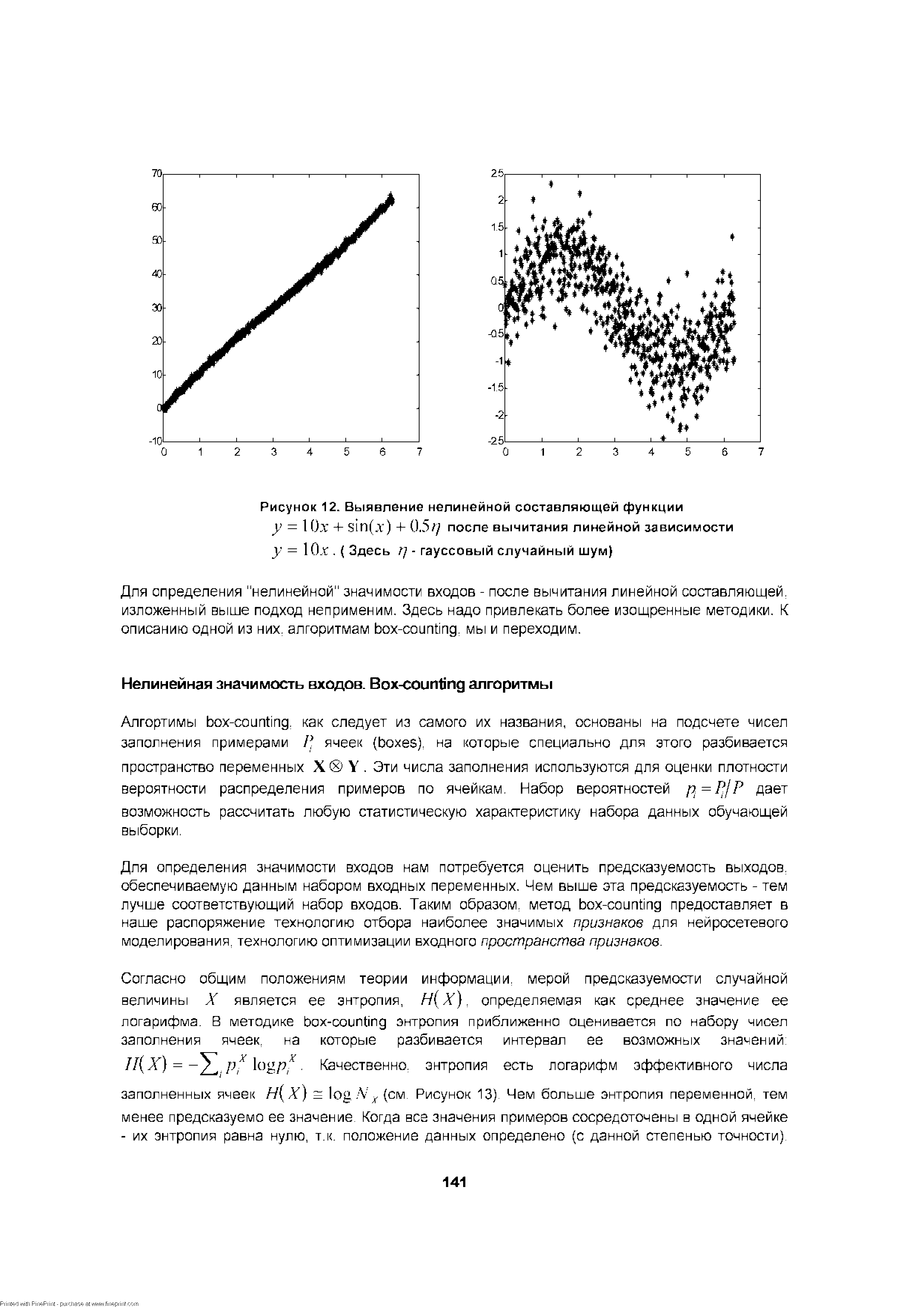 |
Таким образом, здесь представлена общая задача математического программирования с оговорками как ограничения, так и целевая функция линейные, а искомые переменные неотрицательные. Обозначения можно трактовать следующим образом Ъ. — количество ресурса вида i m — количество видов этих ресурсов а.. — норма расхода ресурса вида i на единицу продукции видау х. — количество продукции вида j, причем количество таких видов —п с. — доход (или другой выигрыш) от единицы этой продукции, а в случае задачи на минимум — затраты на единицу продукции нумерация ресурсов разделена на три части от 1 до ту от т1 + 1 до т2 и от т1 + 1 до т в зависимости от того, какие ставятся ограничения на расходование этих ресурсов в первом случае — "не больше", во втором — "столько же", в третьем — "не меньше" Z— в случае максимизации, напр., объем продукции или дохода, в случае же минимизации — себестоимость, расход сырья и т.п. Добавим еще одно обозначение, оно появится несколько ниже v. — оптимальная оценка г -го ресурса. [c.170]
В теореме 5 рассмотрен случай, когда каждая строка матрица R является линейной комбинацией строк матрицы X, при этом r(X R ) = г(Х ) и класс оцениваемых функций остается прежним. В этом параграфе рассматривается обратная ситуация, когда строки матрицы R не являются линейно зависимыми от строк матрицы X, т. е. o (Rf) Псо1(Х ) = 0 . Как будет видно, наилучшая аффинная несмещенная оценка имеет в этом случае довольно простой вид. [c.341]
В общем случае, из Я [х, ф, и ] >Я [я, ф, и] не следует (Ни [х, ф, и], и —и) > 0, понижение F0 с ростом s не гарантируется (отрицательные значения s могут быть запрещены условием и (t, s) U). Однако в очень распространенной ситуации, при линейной зависимости всех функций / (х, и) от и, (Ни, и —и) > О, и метод оказывается сходящимся. В общем случае сходимости может не быть при сколь угодно хорошем начальном приближении. Конструкция (45) с точки зрения сходимости более естественна и логична ведь глобальный характер (по и ( U) уравнения принципа максимума связан с использованием конечных вариаций на множествах малой меры, и конструкция (45) в отличие от (42), это учитывает. В 6 была получена формула для приращения функционала, вызванного конечным изменением управления на множестве М, малой меры р,=шезМ, [c.154]
Начнем анализ ARIMA с рассмотрения авторегрессионного процесса. Авторегрессионным называется процесс, при котором значение ряда находится в линейной зависимости от предыдущих значений. Например, если текущее наблюдаемое значение является функцией всего лишь одного значения, непосредственно предшествующего наблюдению, т.е. процесс зависит всего лишь от одного значения рассматриваемой переменной, то процесс называется авторегрессионным процессом первого порядка и обозначается AR(1). Это можно обобщить следующим образом если анализируемый динамический процесс зависит от значений, отстоящих от 1 до п временных лагов назад, то это авторегрессионный процесс порядка и, т.е. AR(w). Например, процесс AR(3) можно отобразить следующим образом [c.321]
