Сглаживание линейное 182 Сертификаты качества 152 Система замкнутая 92 — контроля, статистическая [c.252]
Экспоненциально сглаживать на самом деле можно не только сам но и коэффициенты трендов, линейного или экспоненциального, циенты сезонности и т.п. Параметр сглаживания а в модели (1) также может быть не постоянной, а изменяющейся величиной (соответствующие методы называют методами адаптивного прогнозирования). [c.32]
Изучение тенденций развития динамики себестоимости добычи нефти, статей затрат и факторов, оказывающих решающее влияние на уровень и динамику этих показателей, свидетельствует о том, что моделирование их можно выполнить при использовании прежде всего таких функций времени (трендов), которые решаются методом наименьших квадратов (линейные, параболические, показательные, логарифмические), а также с применением методов экспоненциального сглаживания, гармонических весов и т. д. [c.102]
Планируемые в рамках управленческого учета расходы, в первую очередь, должны применяться для контроля издержек ответственным персоналом с использованием при этом методов составления планов-счетов с учетом переменных издержек. На последующих этапах, которые будут рассматриваться ниже, планируемые расходы собирают для разработки ставки накладных расходов, подлежащей использованию при расчете себестоимости продукции и при определении дохода. В процессе такого подведения итогов некоторые мешающие анализу особенности поведения отдельных статей расходов можно сгладить с целью получения линейно-переменных зависимостей. На данном уровне сглаживание представляет собой функцию учета, которая не имеет отношения к контролю издержек. Однако сами планы-сметы, составленные с учетом переменных издержек, которые будут применяться на оперативном уровне, должны быть как можно реальнее при описании ожидаемого поведения конкретных статей издержек. [c.181]
Как видно из графика на рис. 6.3, имеются существенные колебания показателей объема продаж. Однако отмечается видимая тенденция к увеличению объема продаж, и соответствующий тренд можно выделить с помощью методов регрессии. Линия регрессии показана на графике (рис. 6.3). Из графика видно, что зависимость определена не столь четко, как в предыдущем примере. Так, коэффициент корреляции для этих данных будет значительно меньше по величине, и вообще может оказаться незначимым. Долговременный тренд может быть линейным или нелинейным. Эти данные трудно анализировать из-за сильных расхождений между соседними значениями. Часто, когда мы имеем дело с такого рода данными, необходимо сгладить колебания, и только потом можно сделать какой-либо имеющий смысл прогноз. Методы сглаживания данных временных рядов будут более подробно рассмотрены в последующих разделах. [c.188]
Большая часть примеров, приведенных в данной главе, описывают основные методы выработки моделей прогнозирования. Во-первых, в большинстве случаев предполагается, что тренд — линейный. Далее, стандартный метод выделения тренда основывается на скользящих средних, хотя мы осветили и другие методы, в том числе экспоненциального сглаживания. Во-вторых, при получении прогнозных данных использовались все имеющиеся значения, тогда как на практике это может быть не лучшим вариантом, особенно в тех случаях, когда собранные данные включают некоторые нетипичные значения. На примерах этого раздела мы рассмотрим некоторые вопросы, связанные с практическим прогнозированием, при этом предполагается, что вы уже достаточно хорошо усвоили основные методы прогнозирования, в частности знаете, как выделять тренд и выявлять и вычислять сезонные составляющие. [c.217]
Названные принципы лежат в основе конкретных методов ЭП. Методом прогнозирования называется способ исследования объекта прогнозирования, направленный на разработку прогнозов. Модель прогнозирования представляет собой модель исследуемого объекта, записанную в математической форме. Она должна позволить получить информацию о возможных состояниях объекта в будущем и (или) путях и сроках их осуществления. При построении прогнозной модели может быть использован один или несколько методов. Например, при построении линейной модели (уравнение прямой) могут быть использованы методы средних, двух точек, наименьших квадратов, экспоненциального сглаживания, гармонических весов, эволюции и др. [c.284]
Классическая задача сглаживания >и экстраполяции по минимуму дисперсии формулируется для случая /2=1. Целевой функционал R задачи — второй момент k = ku ошибок прогноза (с обратным знаком). Область допустимых планов определяется требованием несмещенности оценки m=mi = 0. Механизм сглаживания и прогноза предполагается линейным и определяется (в дискретном случае) набором весовых коэффициентов рц. Фильтрация по минимуму дисперсии целесообразна при отсутствии нерегулируемых ошибок. [c.41]
В литературе рассматриваются главным образом линейные методы сглаживания и прогноза. Линейные сглаживающие и упреждающие фильтры определяют сглаженную или упрежденную точку с помощью линейных операций над наблюденными до текущего момента значениями входного сигнала. Основной аргумент в пользу линейного сглаживания и линейного прогнозирования — относительная простота расчета и реализации соответствующих фильтров. Кроме того, можно показать, что для сглаживания гауссовского случайного процесса, гарантирующего минимальную дисперсию отклонения величины случайного сигнала от его истинною значения, линейный фильтр оказывается оптимальным. В общем случае, однако, отказ от требования линейности фильтров может повысить (IB ряде случаев существенно) качество сглаживания и прогноза. [c.301]
Введенные понятия позволяют строго поставить задачи сглаживания и прогноза и исследовать возможности синтеза линейных систем фильтрации и упреждения при различных критериях качества и различных ограничениях на статистические характеристики выходного сигнала. [c.306]
Различные постановки линейных задач сглаживания и прогноза можно приводить и обсуждать как в терминах случайных величин, так и в терминах функций веса. Соображения, приведенные в предыдущих пунктах, свидетельствуют об эквивалентности обоих подходов к задачам линейного сглаживания и прогнозирования. [c.306]
Результаты, не связанные с допущением о линейности сглаживания или прогноза, будут обсуждаться только в терминах случайных величин. [c.306]
В общем случае при постановке задачи о сглаживании и прогнозе случайных процессов исключение систематических ошибок экстраполяции (равенство нулю первого момента ошибок упреждения) не является обязательным и тем более единственным требованием рациональной фильтрации или рационального прогнозирования. Больше того, в ряде случаев целесообразно расширить область определения задачи и заменить требование о нулевых систематических ошибках ограничениями на их величину. Могут быть указаны и другие неравенства и логические соотношения, которым в тех или иных содержательных задачах фильтрации и прогноза должны удовлетворять, сглаженные или упрежденные точки. Например, может быть ограничена дисперсия или корреляционные моменты случайных величин, зависящих от г (/о + п) и (М- Можно указать содержательные постановки, в которых область определения задачи естественно задавать вероятностными или жесткими ограничениями. Таким образом, в общем случае ограничения задачи сглаживания и экстраполяции высекают в Я не линейное подпространство и не линейное многообразие, а некоторую выпуклую или невыпуклую область G. [c.309]
Задачи линейного сглаживания и экстраполяции по минимуму второго момента ошибок могут быть переписаны в терминах функции веса. Используя соотношение (2.1), можно переписать задачу (3.12) в виде [c.310]
Формулы (ЗЛО) и (4.2) имеют место как для линейных, так и для нелинейных методов сглаживания и упреждения. [c.312]
При некоторых технических реализациях линейных схем сглаживания механизм связи случайных процессов и описывается соотношением [c.312]
При некоторых дополнительных предположениях о характере процессов т) и и, следовательно, об их корреляционных функциях уравнения (4.4) и (4.6) могут быть решены. Полученные при этом функции веса определяют схему линейного фильтра или линейную вычислительную процедуру сглаживания и прогнозирования, оптимальную в смысле задачи (4.1). [c.313]
Заметим, что допущение о линейности сглаживания отнюдь не безобидно. В ряде случаев оно может существенно снизить достижимое качество фильтрации. Последнее утверждение иллюстрируется следующим примером. [c.314]
Как видим, при немалых п оптимальное линейное сглаживание явно менее эффективно абсолютно оптимального нелинейного сглаживания [c.315]
Сглаживание по экспоненте Прогнозные показатели получаются в результате сглаживания, усреднения, ряда прошлых показателей по линейному или экспоненциальному типу [c.253]
Метод двойного сглаживания Брауна Как показал Браун [3], в условиях линейного тренда простое экс- [c.31]
| Рис. 2.6. Обобщенная номограмма вычисления прогноза на т моментов времени вперед в случае линейно-аддитивного тренда (метод двойного сглаживания Брауна) | 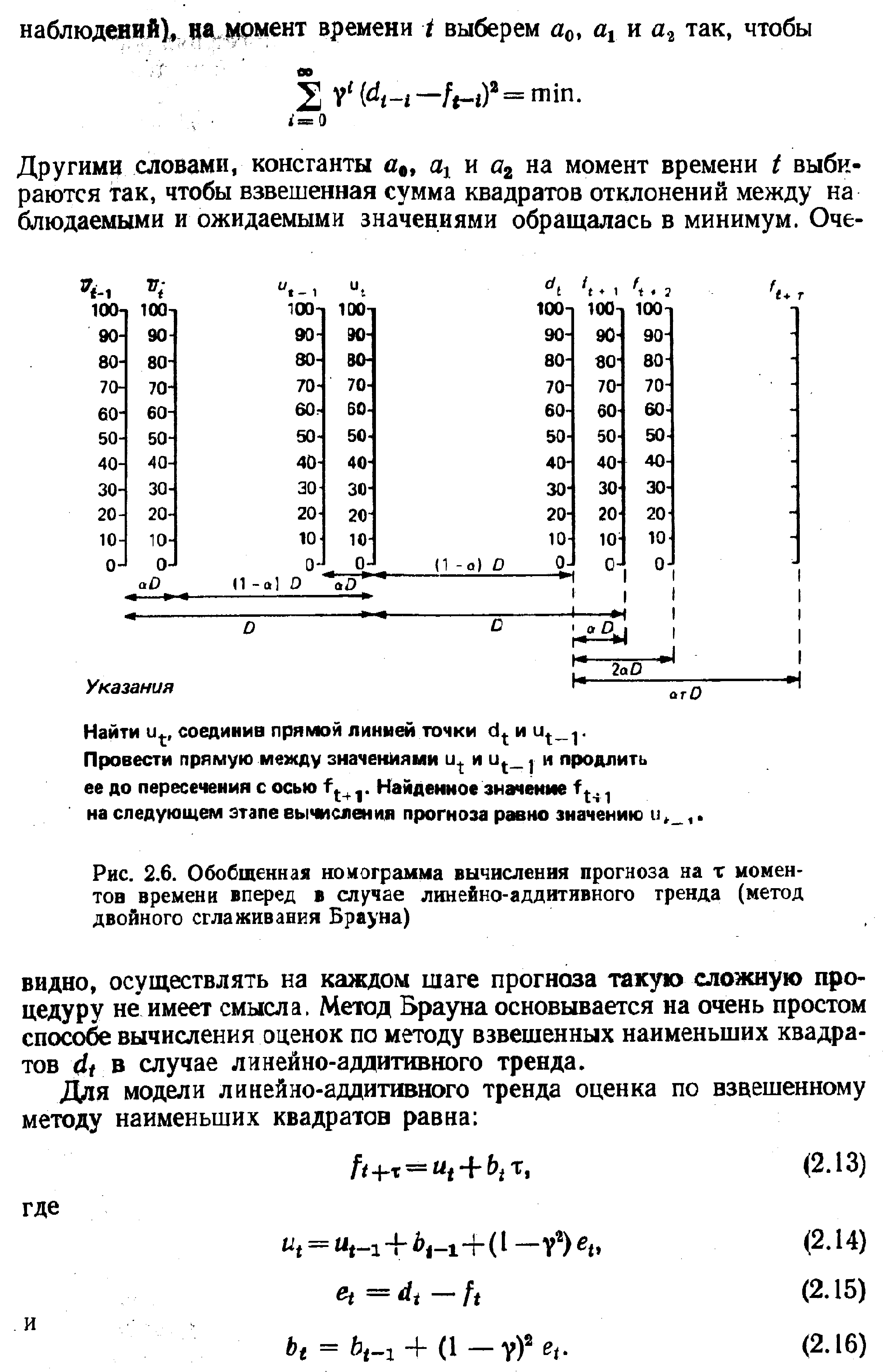 |
Метод двойного сглаживания Брауна. В условиях линейного тренда экспоненциально взвешенное среднее (7.5) всегда меньше линейного тренда на величину [c.126]
Метод адаптивного сглаживания Брауна. Согласно второму методу Брауна, предполагается, что если ряд значений спроса можно описать некоторой моделью, то желательно применить регрессионный анализ на основе взвешенной регрессии, т. е. большее внимание необходимо уделять той информации, которая поступает позже. Данный метод основывается на простом способе вычисления оценок по методу минимизации взвешенной суммы квадратов ошибок прогноза в случае линейно-аддитивного тренда. Оценка по взвешенному методу наименьших квадратов равна [c.127]
Наименьшую ошибку модели экспоненциального сглаживания с тремя параметрами дает следующее сочетание a = 0,44 b = 0,42 g = 0,67. Начальные условия модели выбраны следующие для сглаживания ряда — среднее за первый год, т. е. (300 + 320 + 325 + 295)/4 = 310 для учета тренда — коэффициент линейной модели, соответствующий наклону тренда, подобранного по данным первого года, т. е. (-1) для учета сезонности в первом квартале 300/310 = 0,968, во втором квар- [c.442]
Чаще всего для сглаживания применяют линейную зависимость. Тогда формулы сглаживания для групп из трех точек имеют вид [c.166]
Сглаживание (даже в простом линейном варианте) является во многих случаях эффективным средством выявления тренда при на- [c.166]
Рассмотрим применение метода экспоненциального сглаживания для двух наиболее употребительных случаев, когда тренд описывается линейной функцией и параболой. [c.172]
Прогноз с использованием экспоненциального сглаживания. Прогноз осуществляется по линейным и параболическим зависимостям. Параметры моделей рассчитываются по формулам, предложенным Брауном. Выбор параметра сглаживания ос производится в пределах от 0,1 до 0,9 с шагом 0,1. При комбинированном прогнозе выбор параметра производится по формуле а = 2/(N +1), где N - число точек временного ряда. [c.186]
Например, требуется получить прогноз объемов продаж на следующий месяц. Имеется сеть магазинов розничной торговли. Первым шагом будет сбор истории продаж в каждом магазине и объединение ее в общую выборку данных. Следующим шагом будет предобработка собранных данных их группировка по месяцам, сглаживание кривой продаж, устранение факторов, слабо влияющих на объемы продаж. Далее следует построить модель зависимости объемов продаж от выбранных факторов. Это можно сделать с помощью линейной регрессии или нейронных сетей. Имея такую модель, можно получить прогноз, подав на вход модели историю продаж. Зная прогнозное значение, его можно использовать, например, в приложениях оптимизации для лучшего размещения товара на складе. [c.11]
Для периодов времени, достаточно удаленных от краев временного ряда, данный метод может быть представлен как взвешенное скользящее среднее с симметричными весами (некоторые из них могут быть отрицательными). Таким образом, его можно рассматривать как линейный фильтр, который в силу симметричности весов не порождает фазового сдвига. Свойства такого фильтра могут быть описаны передаточной функцией. В идеале для линейного фильтра, соответствующего методу сглаживания, хотелось бы иметь ступенчатую передаточную функцию, которая бы без искажений пропускала все низкочастотные составляющие вплоть до некоторой заданной пороговой частоты и полностью гасила бы все составляющие, соответствующие более высоким частотам. Однако известно, что такой идеальный фильтр должен иметь бесконечную длину. Поэтому используемые на практике фильтры имеют передаточные функции, отличающиеся от идеальной. В частности, они имеют близкие к единице значения в области низких частот и близкие к нулю значения коэффициента передачи в области высоких частот. Эти полосы пропускания и непропускания разделяет сопрягающий участок. [c.224]
Сглаживание временного ряда 412 Система линейных алгебраических [c.463]
Каждый метод сглаживания и прогнозирования приводит в соответствие значениям случайной функции (/) на интервале (to— T, to случайную величину t,(t0) — оценку сглаженного или упрежденного значения случайной величины r (to + tu). Здесь 4 — текущий момент, Т — наблюдательное время, tn — интервал прогнозирования — упредительное время. Если связь между (4) и значениями i (i) на (4 — Т, to) линейна, говорят, что метод сглаживания или упреждения линеен, а соответствующее устройство, реализующее усреднение или прогноз, — линейный фильтр. В общем случае связь между (4) и ( ) может быть нелинейной и t,(tQ) является элементом некоторого множества N (U, Т), порожденного значениями ( ) на (to — Т, to). [c.302]
Меняя механизм фильтрации и прогнозирования (функцию веса P(to, т) в линейном случае), можно в широких пределах изменять ста1-тистические характеристики случайных величин , а следовательно, и погрешность б-прогноза. Строго говоря, случайные величины б следовало бы называть регулируемыми ошибками прогноза. В задачах управления ошибки прогноза складываются из ошибок вида (3.1), где определяется выбранным механизмом сглаживания и упреждения, и нерегулируемых ошибок прогноза — случайных погрешностей экстраполяции, не зависящих от выбора схемы прогнозирования. [c.307]
Это интегральное уравнение, точнее, частный его случай, относящийся к стационарным случайным процессам и бесконечному наблюдательному времени, называется уравнением Винера — Хопфа. Решение его, принадлежащее области iQp, определяет оптимальную функцию веса линейного фильтра, который обеспечивает сглаживание (при /п = 0) и экстраполяцию (при п>0) по минимуму второго момента ошибок в соответствии с задачей (4.1). [c.312]
Заметим, что уравнения Винера — Хопфа вида (4.4) и (4.6) справедливы и при менее жестких условиях, когда область Q — не Линейное пространство, а линейное многообразие в гильбертовом пространстве Я, определяемом заданным законом изменения математического ожидания t(t)—h(t). Действительно, в этом случае t является решением задачи сглаживания или упреждения по минимуму второго момента ошибок тогда и только тогда, если выполняется равенство (3.8) или, что то же самое, соотношение (3.9). Для линейных фильтров, когда и ( ) свя заны формулой (2.1), соотношение (3.9) может быть представлено в виде [c.313]
Откажемся теперь от требования линейности механизма сглаживания или прогнозирования и предположим, что линейное простран- [c.313]
Для выбора правильной прогностической модели первоначально необходимо выбрать некоторые характеристики анализируемого ряда данных. Использование сложной модели типа сезонно-аддитивной модели Холта—Винтера (описанной на с. 37—39), если данные стационарны, нецелесообразно, тем более, что применение простой модели экспоненциального сглаживания при меньших затратах дает те же результаты. Наоборот, если ряд наблюдений содержит линейный тренд, на который наложены сезонные колебания, то применение модели простого экспоненциального сглаживания будет, очевидно, неадекватным. [c.65]
Хольт (Holt С. С.) 1957 Разработал двухпара-метрическую модель экспоненциального сглаживания с учетом линейного тренда, меняющегося со временем 1 ) сглаживание данных а( = ау( + (1 - a)(at 1 + bt- 1) 2) сглаживание тренда Ь, = j3(at-a,-,) + (1 - /7)b(-i 3) прогноз на период f + /
Существует огромное разнообразие адаптивных скользящих средних и других сложных методов сглаживания, разработанных в целях минимизации запаздывания. Одна из таких методик основывается на стандартных способах предсказания временных серий. По Маллой (Mulloy, 1994) используется линейная рекурсивная схема с множественными скользящими средними. Когда уровень движения на рынке достаточен для отключения фильтра, запаздывание исчезает впрочем, фильтры имеют тенденцию недостаточно сглаживать данные и работают заметно хуже, когда рынок отклоняется от настроек этих фильтров. Чанд ( hande, 1992) [c.132]
Уинтерса (экспоненциального сглаживания с мультипликативной сезонностью и линейным ростом) [c.83]
Используя данные таблиц Приложения Б, построить прогноз с использованием модели Уинтерса (экспоненциального сглаживания с мультипликативной сезонностью и линейным ростом). [c.90]
Требуется по модели экспоненциального сглаживания с аддитивной сезонностью и линейным ростом (модель Тейла-Вейджа) определить расчетные значения х и прогноз при t-9, приняв период [c.91]
