Частный случай линейных ограничений представляет собой ситуация, когда один или несколько параметров задаются точно. Предположим, что подобная задача возникла в случае всего двух объясняющих переменных и мы знаем заранее значение (32 = с. Работая с уравнением в отклонениях от средних, мы можем выразить этот известный параметр в виде линейного ограничения [c.159]
Иногда при построении уравнений множественной регрессии по временным рядам автокорреляция возникает в отклонениях фактических значений зависимой переменной от расчетных, выравненных по уравнению регрессии. [c.70]
Это означает, что в среднем за период отклонение себестоимости от тренда было противоположно по знаку и составляло 0,124 отклонения урожайности от своего тренда. Если, например, урожайность в 1993 г. окажется на 20 ц/га ниже уровня тренда для этого года, составляющего 119,9 + 3,81 10 = 158 ц/га, то себестоимость надо ожидать на-20 (-0,124) = 2,48 руб. за 1 ц выше уровня тренда, который для 1993 г. равен 31,2 руб. за 1 ц, т. е., учитывая и тренды, и предполагаемый плохой урожай в 1993 г., себестоимость картофеля составила бы 31,2 + 2,48 = 33,66 руб./ц. Естественно, что этот прогноз всего лишь пример, как пользоваться уравнением регрессии отклонений от тренда. В нашем случае метеорология не дает оснований для прогноза урожайности, а сильнейшая инфляция делает вообще невозможным любой прогноз себестоимости без использования дефлятора (см. гл. 10). [c.365]
Иначе обстоит дело, когда преобразования уравнения в линейную форму связаны с зависимой переменной. В этом случае линейный коэффициент корреляции по преобразованным значениям признаков дает лишь приближенную оценку тесноты связи и численно не совпадает с индексом корреляции. Так, для степенной функции yx = a-xb после перехода к логарифмически линейному уравнению lny=lna + b-lnx может быть найден линейный коэффициент корреляции не для фактических значений переменных хпу,а для их логарифмов, т. е. rln)inx. Соответственно квадрат его значения будет характеризовать отношение факторной суммы квадратов отклонений к общей, но не для у, а для его логарифмов [c.83]
При обычном применении метода наименьших квадратов к уравнению линейной регрессии для переменных в отклонениях от средних уровней коэффициент регрессии Ь определяется по формуле [c.172]
Колебания рыночных цен. Примеры 1 и 2 применимы не только к колебаниям пружинного маятника. Рассмотренное дифференциальное уравнение применимо к любой системе, испытывающей колебания. Например, оно может быть интерпретировано и как уравнение колебаний отклонения рыночной цены товара от его естественной цены. Более точно эта интерпретация выглядит следующим образом. Пусть s(t) — отклонение рыночной цены от ее естественного значения в момент времени t (при s(t) = О рыночная цена в момент времени t совпадает с равновесной). Найдем уравнение отклонения рыночной цены от ее естественного состояния. Для этого предположим, что на рынке товаров действуют две силы, аналогичные силам упругости и сопротивления для пружинного маятника, которые условно назовем силой (тяготения) Смита и силой сохранения. Чтобы пояснить, что понимается под силой Смита, приведем две его цитаты [c.382]
Как видно, сумма отклонений имеет положительный знак и, следовательно, теоретическая линия регрессии систематически занижает расчетные величины моделируемого признака по сравнению с фактическими. Однако расчет параметров логарифмической функции по критерию (3) с использованием обычного метода решения системы уравнений в частных производных невозможен. Продифференцируем следующую форму по "а и и [c.84]
Оцененное уравнение в первую очередь должно описывать общий тренд (направление) изменения зависимой переменной Y. При этом необходимо иметь возможность рассчитать отклонения от этого тренда. [c.144]
Он характеризует долю вариации (разброса) зависимой переменной, объясненной с помощью данного уравнения. В качестве меры разброса зависимой переменной обычно используется ее дисперсия, а остаточная вариация может быть измерена как дисперсия отклонений вокруг линии регрессии. Если числитель и знаменатель вычитаемой из единицы дроби разделить на число наблюдений л, то получим, соответственно, выборочные оценки остаточной дисперсии и дисперсии зависимой переменной . Отношение остаточной и общей дисперсий представляет собой долю необъясненной дисперсии. Если же эту долю вычесть из единицы, то получим долю дисперсии зависимой переменной, объясненной с помощью регрессии. Иногда при расчете коэффициента детерминации для получения несмещенных оценок дисперсии в числителе и знаменателе вычитаемой из единицы дроби делается поправка на число степеней свободы тогда [c.313]
Записывая каждое уравнение, для простоты в отклонениях от средних значений (см. п. 2. 2), получаем следующую систему [c.224]
По существу, это — уравнение (13.3), записанное в отклонениях от индивидуальных средних по времени. В матричной форме соотношение (13.9) может быть записано так [c.364]
Ранее (п. 13.3) мы ввели понятие внутригрупповых оценок, перейдя от исходной регрессии (13.3) к регрессии в отклонениях от внутригрупповых средних (13.9). Преобразуем теперь уравнение (13.14), взяв средние значения по времени для каждой экономической единицы [c.369]
Установить связь можно с помощью группировки, но определить тесноту связи можно только путем составления уравнения корреляции и определения коэффициента (г) или индекса (р) корреляции. Уравнения корреляции являются по существу оттисками теоретической линии регрессии, в которой сумма квадратов отклонений фактических значений варьирующего признака от вычисленных по уравнению была бы наименьшей из всех возможных (на основе способа наименьших квадратов). [c.143]
Разработку норм по методу экстраполяции осуществляют в следующем порядке определяют фактические удельные показатели, соответствующие выбранному измерителю нормы, на конец каждого года в отчетном периоде троят график динамического ряда фактических удельных показателей в анализируемом (отчетном) периоде выявляют тенденцию изменения по годам отчетного периода показателей динамического ряда для оценки характера изменения удельных показателей в этом периоде осуществляют выравнивание динамического ряда с принятым измерителем нормы способом наименьших квадратов по прямолинейной или криволинейной зависимостям сущность способа наименьших квадратов состоит в нахождении наименьшей суммы квадратов отклонений фактических точек от линии выравнивания рассчитывают значения норм потребности в оборудовании по годам планового периода (или для последних лет пятилетних периодов) по уравнениям кривых различных математических функций. [c.167]
Установить связь можно с помощью группировки, но определить тесноту связи можно только составляя уравнения корреляции и определяя коэффициент корреляции г или индекс корреляции р. Построение уравнений корреляции является по существу оттисками теоретической линии регрессии, в которой сумма квадратов отклонений фактических значений варьирующего признака от вычисленных по уравнению была бы наименьшей из всех возможных (т. е. на основании способа наименьших квадратов). При линейной связи их теснота определяется коэффициентом- корреляции, рассчитываемым по формуле [c.23]
Так, например, по обсадным и бурильным трубам была взята база исходных данных за 1 967-1 97 9 гг., в основном динамические ряды фактических удельных расходов. В табл.1 для них приведены уравнения регрессии, результаты сопоставления прогнозов норм расхода с предложениями ВНИИОЭНГ)Г разработанными на основе расчетно— аналитического метода, и утвержденная норма. Сопоставление осуществлялось с учетом определения относительного отклонения между ними по формуле [c.25]
Метод наименьших квадратов. Согласно этому методу прямая затрат строится таким образом, чтобы сумма квадратов отклонений расстояний от всех точек до теоретической линии регрессии была бы минимальной. Для установления зависимости между затратами и объемом и определения суммы затрат используют методы математической статистики, в частности метод наименьших квадратов (МНК). Функция Y = а + ЬХ, отражающая связь между зависимой и независимой переменными, называется уравнением регрессии, а и b -параметры уравнения. [c.98]
Математический аппарат этого метода описан достаточно подробно в литературе. Метод наименьших квадратов заключается в том, что сумма квадратов отклонений фактических значений функции Y от значений, найденных по уравнению регрессии, должна быть наименьшей. [c.98]
В чем же тогда заключается целесообразность анализа с помощью уравнений Внутри относительно строгих границ анализ с помощью уравнений даст вам ориентиры и ключевые решения, особенно при определении возможных путей к лучшей или худшей деятельности и при поиске важных отклонений от любых средних или применяемых в определенных областях норм. Именно при интерпретации таких [c.66]
Сравните результаты уравнения с результатами других организаций в вашей отрасли и с соответствующими показателями во всей промышленности. Проанализируйте наиболее важные отклонения, если такие имеются, чтобы решить, почему у вас не так, как у других. [c.82]
Рассмотрим применение данного статистического инструментария для контроля сметы затрат. Контроль заключается в том, что затраты должны в конечном итоге соответствовать расчетам по уравнению регрессии, а значительные отклонения свидетельствуют о каких-то изменениях в производстве, которые должны быть рассмотрены. [c.206]
Коэффициенты регрессии показывают интенсивность влияния факторов на результативный показатель. Если проведена предварительная стандартизация факторных показателей, то Ь0 равняется среднему значению результативного показателя в совокупности. Коэффициенты Ь,, Ь2. .... Ьл показывают, на сколько единиц уровень результативного показателя отклоняется от своего среднего значения, если значения факторного показателя отклоняются от среднего, равного нулю, на одно стандартное отклонение. Таким образом, коэффициенты регрессии характеризуют степень значимости отдельных факторов для повышения уровня результативного показателя. Конкретные значения коэффициентов регрессии определяют по эмпирическим данным согласно методу наименьших квадратов (в результате решения систем нормальных уравнений). [c.282]
Для устранения автокорреляции можно использовать и другой прием, основанный на включении времени в уравнение множественной регрессии в качестве аргумента. Множественная регрессия с отклонениями от линейных тенденций точно эквивалентна прямому введению времени в управление регрессии. Это свойство впервые заметили Фриш и Boy [92]. [c.71]
Среди мер по устранению или уменьшению мультиколлинеарности отметим следующие 1) построение уравнений регрессии по отклонениям от тренда или конечным разностям 2) преобразование множества независимых переменных в несколько ортогональных множеств при помощи методов многомерного статистического анализа (факторного анализа или метода главных компонент) 3) исключение из рассмотрения одного или нескольких линейно связанных аргументов. [c.71]
Построение уравнения регрессии по отклонениям от линейных тенденций математически эквивалентно прямому введению фактора времени (t) в уравнение регрессии [47, 92]. Это справедливо также не только для линейных тенденций, но и для тенденций, выражающихся многочленами, и вообще для всех ортогональных функций [47, 92]. [c.73]
При классическом подходе пользуются методом наименьших квадратов, который основывается на предположении о независимости друг от друга отдельных наблюдений. Если данные наблюдения нанести на диаграмму, характеризующую рассеивание взаимосвязанных признаков, то линия, представляющая это уравнение, будет выбрана так, что сумма квадратов расстояний по вертикали между точками-и этой линией будет минимальной. Сущность метода наименьших квадратов заключается в том, что отыскиваются такие значения коэффициентов уравнения регрессии, при которых сумма квадратов отклонений фактических значений варьирующего признака от вычисленного по уравнению была бы наименьшей из всех возможных [c.321]
Метод экспоненциального сглаживания дает более точное приближение к исходному ряду, улавливая колебания цен. На рис. 9.4 приведены графики исходного и сглаженного ряда с помощью экспоненциального сглаживания. Динамическим рядам цен акций (как и ряду других фондовых инструментов) присущ ряд особенностей, которые могут определять специфику их анализа. Прежде всего это достаточно частые случаи резкого изменения тенденции цены (например, повышательный тренд, так называемый бычий, сменяется его противоположностью, так называемым медвежьим трендом). В этой ситуации возможно использование аналитической аппроксимации. Для оценки параметров уравнения, максимально точно описывающего динамику цен акций, используется метод наименьших квадратов, суть которого состоит в том, что подбирается такая аппроксимирующая кривая, при которой достигается минимум квадратов отклонений исходного ряда от теоретической кривой. [c.372]
Далее, подставляем в уравнение соответствующие значения os t, sin /, os 2t, sin 2t, os 3/, sin 3/ и т.д. В результате этих расчетов получаем выравненные уровни отклонений процентных ста- [c.617]
Вторая задача специфична для статистических связей, а первая разработана для функциональных связей и является общей. Основным методом решения задачи нахождения параметров уравнения связи является метод наименьших квадратов (МНК), разработанный К. Ф. Гауссом (1777-1855). Он состоит в минимизации суммы квадратов отклонений фактически измеренных значений зависимой переменной у от ее значений, вычисленных по уравнению связи с факторным признаком (многими признаками) х. [c.232]
| Рисунок 17.4. Объем реального частного потребления в США ( ONS, млрд.долл., 1982 г.) в 1971-1990 гг фактический и оцененный по уравнению регрессии. Отклонения от линии регрессии | 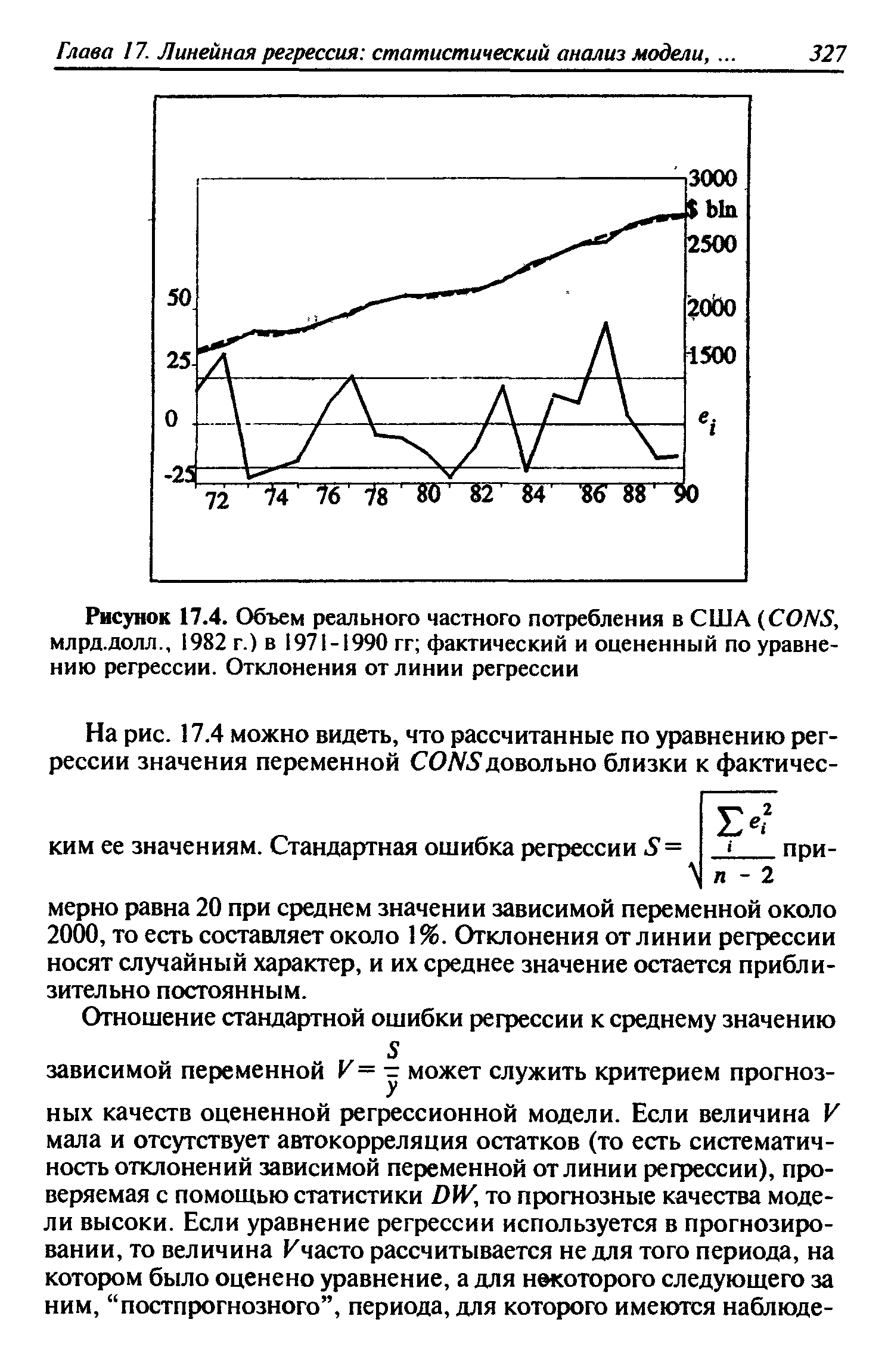 |
Изменение себестоимости добычи нефти и попутного газа во времени носит, в целом, криволинейный характер, хотя и неявно выраженный. Функции выбирают путем построения степенного и показательного уравнений регрессии —"с последующим сравнением сумм квадратов отклонений расчетных значений себестоимости добычи нефти и попутного газа от фактических (табл. 18). Из табл. 18 видно, что наименьшую остаточную дисперсию по НГДУ Укрнефти имеет кинетическая производственная функция. [c.69]
В настоящее время ряд наших экономистов — А. Я. Боярский, И. Г. Венецкий, Г. С. Кильдишев, П. П. Маслов, Л. П. Чернышев, Н. С. Четвериков, В. В. Швырков и др. поддерживают построение уравнения регрессии по отклонениям от уровней динамических рядов. Такую же точку зрения выдвигал Б. С. Ястремский. [c.73]
Таким образом, коррелируя уровень динамического ряда методами отклонений от а) уровня динамического ряда и б) уровня динамического ряда, включая фактор времени, можно прийти к следующему выводу в условиях линейных и нелинейных тенденций динамических рядов уравнения регрессии, построенных методами коррелирования отклонений от уровня динамического ряда и уровня динамического ряда, включая фактор времени (t), будут тождественны. [c.78]
Сопоставимыми переменные в уравнении регрессии будут в том случае, если их выразить в долях среднеквадратического отклонения (а), т.е. рассчитать стандартизированные бетта-коэф-фициенты (р/) [c.77]
В данном примере для прогнозной оценки объемов продаж по сезонам 2000 г. использован метод сложения. Тренд выделен с помощью трехточечных скользящих средних, а значения 2000 г. рассчитаны уравнением регрессии. Прогнозируемые объемы продаж в каждом из периодов 2000 г. исчислены как сумма оценочных показателей тренда и средних значений сезонных колебаний в каждом сезоне (табл. 4.5). Например, среднее отклонение (колебание) за май — август 1997—1999 гг. определяется так (9,33 + + 11,67 + 12,33 3= 11,И) и т.д. [c.80]
Коэффициент с в формуле (88) — экспериментальный коэффициент, функция диаметра диафрагмы и диаметра ДИКТа. Берется он из таблицы. Смысл коэффициента с можно уяснить из выражения для расхода газа через сужающее устройство, полученного из уравнения (88), для критического истечения газа с учетом отклонений свойств реальных газов от идеальных по методике [12] [c.203]
Коэффициенты регрессии в уравнении связи имеют разные единицы измерения, что делает их несопоставимыми, если возникает вопрос о сравнительной силе воздействия факторов на результативный показатель. Чтобы привести их в сопоставимый вид, все переменные уравнения регрессии выражают в долях среднеквадратического отклонения, другими словами, рассчитывают стандартизированные коэффициенты регрессии. Их еще называют бетта-коэффициентами по символу, который принят для их обозначения (р). [c.150]
