При построении кривой распределения вероятностей получения прибыли приняты последующие предположения. [c.177]
Исходя из кривой вероятностей получения прибыли построим кривую распределения вероятностей возможных потерь прибыли, которую, собственно, и следует называть кривой риска. Фактически это та же кривая, но перестроенная в другой системе координат (см. рис. 9.6). [c.178]
Выделим на изображенной кривой распределения вероятностей потерь прибыли (дохода) ряд характерных точек. [c.178]
| Рис. 9.6. Типичная кривая распределения вероятностей возникновения определенного уровня потерь прибыли | 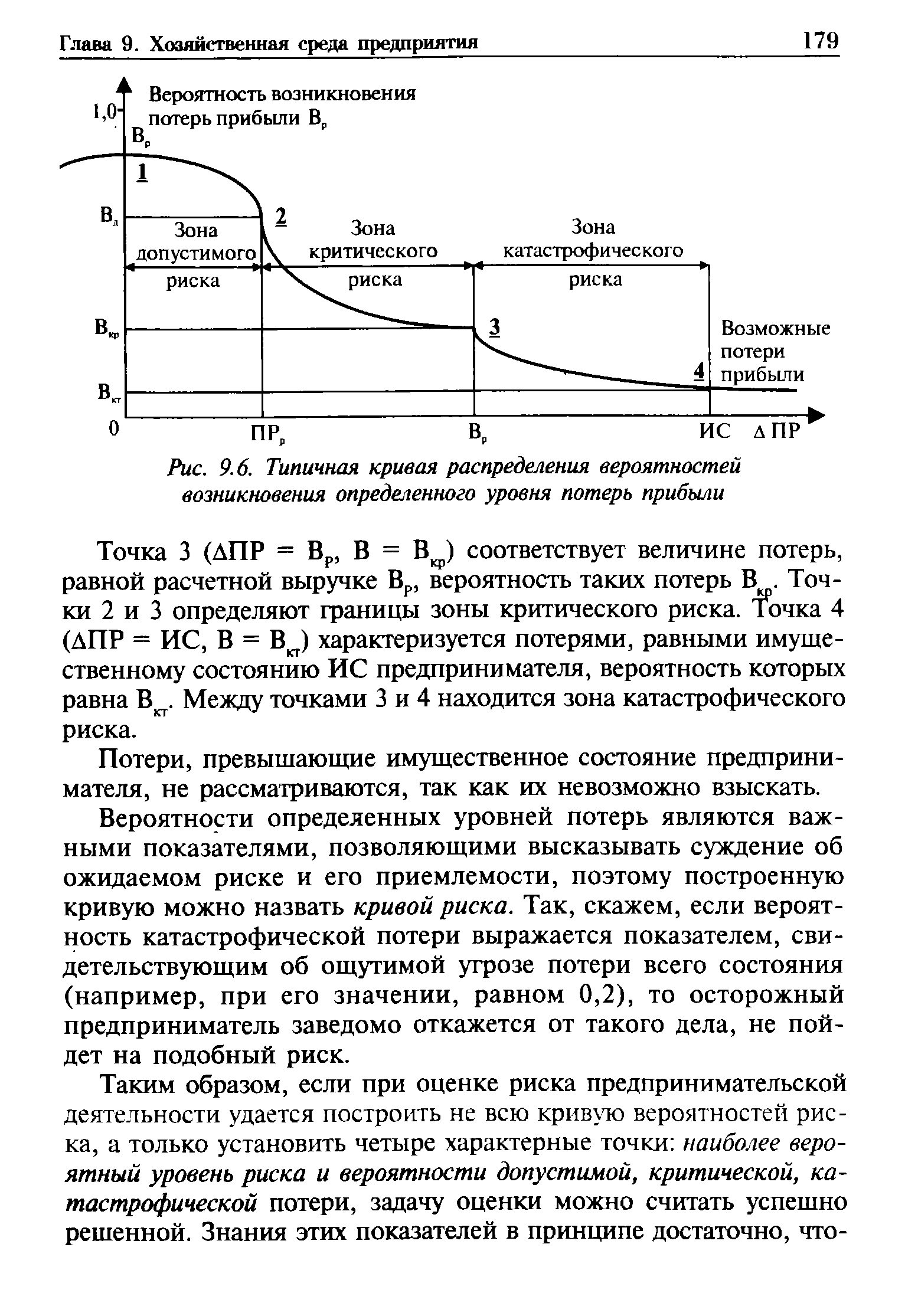 |
Можно даже ограничиться получением экспертных оценок вероятностей возникновения определенного уровня потерь в четырех характерных точках, т.е. установить экспертным образом показатели наиболее вероятных, допустимых, критических и катастрофических потерь, имея в виду как их уровни, так и вероятности. По этим четырем характерным точкам несложно воспроизвести ориентировочно всю кривую распределения вероятностей потерь. Конечно, при небольшом массиве экспертных оценок график частот недостаточно представителен, а кривую вероятностей, исходя из такого графика, можно построить лишь сугубо приблизительно. Но все же определенное представление о риске и характеризующих его показателях можно получить, а это уже значительно лучше, [c.182]
Изменение надежности плана обусловлено как изменением его эластичности, так и выходом в различные диапазоны кривых распределений вероятности обнаружения тех или иных запасов. Наконец, потенциальная адаптивность плана меняется вследствие изменения как трех рассмотренных его адаптивных характеристик, так и динамики затрат при варьировании кратностью запасов. [c.54]
Оценка количественного влияния кратности запасов на адаптивные характеристики плана и общая постановка этой задачи возможны, например, в рамках многоцелевой оптимизации. Запасы газа различных категорий могут быть охарактеризованы кривыми распределения вероятностей с разными параметрами этих зависимостей. Отсюда возможна постановка задачи обоснования кратности запасов в условиях, когда одновременно определяется и оптимальная структура запасов по их категориям. [c.54]
Кривые распределения вероятностей для прогнозных запасов могут рассматриваться при этом как некоторые априорные зависимости, а те же кривые для промышленных запасов — как апостериорные. [c.55]
В настоящем разделе идея риска рассмотрена под углом зрения его изменчивости, а также охарактеризованы понятия кривых распределения вероятностей. Лица, считающие риск качественным явлением, не поддающимся точному прогнозированию, возможно, не подозревают о наличии возможности количественного выражения риска. [c.400]
Распределение вероятностей — это перечень различных возможных событий с указанием вероятности наступления каждого из них. Его можно представить графически в виде кривой распределения вероятностей. Кроме того, ожидаемый доход от инвестиции — это взвешенный средний доход его рассчитывают как сумму всех потенциальных доходов, взвешенных по вероятности возникновения каждого из них. Если все события равновероятны, взвешенный средний доход эквивалентен средней арифметической. Следовательно, ожидаемый доход, средняя, арифметическая средняя — все это синонимы. К сожалению, названные термины полностью не описывают распределение вероятностей. Как это ни странно, сказанное относится и к случаю, когда средняя из различных множеств наблюдений, относящихся к двум переменным, идентична. [c.402]
Кривые распределения вероятностей [c.405]
Охарактеризованный выше вывод заставляет кредитного аналитика рассмотреть некоторые другие статистические понятия. Многим должностным лицам становится не по себе при мысли о необходимости рассмотреть кривую распределения вероятностей, однако представляется совершенно необходимым учесть следующие два момента. [c.405]
Кредитных аналитиков часто интересует один край кривой распределений вероятностей вероятность неудачи. Разумеется, такого повышения степени доверия можно добиться при определенном количестве стандартных отклонений от средней. [c.407]
Графики (а) и (б) на рисунке 20-9 поясняют вышесказанное. На них сравниваются доходы при исполнении двух опционов с одинаковыми ценами исполнения и с одинаковой ценой акции. Графики основаны на допущении, что цена акции равна цене исполнения (как в точке Сна рисунке 20-8), хотя это не обязательное допущение. Единственное отличие состоит в том, что предсказать цену акции Y на дату исполнения опциона по ней (рисунок 20-96) гораздо труднее, чем цену акции X на дату исполнения опциона по ней. Вы можете это видеть при наложении на рисунки кривых распределения вероятностей. [c.542]
Неопределенная информация вводится в модель в виде кривой распределения вероятностей. [c.432]
Более полное представление о риске дает кривая распределения вероятностей потерь. Это графическое изображение зависимости вероятных потерь от их уровня показывает насколько вероятно возникновение тех или иных потерь (рис. 2). [c.44]
Как выглядит кривая распределения вероятности потерь [c.60]
Прямоугольники рис. 3.4 характеризуют нечеткие множества, а кривая - распределение вероятности. Они описывают одну и ту же зависимость. Но и без использования понятия нечеткого графика интуитивно ясно, что эти две функции семантически достаточно близки. Может быть также показана связь функции принадлежности множеству с другими аналитическими функциями. И основание для выбора формы представления во всех случаях кажется очевидным если известно аналитическое представление функции - надо использовать его, если нет - может быть использована функция принадлежности множеству. [c.97]
Если нанести на кривую распределения вероятностей получения потерь Р(П) граничные точки рисков D, К, Kt, то представляется возможным установить вероятность возникновения соответствующих рисков. В среднем для зоны I (допустимых рисков) вероятность возникновения такой ситуации возможна в 70 случаях из 100 (условный пример), для зоны II критические риски могут возникнуть в 40 случаях из 100 и для III зоны (зоны катастрофических рисков) в 20 случаях из 100. Из этого видно, что любой проект имеет определенную степень рисков. [c.605]
| Рис. 16.7. Кривая ( -распределения вероятностей времени выполнения | 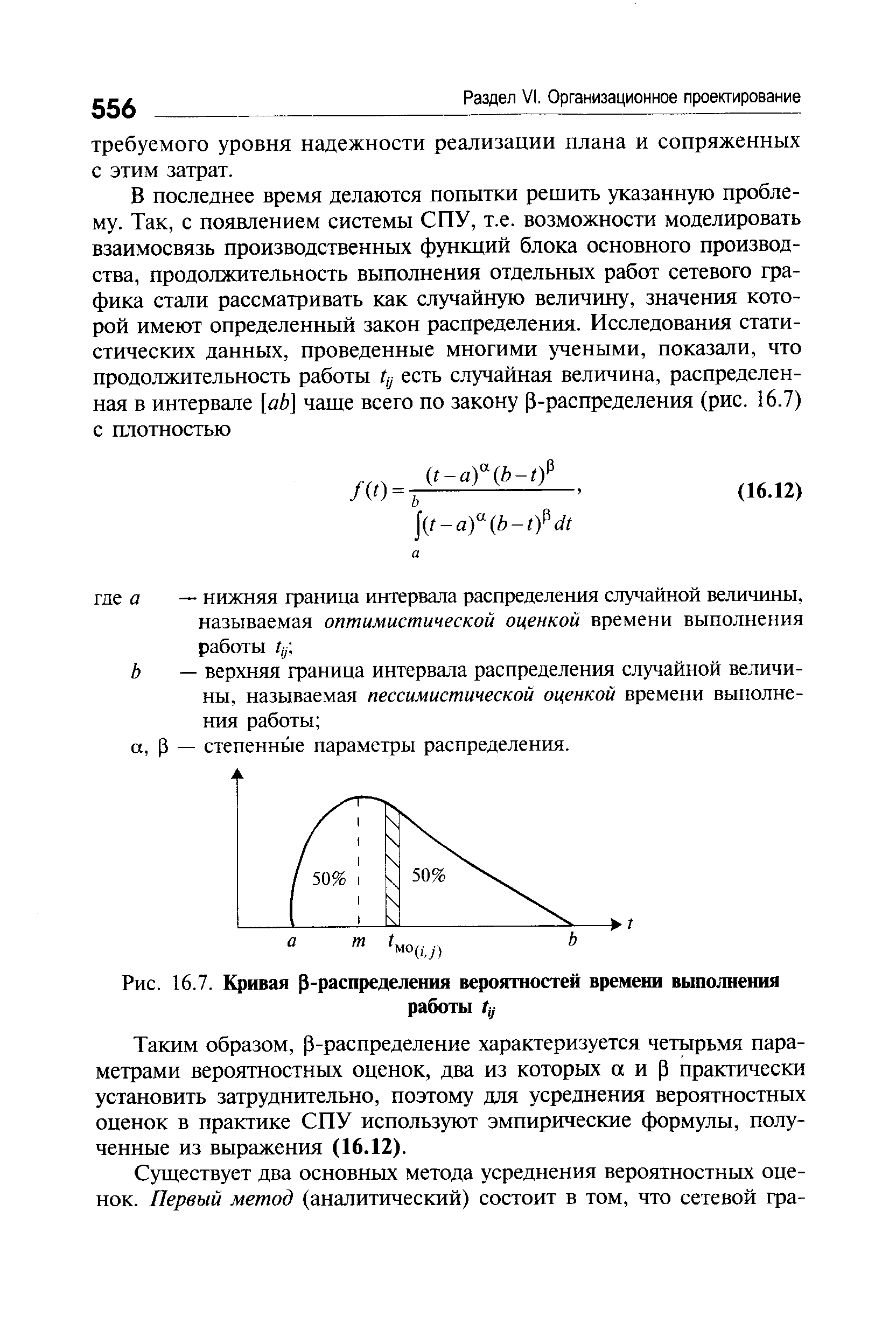 |
Наиболее желательно, чтобы эксперты дали свои оценки вероятностей возникновения определенных уровней потерь, по которым затем можно было бы найти среднее значение экспертных оценок и с их помощью построить график кривой распределения вероятностей. [c.17]
Нормальное распределение является одним из наиболее важных видов распределения вероятностей, используемых при принятии управленческих решений. Этот вид распределения можно обнаружить во многих практических примерах, и он особенно ценен при рассмотрении выборок из большой совокупности. Нормальное распределение, представленное на рис. 2.11, — симметричное, колоколообразное и может быть полностью определено значениями средней арифметической и среднеквадратического отклонения. Средняя арифметическая (ц) определяет центр распределения, а среднеквадратическое отклонение (ст) определяет его разброс. На рис. 2.12 показано, как разница в значениях средней арифметической влияет на положение графика, а на рис. 2.13 показано, как увеличение значения среднеквадратического отклонения меняет размах кривой. Однако, несмотря на изменение значений арифметической средней и среднеквадратического отклонения, базовая форма нормального распределения, определенная нормальной кривой, сохраняется. [c.78]
В этой главе мы также рассмотрели распределение вероятностей. В частности, нормальное распределение, определяемое значениями средней арифметической и среднеквадратического отклонения. Непрерывное распределение вероятностей играет важную роль, оно возникает в ряде реальных ситуаций и особенно полезно при рассмотрении результатов выборочного обследования. Например, независимо от формы распределения, очерчиваемой исходной совокупностью, при взятии больших выборок и определении значений средних эти средние имеют тенденцию, что является фактом, приближаться к нормальному распределению. Знание такого распределения позволяет оценить вероятности различных переменных, например результаты оценочных тестов, критические объемы производства, поступление пациентов и длительность реализации проекта. Далее, нормальное распределение можно использовать при прогнозировании вероятностного диапазона получаемых значений, что достигается путем оценки участков под нормальной кривой. Это лежит в основе некоторых прак- [c.93]
Таблица 14Б.1 показывает пространство нормального распределения, т. е. А стандартных отклонения влево и вправо от среднего. Проверка предусматривается по методу "один хвост", так как мы рассматриваем либо одну, либо другую область распределения. Участок под кривой, соответствующий вероятности того, что имело место 1,5 стандартных отклонений или более вправо от средней, на рис. 14.9 изображен заштрихованной площадью. По табл. 14Б.1 находим, что данному отклонению соответствует [c.407]
График плотности вероятности называется кривой распределения. [c.31]
Геометрически свойства 1 и 4 плотности вероятности означают, что ее график — кривая распределения — лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице. [c.32]
Ру - Д, ру + А). Тогда доверительная вероятность, или надежность оценки, определяемая площадью под кривой распределения на интервале (Ру - Д, Р + Д), как нетрудно видеть из [c.110]
Предположим далее, что известен закон распределения вероятности поставок /-го ресурса. На рис. 6 iSj фиксирует положение потребности оптимального плана в у -м ресурсе на кривой распределения . [c.36]
Из графика видно, что распределение вероятностей проектов А" и Б" имеют одинаковую величину расчетного дохода, однако в проекте А" кривая уже, что свидетельствует о меньшей колеблемости вариантов расчетного дохода относительно средней его величины R, а следовательно и о меньшем уровне риска этого проекта. [c.153]
Случай 1. Минимальное возможное значение распределения вероятности NPV выше, чем нулевое (см. рис. 7.7, а, кривая /). Вероятность отрицательного NPV равна 0, так как нижний конец кумулятивного профиля риска лежит справа от нулевого значения NPV. Так как данный проект имеет положительное значение NPV во всех случаях, ясно, что п р о ект принимается. [c.246]
Случай 2. Максимальное возможное значение распределения вероятности NPV ниже нулевого (см. рис. 7.7, а, кривая 2). Вероятность положительного NPV равна 0, так как кумулятивный профиль риска лежит слева от нулевого значения NPV. Так как данный проект имеет отрицательное значение NPV во всех случаях, ясно, что проект не принимается. [c.248]
Случай 3. Максимальное значение распределения вероятности NPV больше, а минимальное — меньше нулевого (см. рис. 7.7, а, кривая 3). Вероятность нулевого NPV больше 0, но меньше 1, так как вертикаль нулевого NPV пересекает кумулятивный профиль рисков. Так как значение NPV может быть как отрицательным, так и положительным, решение будет зависеть от предрасположенности к риску инвестора. По-видимому, если математическое ожидание NPV меньше или равно 0 (пик профиля рисков слева от вертикали или вертикаль точно проходит по пику), проект должен отклоняться от дальнейшего рассмотрения. [c.248]
Анализ проектов, для которых распределение вероятностей известно, позволяет либо определить кривую доходов, которые можно сравнивать с некоторыми пороговыми значениями, либо характеризовать различные проекты величиной ожидаемого дохода и его стандартного отклонения. В последнем случае предполагается, что существует критерий выбора, зависящий [c.154]
Исходя из стохастической природы исследуемого объекта любую точку на графике рис. 67 можно считать исходом, имеющим некоторую вероятность для заданного объема работ, поэтому аналогом производственной функции геологоразведочных работ является двумерная функция распределения вероятностей возможных исходов. Изолинии этих вероятностей дают представление производственных функций в виде семейства кривых, каждой из которых соответствует вероятность, или показатель надежности, реализации данного направления ГРР. [c.201]
В случаях, когда кривые распределения времени пролеживания деталей и сборочных единиц в переходящих заделах описываются функциями, отличными от показательного закона, необходимо использовать соответствующие им интегральные функции накопленных вероятностей. [c.79]
Расчетно-аншштические методы построения кривой распределения вероятностей потерь и оценки на этой основе показателей предпринимательского риска базируются на теоретических представлениях. К сожалению, прикладная теория риска хорошо разработана только применительно к страховому и игровому рискам. Элементы теории игр в принципе применимы ко всем видам предпринимательского риска, но прикладные математические методы оценочных расчетов производственного, коммерческого, финансового рисков на основе теории игр пока не созданы. [c.182]
Особую группу Э. м. составляют статистические и стохастические (теоретико-вероятностные) модели. Сюда относятся прежде всего модели, основанные на выравнивании статистич. рядов, напр. а) модели корреляционного исчисления (см. Корреляционные исчисления в статистике), устанавливающие тип зависимости одних статистически характеризуемых явлений от других при помощи т. н. уравнений регрессии, рассчитываемых способом наименьших квадратов, а также тесноту связи между этими явлениями при помощи математически рассчитываемого коэффициента корреляции б) модели статистич. распределения, описывающие к.-л. сложное явление (напр., состояние производительности труда или зарплаты) при помощи ряда рассчитанных параметров распределения (средняя величина, среднее квадратическое отклонение и т, д.) и тео-ретич. кривой распределения вероятностей, построенной на основании этих параметров и являющейся, по существу, математич. моделью реального распределения. К Э. м. стохастического характера, получившим в последнее время большое распространение, относятся модели теории массового обслуживания, к-рыми, напр., описываются процессы многостаночного обслуживания. [c.430]
Установление временных оценок основано на предположении, что вероятность срока выполнения работ подчиняется закону нормального распределения и три оценки связаны между собой кривой одновершинного распределения вероятностей. [c.279]
Уравнение (7.7) называют стандартным уравнением нормальной кривой. Величина/ достигает максимума при / = 0, в этом случае е 2/2 = 1. По мере увеличения / величина е 2/2 уменьшается, и соответственно уменьшается f(t). На рис. 7.1 приведен график кривой нормального распределения вероятностей. Ординаты на графике соответствуют вероятностям при том или ином значении /. Чтобы определить вероятность значений в интервале от /, до >2, следует найти отношение части площади кривой, заключенной между орди- [c.167]
Асимметрия служит для оценки симметричности распределения случайной величины относительно средней. Если асимметрия — положительное число, распределение имеет сдвиг в сторону положительных значений, иначе — в сторону отрицательных значений. Эксцесс является характеристикой остроконечности или сглаженности кривой распределения плотности вероятности случайной величины. Эксцесс равен нулю для нормального распределения, положителен для остроконечных и отрицателен для сглаженных по сравнению с нормальной плотностью распределения. [c.462]
Распределение вероятностей удобно характеризовать величиной вероятности неудачи р0. Имея такой параметр, можно построить семейство кривых, отражающих связь заданного распределения и математического ожидания количества, площади структур и количества информации. На рис. 1 приведены при различных значениях р0 графики I(p0ty — количество информации и P(p0k) — площади ожидаемых структур. Графики иллюстрируют основные свойства информации с увеличением частоты наблюдений происходит насыщение информации 4 — уменьшается приращиваемое количество и падает доля положительной информации. При увеличении шага [c.150]
Нормальное распределение вероятностей (normal distribution) — наиболее широко используемое непрерывное распределение вероятностей, обычно имеющее вид колоколобразной кривой и полностью описываемое математическим ожиданием и дисперсией. [c.326]
Смотреть страницы где упоминается термин Кривые распределения вероятностей
: [c.560] [c.17] [c.656] [c.168]Смотреть главы в:
Анализ финансовых отчетов (на основе GAAP) -> Кривые распределения вероятностей
