Индикатор прогноза временных рядов (TSF) показывает статистическую тенденцию цен за определенный период времени. Эта тенденция определяется на основе анализа линейной регрессии. В отличие от прямых линий тренда линейной регрессии (см. стр. 90), график индикатора TSF — это кривая, составленная из последних точек множественных линий тренда линейной регрессии. Поэтому индикатор TSF иногда называют индикатором скользящей линейной регрессии или регрессионным осциллятором . [c.168]
Назначение индикатора видно уже из его названия — он позволяет прогнозировать цены следующего периода. Такая оценка основана на ценовой тенденции бумаги за заданный период (напр., 20 дней). Если текущая тенденция сохраняется, значение индикатора прогноза временных рядов и есть прогноз цены на следующий период. [c.168]
При этом прогноз временного ряда строится по формуле [c.25]
Простейшие методы восстановления зависимостей в детерминированном случае исходят из заданного временного ряда, т.е. функции, определенной в конечном числе точек на оси времени. Задачам анализа и прогноза временных рядов посвящено много литературы. Временной ряд при этом часто рассматривается в рам- [c.136]
Прогнозы временных рядов на основании их собственной динамики (метод тренда) предполагает зависимость некоторых групп доходов и расходов лишь от времени. Он исходит из постоянных темпов изменений (постоянный темп роста) или постоянных абсолютных изменений (линейный временной тренд). Его существенным недостатком является игнорирование экономических и демографических условий. [c.96]
Здесь рассматривается набор линейных параметрических моделей. Речь здесь идет не о моделировании временных рядов, а о моделировании их случайных остатков ,, получающихся после элиминирования (вычитания) из исходного временного ряда xt его неслучайной составляющей (тренда). Следовательно, в отличие от прогноза, основанного на регрессионной модели, игнорирующего значения случайных остатков, в прогнозе временных рядов существенно используется взаимозависимость и прогноз самих случайных остатков. [c.40]
| Рисунок 4.23. Прогноз временного ряда | 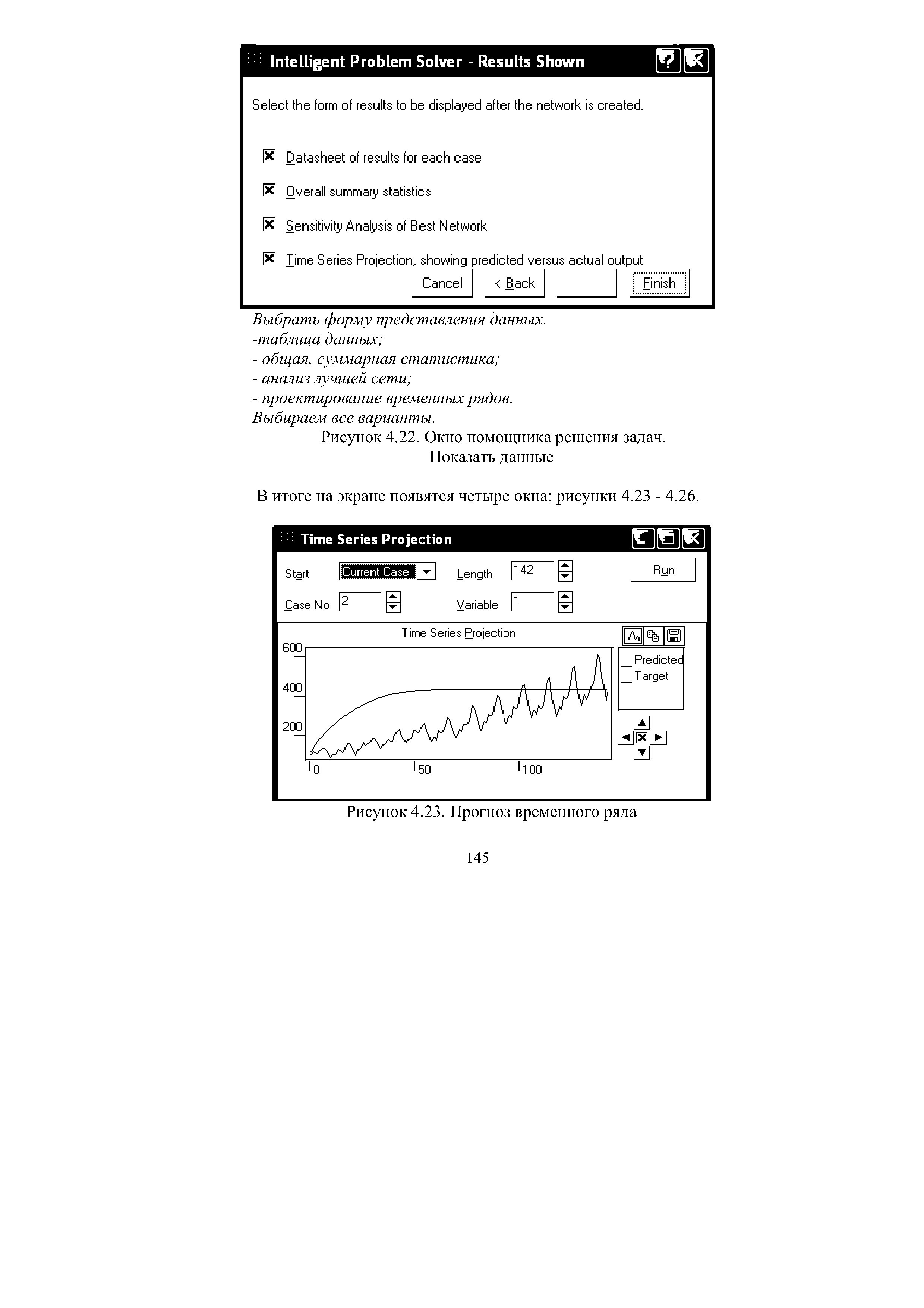 |
Определение тенденции временных рядов. Выявление тенденций изменения экономического явления во времени (или выравнивание динамического ряда) является наиболее простым методом количественного анализа и прогноза динамики явления. Экономическое явление рассматривается здесь как функция от времени. Закономерности изменения изучаемого явления во времени, установленные на базе фактических данных, в данном случае распространяются на прогнозируемый период. Однако метод экстраполяции действующей временной тенденции можно считать оправданным и эффективным только в том случае, если прогнозируемый [c.53]
Однако для обеспечения надежности прогнозирования необходимо исследовать случайную компоненту временного ряда, определить характер (закон) распределения случайных величин. Если случайные величины е f нормально распределены и между собой независимы, тогда определяются интервалы [34, 54], в которые с определенной вероятностью попадают значения полученного нами прогноза. [c.54]
Какую из форм связи следует принять для прогноза, можно окончательно решить только после проведения экономического анализа исходных временных рядов [32, 40]. [c.54]
Существует множество функций, использование которых позволяет отображать реальные тенденции и изменение их во времени с большей или меньшей степенью точности. При выборе определенного типа функции нельзя ориентироваться только на статистические критерии уравнения регрессии, а прежде всего необходимо провести экономический анализ временного ряда, сформулировать определенные предпосылки анализа и прогноза динамики себестоимости добычи нефти. [c.55]
Вычленение и анализ такого элемента временных рядов, как случайные колебания, может использоваться для определения вероятных ошибок и оценки надежности модели прогнозирования. Случайные колебания расцениваются как ошибки прогноза. Разность между фактическими и прогнозируемыми значениями характеризует допущенную ошибку. Для оценки ошибок существуют статистические показатели — средняя ошибка и среднеквадратическая ошибка. Чем меньше значения этих критериев, тем больше надежность прогнозной модели. [c.82]
Обычно для признания модели объективной ее проверяют путем сравнения фактических и прогнозных показателей, прежде чем использовать в дальнейших исследованиях. Эффективным может оказаться прием, когда прогнозная модель формируется исходя из усеченных исторических данных, т.е. фактические значения последнего периода исключаются из прогнозных расчетов и используются как фактические показатели для оценки прогноза. Надежность модели зависит от протяженности временного ряда, как правило, не менее 4—5 лет, причем без нетипичных данных. [c.82]
Как видно из графика на рис. 6.3, имеются существенные колебания показателей объема продаж. Однако отмечается видимая тенденция к увеличению объема продаж, и соответствующий тренд можно выделить с помощью методов регрессии. Линия регрессии показана на графике (рис. 6.3). Из графика видно, что зависимость определена не столь четко, как в предыдущем примере. Так, коэффициент корреляции для этих данных будет значительно меньше по величине, и вообще может оказаться незначимым. Долговременный тренд может быть линейным или нелинейным. Эти данные трудно анализировать из-за сильных расхождений между соседними значениями. Часто, когда мы имеем дело с такого рода данными, необходимо сгладить колебания, и только потом можно сделать какой-либо имеющий смысл прогноз. Методы сглаживания данных временных рядов будут более подробно рассмотрены в последующих разделах. [c.188]
При анализе расхождений результатов применения двух сглаживающих констант при выделении тренда следует обратить внимание на два момента. Во-первых, временной лаг, который очевиден при а=0.1, гораздо менее выражен при а=0.3. В целом, чем больше значение при вычислении сглаженных значений, тем последние более чувствительны к изменениям в последних значениях временного ряда. То есть в этом случае сглаженные значения отстают от значений временного ряда не столь сильно, как это происходит при более малых значениях сглаживающей константы. Этот фактор не играет никакой роли, если отсутствует существенное изменение в общем тренде временного ряда. Однако он крайне важен при составлении прогнозов, когда отмечается значимое восхождение или нисхождение общего тренда временного ряда. Значения, полученные в нашем примере при <х=0.3, лучше отражают общий тренд, чем те, которые рассчитаны при а=0.1, что видно из рис. 6.7. [c.195]
Точность прогноза однозначно зависит от применяемой модели. Однако, вышесказанное не означает, что при составлении того или иного прогноза приемлема только какая-нибудь одна модель. Вполне возможно, что в ряде случаев несколько различных моделей выдадут относительно надежные оценки. В любой модели прогнозирования основным элементом является тренд. В большинстве рассмотренных в этой главе примеров предполагается, что тренд является линейным. Но это может быть и не так, и многие временные ряды, связанные с хозяйственной и финансовой деятельностью, выказывают нелинейный тренд. Другими элементами модели прогнозирования являются сезонные и циклические колебания, а также случайные колебания, которые невозможно предсказать в определенные временные точки. [c.215]
Существуют различные методы прогнозирования, учитывающие характер протекания процессов и значения случайной величины временного ряда. Если вариация средних значений незначительна, для прогноза на короткие интервалы времени применяется метод скользящего среднего. Если поздние значения временного ряда имеют большую значимость для прогноза, а начальные значения — меньшую, применяется метод экспоненциального сглаживания. [c.464]
Метод скользящего среднего предполагает, что все наблюдения временного ряда имеют одинаковую значимость ( вес ) для прогноза. Каждое значение временного ряда, кроме начальных, участвует в формировании нескольких прогнозных значений [c.464]
Метод экспоненциального сглаживания предполагает, что последние значения временного ряда более значимы для прогноза. Каждое значение участвует в формировании прогнозных значений с переменным весом , который убывает по мере устаревания данных [c.466]
В главах (1—10) авторы ограничились рассмотрением в основном линейных эконометрических моделей как наиболее простых и обладающих меньшим риском получения значительных ошибок прогноза. По той же причине изучение временных рядов было ограничено рассмотрением в основном стационарных рядов. [c.4]
В этой главе мы остановимся на некоторых общих понятиях и вопросах, связанных с временными рядами, использованием регрессионных моделей временных рядов для прогнозирования. При анализе точности этих моделей и определении интервальных ошибок прогноза на их основе, будем полагать, что рассматриваемые в главе регрессионные модели временных рядов удовлетворяют условиям классической модели. Модели временных рядов, в которых нарушены эти условия, будут рассмотрены в гл. 7, 8. [c.133]
Прогноз развития изучаемого процесса на основе экстраполяции временных рядов может оказаться эффективным, как правило, в рамках краткосрочного, в крайнем случае, среднесрочного периода прогнозирования. [c.146]
В основе всех прогнозов лежат три информационные базы что говорят люди, что они делают и что они сделали. Первая база — что говорят — формируется по результатам опросов покупателей и тех, кто вступает в контакт с ними, например работников службы сбыта или независимых экспертов. При составлении прогноза на основе что люди делают используется эксперимент по продвижению нового продукта на пробном рынке с целью определения реакции покупателей. Последняя информационная база — что сделали — создается на основе анализа данных о поведении потребителей в последние годы, временных рядов или статистического анализа спроса. [c.198]
Факт, что хаотические модели дают хорошие приближения для финансовых временных рядов, говорит о важности изучения поведения рынков как нелинейных динамических процессов и является дополнительным доводом в пользу применения различных нелинейных методов и в том числе нейронных сетей для создания прогноза. [c.115]
Сначала по первому способу определяются краткосрочные прогнозы. Затем, по мере поступления данных об общем прогнозе на несколько ближайших лет, таким же способом обрабатываются смешанные фактически-расчетные временные ряды. Результаты обработки в виде частных среднесрочных прогнозов поступают на соответствующую верификацию, и процесс повторяется. [c.57]
Блок 3 — прогнозирование потребности по управлению в целом вторым способом. Подробное описание алгоритма расчетов, предусмотренных этим блоком, приводится в разделе Алгоритм решения отдельных блоков . Как и в блоке 2, в блоке 3 первоначально определяется краткосрочный прогноз потребности. После верификации краткосрочного прогноза и корректировки временных рядов, используемых для расчетов показателей, аналогично обрабатываются смешанные фактически-расчетные ряды для получения среднесрочного, а затем и долгосрочного прогнозов. При долгосрочном прогнозировании определяется суммарная потребность в автобензине и дизельном топливе. [c.57]
Брусиловский П.М., Фридлянд A.M. Коллективные решения при формировании прогнозов временных рядов. //Приложение математических моделей к анализу эколого-экономических систем. -Н. Наука. -1988. -С.160-172 [c.180]
Индикатор прогноза временных рядов (см. стр. 138) показывает то же, что и линия тренда линейной регрессии. Любая точка на графике этого индикатора равнозначна конечной величине линии тренда линейной регрессии. Например, значение в конечной точке Юдневной линии тренда линейной регрессии совпадает со значением Юдневного индикатора прогноза временных рядов. [c.110]
Пакет промышленных программ для анализа и прогноза временных рядов/Френкель А. Д., Гарбер Е. В., Шифрин Г. М., Горелик Н. А, — В кн. II Всесоюз. школа-семинар Программно-алгоритмическое обеспечение прикладного многомерного статистического анализа Тез. докл., М., 1983, с. 167—169. [c.464]
В прогнозировании можно идти двумя путями. Первый - попытаться причинно-следственный механизм, т.е. найти факторы, опреде-поведение прогнозируемого показателя, прогноз по которым либо известен, либо его дать несложно. Этот путь приводит к экономико-математическому моделированию, построению модели поведения экономического объекта. В настоящее время данный путь широко используется при прогнозировании природопользования. Второй путь - не вдаваясь в механику движения, попытаться предсказать будущее положение, анали-временной ряд изолированно. В современной практике прогнозиро-природопользования такие методы изолированного анализа и про-почти не применяются, но преимущество этих методов диктует необходимость их более широкого применения. [c.31]
Чем более достоверно предположение о подобии будущего прошлому, тем вероятнее точность прогноза. Таким образом, анализ временных рядов, вероятно будет бесполезен в ситуациях с высоким уровнем подвижности или когда произошло значительное, всем известное изменение. Например, директор ресторана Бюргер Кинг не смог бы предсказать спрос на гамбургеры в ноябре, если бы знал, что фирма Мак Доналдс собралась открыть свой ресторан рядом с его рестораном в последнюю неделю октября. Подобным образом, региональная телефонная компания смогла использовать метод анализа временных радов для прогнозирования спроса на рекламу в телефонном справочнике Иелоу Пейдж в грядущем году, поскольку ее бизнес стабилен, а конкуренции практически нет. Тем не менее фирма Ралф Лорен , вероятно, не смогла бы воспользоваться этим методом для прогнозирования рождественского спроса на новую модель мужских сорочек, поскольку конкуренция в области модной одежды исключительно высока, а вкусы потребителей меняются каждый год. [c.242]
По степени достоверности прогнозы делятся на гипотетические, аналитико-расчетные и планово-расчетные. Гипотетические прогнозы рассматривают общие тенденции развития науки и техники, они в значительной мере основаны на мнениях компетентных специалистов, на экспертных оценках. Аналитико-расчетные прогнозы строятся на базе анализа развития рассматриваемых объектов и процессов с использованием вероятностных расчетных методов (корреляционного анализа, динамических рядов и др.). Планово-расчетные прогнозы в наибольшей степени используются для про-гнозирэвания выполнения планов. Они основаны на том, что планы при их разработке носят вариантный и вероятностный характер. В результате проведения указанных расчетов получают прогноз времени выполнения плана. Планово-расчетные прогнозы имеют наибольшую степень достоверности по сравнению с двумя другими способами прогнозирования, рассмотренными выше. [c.89]
При прогнозировании бюджета возможны различные варианты, иногда оно выполняется экстраполяцией прошлого опыта. В сущности, это прогнозирование от достигнутого результата. Лица, получившие хорошее математическое образование, критикуют так называемый метод трех точек, когда данные за три предыдущих года (месяца, дня) экстраполируются на следующую дату, полагая, что чем больше исходная совокупность, тем точнее будет прогноз. Они пытаются взять данные не за три года (месяца, дня), а за п лет. По этому поводу следует заметить, что, и это очень хорошо обосновано в книге, "прошлое, — как говорит автор, — доминирует над будущим" (гл. 12), и, следовательно, чем больше будет временной ряд, тем больше это прошлое будет доминировать над будущим. Поэтому "три точки" — это наименее плохой вариант для экстраполяции, но сама экстраполяция весьма сомнительна (даже по трем точкам). Дело в том, что подобные расчеты хорошо делать тогда, когда "испытания независимы", т.е. если каждое значение, допустим величина продаж, не зависит от предыдущего. Но на практике, как правило, если в одном периоде продали много, то очень может быть, в следующем не продадут больше (насыщение спроса). [c.935]
ПРОГНОЗИРОВАНИЕ МЕТОДОМ ВЫДЕЛЕНИЯ СОСТАВЛЯЮЩИХ ВРЕМЕННОГО РЯДА. Все большее применение в экономическом прогнозировании (особенно в краткосрочном) находит метод, при котором прогнозируемое значение рассматриваемого показателя в моменты времени fntl, fn+2,. .. определяется как итог прогнозов двух (либо трех) составляющих. Имеем [c.225]
Перспективный анализ прибыли имеет целью выявление наиболее устойчивых закономерностей и тенденций в предшествующем периоде, прогнозирование на их основе показателей на перспективу, выбор альтернатив развития, выработку практических рекомендаций по определению наилучшего варианта развития предприятия. Рассмотрим некоторые практические аспекты использования для перспективного анализа прибыли метода непосредственной экстраполяции корреляционно-регрессионного метода. Метод непосредственной экстраполяции - наиболее простой способ прогноза. Его рекомендуется использовать, если имеется однородная и обширная по объему исходная информация, т. е. достаточно длинный временной ряд. Экстраполяция основана на изучении динамики изменения экономического явления (показателя) в предпрогнозном периоде и перенесения выявленной закономерности на будущее. Достоинство метода состоит в его универсальности, а недостаток - в необходимости проведения большого числа наблюдений, что ведет к снижению достоверности прогноза с увеличением срока его упреждения. [c.126]
Динамический, или временной, ряд представляет собой совокупность числовых данных, характеризующих изменение показателя во времени. При построении временного ряда должна быть обеспечена сопоставимость отдельных его членов. Для этого все элементы должны характеризовать изучаемое явление за равные промежутки времени (для интервальных рядов) или фиксировать его состояние в строго определенные моменты (для моментных рядов). Допускается построение рядов с годовым исчислением признака с использованием более мелких единиц измерения времени квартала, месяца, декады. Это дает возможность исследовать колеблемость показателей не только по годам, но и кварталам, месяцам, декадам. Может возникнуть вопрос, какой длины брать ряд динамики для прогнозирования Единого мнения по этому вопросу нет. Одни авторы считают, что чем длиннее предпрогнозный период (20-30 лет), тем достовернее выводы о перспективах изменения исследуемого явления в будущем. Другие считают, что для прогноза на будущее достаточно двух-трех лет, поскольку длинные ряды динамики преувеличивают роль прошлого в развитии исследуемого объекта. Третьи считают, что наилучшие результаты могут быть получены при использовании рядов динамики, содержащих не менее пяти и не более двадцати членов. [c.126]
Подразделение сбыта и продаж компании АПИ, которое возглавляет Питер Халлиган, в 1997 г. имело оборот свыше 1 млрд. долл. США. Исполнительное руководство подразделения проявляет все большую обеспокоенность в связи с отсутствием глубоких прогнозов по таким направлениям, как возможности увеличения спроса, валютообменный курс доллара США, стоимость затрат на добычу и разведку нефти. Для выработки оценок по ряду показателей исходя из прошлых данных была приглашена консультационная группа Ноекен . С тем чтобы оценить различные переменные, интересующие АПИ, аналитики деловой активности, нанятые Ноекен , помимо качественных методов воспользовались приемами прогнозирования на основе временных рядов. [c.185]
Другие модели строятся с учетом соотношений с другими переменными по методу регрессии, о чем мы говорили в предыдущей главе. Так, например, такая переменная, как покупательский спрос на нефтепродукты, может зависеть от других переменных, в частности, от расходов на рекламу, ценообразования, процентных ставок и валютообменных курсов. Это так называемые причинно-следственные связи, и зачастую они обеспечивают большую точность и надежность прогноза по сравнению с моделями прогнозирования на основе временных рядов. [c.215]
