ТЕОРИЯ ОЖИДАЕМОЙ ПОЛЕЗНОСТИ 7.2.1. Графики функций полезности [c.488]
Постройте график функции полезности, заданной приведенной выше таблицей. Покажите, что рискованный контракт, обещающий долл. с вероятностью р и х.г долл. с вероятностью 1 — р, может быть представлен точкой с координатами [c.78]
Качественно указанные особенности отношения предпочтения ЛПР могут быть отражены графически. На рис. 3.6 представлены графики функций полезности для лиц с различным отношением к стохастическому риску. [c.230]
| Рис. 3.6. Графики функций полезности для лиц с различным отношением к стохастическому риску | 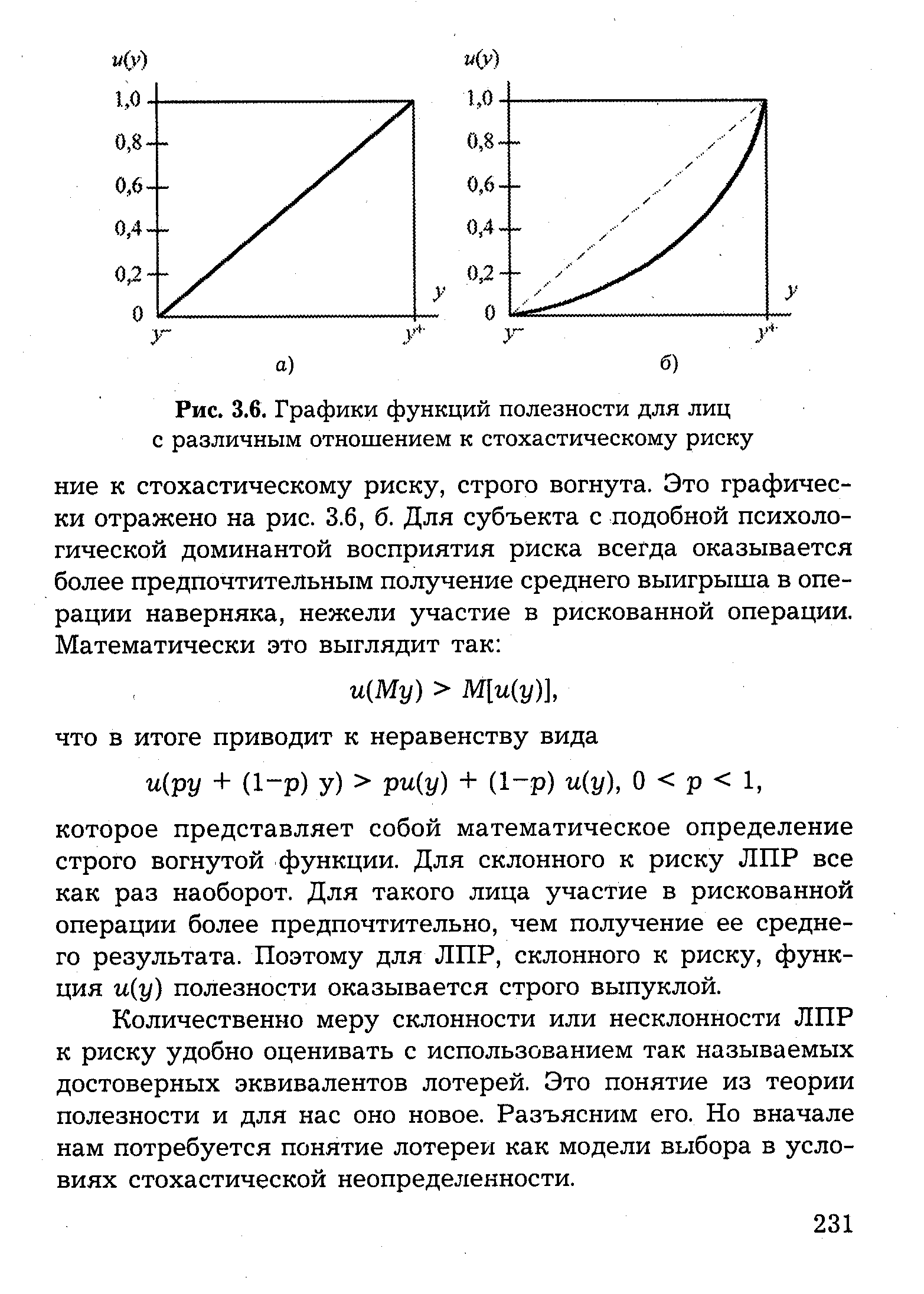 |
Тогда формулу (218) можно рассматривать как функцию полезности инвестора, которая пересекает ось ординат в точке г (см. рис. 77). В данном случае получается веер функций полезности, которые проходят через одну точку г. Более высоко расположенная функция приносит инвестору большую полезность. Оптимальный портфель будет располагаться в точке касания графика функции полезности эффективной границы AB . [c.328]
| Рис. 77. Веер функций полезности инвестора. Оптимальный портфель располагается в точке касания графика функции полезности эффективной границы ЛВС |  |
Определение строгого доминирования можно наглядно проиллюстрировать в случае двух игроков, множества стратегий одного из которых — действительная прямая (см. Рис 149). На рисунке стратегия xl первого игрока строго доминирует стратегию уг. Это выражается в том, что график функции полезности этого игрока по стратегии х2 второго, соответствующий ж1 лежит ниже графика, соответствующего уг. [c.631]
Слабое доминирование можно проиллюстрировать на графике, аналогичном тому, который мы использовали для иллюстрации строгого доминирования. Стратегия xl первого игрока слабо, но не строго доминирует его стратегию у1 (см. Рис. 150), поскольку график функции полезности для х1 не везде строго выше, чем для у . [c.632]
С помощью функций полезности денег можно выразить характерное отношение к ним индивида. Например, пусть график функции полезности индивида А - это кривая а на рис. 7.8, а индивида Б - кривая б на том же рисунке. [c.58]
Для интерпретации результатов целесообразно построить графики функций полезности. По значениям функций полезности для каждой характеристики, приведенной в табл. 21.6, i - строены графики функций полезности, показанные рис. [c.800]
Имея в виду, что мы используем порядковые свойства функции полезности, мы можем теперь рассмотреть конкретную функцию. Функция U (F, С) = F говорит нам, что уровень удовлетворения потребностей, связанный с потреблением F единиц первого товара и С единиц второго товара, является произведением F . На рис. 3.16 показаны некоторые кривые безразличия, соответствующие данной функции. Чтобы начертить график, сначала выбираем конкретный набор, скажем F = 5 и С = 5, и определяем соответствующий уровень полезности 25. Затем строим кривую безразличия как совокупность всех наборов потребительских товаров и услуг, для которых F = 25 (например F=10, С =2,5 F=2,5, С =10). Вторая кривая безразличия содержит все наборы, для которых F = = 50, а третья — F = 100. [c.93]
Показанный в предыдущем параграфе график функции предельной полезности (рис. 1.1, б) представляет собой линию с отрицательным наклоном, построенную в координатах MU, Q. Подобным же образом изображается обычно и линия индивидуального спроса, основное назначение которой состоит в том, чтобы выражать зависимость объема спроса конкретного индивидуума на определенное благо (QD) от уровня его цены (Р). [c.18]
Далее, расположив расчетную полезность по оси у, а цену уверенности по оси х, вычертите соответствующий график. В результате ваша функция полезности будет выглядеть так, как это показано на рис. 2.5. [c.123]
На участке между g in и g ax график функции нечеткой полезности является прямой [c.51]
Линия данного уровня lq функции полезности U =f(Xi, называется кривой безразличия. По определению кривая безразличия есть геометрическое место (или попросту совокупность) всех точек на графике потребительского множества, показывающее все возможные комбинации товаров, обеспечивающие потре- [c.118]
В этом случае существуют две трансакционные линии. Трансакционная линия, которая касается графика функции инвестиций в точке Я, имеет значение лишь для некоторых лиц, принимающих решение, а именно для тех, кто помещает деньги на рынке капитала. Наоборот, трансакционная линия, которая касается функции инвестиций в точке S, является значимой для тех участников рынка, которые хотят получить кредит. Тезисы, которые являются верными для всех лиц, принимающих решения, касаются лишь точек Я и S. Расширения объема реальных инвестиций за пределы точки Я не должно произойти, так как достигаемые благодаря этому доходности меньше ставок процента по вкладам. С другой стороны, сокращение объема реальных инвестиций ниже точки S неразумно, так как эти инвестиции даже при дисконтировании на основе ставки процента по заимствованиям характеризуются положительной чистой сегодняшней стоимостью. Как можно видеть из рис. 1.14, нельзя достичь единогласия в связи с программой реальных инвестиций тогда, когда лица, предлагающие капитал, имеют разные временные предпочтения. Скупердяй будет выступать за программу Я. Нормальный инвестор достигает своего максимума полезности, если выбирает программу N. Расточитель будет выступать за программу 5. Таким образом, теорема разделения Фишера нарушается. [c.31]
Информация о функции полезности может понадобиться на двух этапах — для определения ее градиента и для выбора величины шага при одномерной оптимизации. В большинстве методов градиент (или вектор, параллельный ему) вычисляется с помощью предельных норм замены одного из критериев всеми остальными. Для выбора величины шага ЛПР предоставляется график изменения всех критериев вдоль выбранного направления, и ЛПР должен указать в нем оптимальную , на его взгляд, точку. [c.73]
На рис. 1 представлен график вогнутой функции полезности (для иллюстрации взята функция u(w) = -Jw ). Допустим, что индивид может выбрать вариант поведения, в результате которого его богатство с равными вероятностями примет значение 1 или 49 ед. математическое ожидание богатства [c.649]
Функция полезности, имеющаяся у руководителя в нашем примере, будучи нанесена на график, возрастает с постепенно уменьшающейся скоростью.. Можно сказать, что она показывает уменьшающуюся предельную полезность денег иными словами, ценность каждого дополнительного доллара уменьшается по мере того, как растет вся сумма. Этот человек, как мы видели, оценил предложенные ему рискованные возможности ниже их ожидаемой денежной ценности. Хотя способ действий at имел ожидаемый доход 25000 долл., он не захотел платить 25 000 долл. за возможность участвовать в нем. Он оказался консервативным, или не склонным к риску. Мы можем предсказать, что такой человек будет приобретать различные виды страховых гарантий против крупного риска и будет вести политику диверсификации (рассредоточения капитала по разным вложениям), чтобы уменьшить риск или непостоянство своих доходов. [c.76]
Изобразите на графике вашу функцию полезности в области денежных значений, которые встречались вам на практике при принятии решений. [c.77]
На рис. 3.1 показана эта ситуация для случая двух продуктов. Контур 0—Ь—В—А — Q—0 ограничивает производственное множество g(x) В х 0. На этом же графике показаны изо-кванты функции полезности И(Г) < U(B) < U(B) < /. Нетрудно видеть, что максимум полезности достигается в точке В вектор цен, который ориентирует и потребителя и производителя на эту точку и обеспечивает равновесие спроса и предложения, ор- [c.53]
Вслед за субъективными оценками полезности блага и появлением его ценности для субъекта формируется индивидуальный потребительский спрос на данное благо на соответствующем рынке. При этом динамика положительных субъективных оценок полезности блага, т. е. динамика его ценности, лежит в основе потребительского спроса. Другими словами, закон убывающей предельной полезности причинно обусловливает функцию спроса. Динамика предельной полезности и динамика потребительского спроса соотносятся как сущность и явления, причина и следствие. Внешне это соотношение проявляется в тождественности графиков предельной полезности и спроса (рис. 10.3). [c.212]
По оси абсцисс на графиках отложены величины результатов, а по оси ординат — значения функции и(у) полезности. Психологической доминанте "объективное ЛПР" соответствует функция и(у) = а + Ру. Она представлена на рис. 3.6, а. Параметры а и (3 функции выбраны так, что наименее предпочтительному значению результата у = у соответствует нулевое значение функции полезности, а наиболее предпочтительному результату у = у+ — значение, равное единице. Очевидно, что если пользоваться такой функцией полезности, то это приводит к установлению предпочтений на множестве стратегий по "объективным" показателям типа (3.3), т. е. [c.230]
В теории потребительского спроса на два блага х и у (к примеру, исследуемое х и все остальные у) предпочтения потребителя описываются кривой безразличия U(x,y) = Uk, а бюджетное ограничение (расходы потребителя <, его дохода) в случае, когда потребитель тратит весь свой доход на рассматриваемые блага хрх + уру = I, где /-доход потребителя, а рд и р - цены благ х и у соответственно. Для того, чтобы построить графики этих неявно заданных функций ХА ) в системе координат, где по оси абсцисс отложена величина блага х, а по оси ординат - у, нужно выразить в явном виде величину у как функцию х для обеих зависимостей. Сделаем это для простейшей функции полезности U(x,y)—xy. Для уровня полезности (благосостояния) U0 и дохода / получаем следующие функции [c.38]
При исследовании поведения функции и формы ее графика полезно установить, на каких интервалах график функции обращен выпуклостью вверх, а на каких - выпуклостью вниз. Прежде всего выясним понятие выпуклости графика функции, имеющей на некотором интервале непрерывную производную. [c.65]
Предположим, что в экономике производятся только два потребительских блага — частное (Р) и общественное (G). Имеются два потребителя (А и В) со своими функциями полезности, которым соответствуют кривые безразличия UA и UB. Функция трансформации представлена на графике кривой производственных возможностей Z 2 (рис. 4). [c.245]
Функция полезности U (x удовлетворяющая условиям ( ), ( ), называется выпуклой. Выпуклая функция полезности описывает предпочтения склонного к риску инвестора, а также ситуации, в которых возврат, например прибыль, растет сверхлинейно по отношению к вложениям ж в проекты. Характерной чертой выпуклых функций является то, что отрезок, соединяющий две точки графика функции полезности, находится над графиком. Здесь случайная величина х с математическим ожиданием М(х) предпочтительнее для лица (7, чем детерминированная величина М(х). Разность [c.46]
Карта изоквант представляет собой набор изоквант, каждая из которых показывает максимальный выпуск продукции, достигаемый при использовании определенных сочетаний факторов. Карта изоквант является альтернативным методом описания производственной функции, точно так же как карта кривых безразличия представляет собой один из способов описания функции полезности. Бесконечное число изоквант составляет изоквантную карту. Каждая изокванта ассоциируется с различным объемом выпуска продукции, и эти объемы возрастают по мере движения вверх и вправо по графику. [c.162]
Совок ипь лвтономные расходы и смещение графика совокупных расходов Что является причиной смещения графика совокупных расходов Чтобы ответить на этот вопрос, полезно рассмотреть уравнение, которым задан график совокупных расходов. Предположим, что величина автономных инвестиций равна /0. К тому же нужно помнить, что поскольку упрощенная модель экономики предполагает отсутствие государственного сектора (yd = у), то располагаемый доход равен доходу без налоговых вычетов. Поскольку график совокупных расходов строится путем сложения графиков функции потребления и автономных инвестиций, то уровень совокупных расходов будет равен [c.510]
Критерием, обеспечивающим сужение поля выбора портфеля инвесторов, являются кривые безразличия" [indifferen e urves]. В основе их построения лежат функции полезности инвестора, отражающие его отношение к риску и доходности портфеля. Принципиальный график формирования кривых безразличия инвестора, нейтрального к риску, представлен на рис. 11.4. [c.352]
Решение о количестве, в котором следует потреблять данное благо, — это результат сопоставления потребителем выгод и издержек. Выражая полезность блага в денежных единицах, мы получаем ценность данного блага. В отличие от полезности ценности различных благ для различных потребителей количественно сопоставимы, поскольку выражены в одних и тех же — денежных — единицах. На рис. 5.3 площадь под графиком функции предельной полезности АБ (при выражении полезности в денежных единицах это график предельной ценности или обратной функции спроса) как раз будет равна общей ценности (суммарной выгоде от потребления) данного количества блага (на рисунке это площадь АБГО). [c.117]
Рассмотрим проблему выбора наилучшего потребительского набора, сведя количество благ к двум. Такой шаг не является очень сильным упрощением действительности выбор потребителя можно представить как выбор между потреблением данного блага и всех остальных благ. График Г функции полезности двух переменных, как правило, напоминает своим видом "горку", которая становится все более пологой (снижение предельной полезности). Поскольку работать с трехмерным графиком неудобно, обычно строят его проекции на соответствующие плоскости координат. Так получаются не только уже рассмотренные выше кривые од-нофакторных функций полезности (показывающие зависимость уровня полезности от изменения количества только одного вида благ при неизменных количествах всех остальных видов благ в данном наборе), но и линии данного уровня полезности при различных комбинациях благ в наборе (рис. 5.4). [c.118]
График NPV строится как функция цены капитала. Пересечение кривой NPV с осью абсцисс показывает внутреннюю доходность — JRR. Графики NPV полезны при анализе проектов. С ростом цены капитала NPV убывает. На рис. 8.2 приведены графики NPV проектов А и В. Проект В имеет более высокое значение NPV при низких значениях а й 7,2%, при больших значениях цены капитала больший NPV имеет проект А. Таким образом, NPVB более чувствителен к изменению дисконтной ставки, чем NPVA. Это обусловлено тем, что, напомним, проект А является краткосрочным, а проект В — долгосрочным. [c.195]
Проще всего определить выпуклую функцию геометрически. Для этого полезно ввести понятие надграфика функции. Надграфиком функции называется множество точек, расположенных над графиком функции и на самом графике. Более строго, надграфик функции f(x) — это множество таких точек, координата х которых лежит в области определения функции, а координата у удовлетворяет неравенству у > f(x). [c.572]
Левая часть рисунка иллюстрирует построение графика функции спроса по цене при порядковом измерении полезности (см. лекция 15, раздел 2) гиффенова блага . При фиксированном номинальном бюджете М по мере роста цены блага X наклон бюджетной линии увеличивается. Специфическое расположение кривых безразличия, отражающее изменение предпочтений потребителя при изменении его реального дохода, приводит к тому, что в оптимальном (равновесном) ассортименте увеличивается объем блага с растущей ценой. В результате линия спроса на это благо приобретает положительный наклон. [c.123]
Чаянов построил модель основного равновесия в трудовом хозяйстве. Пусть %— сумма годового дохода крестьянской семьи, тогда первая монотонно возрастающая непрерывная функция/(%) показывает степень тягостности приобретения предельного рубля, а вторая монотонно убывающая непрерывная функция ос(х) показывает исличину предельной полезности этих рублей. По мере возрастания годовой выработки субъективная оценка предельного рубля будет Падать, а тягостность его добычи — всегда возрастать. Из этого следует, что графики функций пересекаются в единственной точке %р для которой выполняется соотношение а(х,) =/(%,) [c.445]
Предположим, что функции полезности Робинзона и Пятницы описаны в задаче 1. Но допустим теперь, что первоначально у Крузо 6 апельсинов, а у Пятницы 2. Допустим, что за каждые 2 апельсина, забираемые у Крузо, Пятница получает только 1, один же апельсин теряется в процессе передачи. Каким будет график потребительских возможностей Какие из допустимых распределений максимизируют общественное благосостояние при утилитаристской функции общественного благосостояния Что происходит при ролсианской функции [c.118]
Смотреть страницы где упоминается термин Графики функций полезности
: [c.8] [c.86] [c.159] [c.314] [c.240]Смотреть главы в:
Теория риска и моделирование рисковых ситуаций -> Графики функций полезности
