Все эти эффекты затрудняют и без того сложную задачу интерпретации коэффициентов регрессии или вообще делают невозможным ее решение без привлечения новых способов обработки и дополнительной информации. В этих условиях нельзя применять уравнение регрессии и для прогноза значений переменной у. В то же время если уравнение регрессии предполагается использовать для целей прогноза значений переменной у только в точках, близких к значениям объясняющих переменных х(1 . .., х из матрицы данных X, то оно может оказаться вполне удовлетворительным независимо от степени связи между предсказывающими переменными качество уравнения регрессии определяется значением коэффициента множественной корреляции Ry.x между переменной у и переменными X (хотя при этом может быть необходимо принять некоторые предосторожности чисто вычислительного характера). Таким образом, последствия мультиколлинеарности тем серьезнее, чем больше информации мы хотим получить из имеющейся совокупности наблюдений. [c.254]
Более правильной на первый взгляд кажется интерпретация коэффициента регрессии а как обусловленная фактором Xi часть интенсивности совместного влияния всех факторов. Коэффициент регрессии а, показывает, на сколько единиц изменяется результативный показатель У в случае изменения факторного показателя Xi на единицу при изменении других факторных показателей аналогично их изменению в условиях исследуемого эксперимента (в рамках исследуемой статистической совокупности наблюдений). Данная интерпретация как будто вообще устраняет проблему применяемости модели — каждая модель по данному формальному подходу имеет содержательную интерпретацию и, следовательно, ее можно применять в процессе принятия решений в качестве истинного отображения реальных связей. Подобное мнение опровергается практикой статистического моделирования. Формальная интерпретация интенсивности влияния отдельных факторов часто противоречит здравому смыслу и практическому опыту субъекта управления. Это означает, что интерпретация коэффициентов регрессии не отражает их сущности. [c.122]
Интерпретация коэффициентов регрессии [c.62]
Интерпретация моделей регрессии осуществляется методами той отрасли знаний, к которой относятся исследуемые явления. Но всякая интерпретация начинается со статистической оценки уравнения регрессии в целом и оценки значимости входящих в модель факторных признаков, т.е. с выяснения, как они влияют на величину результативного признака. Чем больше величина коэффициента регрессии, тем значительнее влияние данного признака на моделируемый. Особое значение при этом имеет знак перед коэффициентом регрессии, который говорит о характере влияния на результативный признак. Если факторный признак имеет знак плюс, то с увеличением данного фактора результативный признак возрастает если факторный признак имеет знак минус, то с его увеличением результативный признак уменьшается. [c.121]
Линейный коэффициент корреляции изменяется в пределах от -1 до +1. Знаки коэффициентов регрессии и корреляции совпадают. При этом интерпретацию значений коэффициента корреляции можно представить следующим образом. [c.123]
Следует отметить, что в принципе качественное различие можно формализовать с помощью любой переменной, принимающей два разных значения, не обязательно О или 1 . Однако в эконометрической практике почти всегда используются фиктивные переменные типа 0—1 , так как при этом интерпретация полученных результатов выглядит наиболее просто. Так, если бы в модели (5.2) в качестве фиктивной выбрали переменную Zj, принимающую значения z,i=4 (для работников-мужчин) и 2/2=1 (для женщин), то коэффициент регрессии оц при этой переменной равнялся бы 1/(4— 1), т. е. одной трети среднего изменения заработной платы у мужчин. [c.117]
Если рассматриваемый качественный признак имеет несколько (k) уровней (градаций), то в принципе можно было ввести в регрессионную модель дискретную переменную, принимающую такое же количество значений (например, при исследовании зависимости заработной платы Y от уровня образования Z можно рассматривать Л=3 значения z,-i=l при наличии начального образования, гд=2 — среднего и г,з=3 при наличии высшего образования). Однако обычно так не поступают из-за трудности содержательной интерпретации соответствующих коэффициентов регрессии, а вводят (k—l) бинарных переменных. [c.117]
Дайте интерпретацию коэффициента эластичности данной модели регрессии. [c.36]
Выберите наилучшее уравнение регрессии. Дайте интерпретацию их параметров и доверительных интервалов для коэффициентов регрессии. [c.84]
Выберите наилучшее уравнение регрессии. Дайте интерпретацию его параметров и доверительных интервалов для коэффициентов регрессии на примере одного из факторных признаков. [c.85]
Поскольку коэффициент регрессии в эконометрических исследованиях имеет четкую экономическую интерпретацию, то доверительные границы интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, —10 < ft < 40. Такого рода запись указывает, что истинное значе- [c.54]
Коэффициент регрессии бета измеряет влияние общей ситуации на рынке в целом на судьбу конкретной бумаги. Если Р>0, то эффективность данной ценной бумаги повышаться при росте эффективности рынка. При Р<0 эффективность данной ценной бумаги будет снижаться при возрастании эффективности рынка. Понять значимость фактора бета поможет его экономическая интерпретация. Если портфель имеет Р = +1, это означает, что доходность бумаги в среднем будет расти на 10%, если доходность рыночного портфеля акций в целом возросла, например, на 10%. Портфель, имеющий Р = 2, вдвое более изменчив, чем общий рыночный портфель. Когда рыночная доходность увеличивается на 10%, доходность такого портфеля увеличивается на 20%. [c.228]
Интерпретация параметров интенсивности влияния факторов fli в многомерных регрессионных моделях определяется наличием и теснотой внутренних связей системы факторных показателей. Хотя наиболее распространенный метод оценки коэффициентов регрессии — метод наименьших квадратов — предполагает статистическую независимость факторных показателей, в практических попытках моделирования хозяйственной деятельности данное требование трудно выполнять и поэтому в общем случае им пренебрегают. Изучаются лишь пути устранения явных искажений, когда направление влияния фактора в модели прямо противоречит сущности моделируемого явления или теоретическим представлениям о сущности моделируемой связи. Такое положение создается из-за наличия тесной связи между факторами (какой-нибудь фактор выражается линейной комбинацией других факторов, включенных в мо- [c.120]
Экономическая интерпретация связей, отраженных в экономико-математических моделях нормативной удельной фондоемкости, производилась посредством технико-экономичес-кого анализа коэффициентов эластичности (в рассматриваемом случае для степенной формы связи — коэффициентов регрессии), показывающих, на сколько процентов в среднем изменяется величина удельной фондоемкости с изменением величины факторного показателя на 1%. Знаки, стоящие перед коэффициентами регрессии в моделях, характеризуют направления влияния каждого производственного фактора-аргумента на изменение величины удельной фондоемкости и соответствуют общепринятым технико-экономическим понятиям, хотя некоторые случаи, видимо, передаются в дополнительном пояснении. [c.527]
Следствием снижения точности является ненадежность коэффициентов регрессии и отчасти неприемлемость их использования для интерпретации как меры воздействия соответствующей объясняющей переменной на зависимую переменную. [c.151]
После проверки значимости каждого коэффициента регрессии обычно проверяется общее качество уравнения регрессии, которое оценивается по тому, как хорошо эмпирическое уравнение регрессии согласуется со статистическими данными. Другими словами, насколько широко рассеяны точки наблюдений относительно линии регрессии. Очевидно, если все точки лежат на построенной прямой, то регрессия Y на X "идеально" объясняет поведение зависимой переменной. В реальной жизни такая ситуация практически не встречается. Обычно поведение Y лишь частично объясняется влиянием переменной X. Возможные соотношения между двумя переменными имеют наглядную графическую интерпретацию в виде так называемой диаграммы Венна (рис. 5.5). [c.130]
Коэффициенты эластичности — это, собственно, относительные величины. Их использование расширяет возможности сопоставления, экономической интерпретации результатов в дополнение к абсолютным величинам — коэффициентам регрессии. [c.137]
| Рис. 9.3. Графическая интерпретация коэффициента детерминации для случая линейной регрессии | 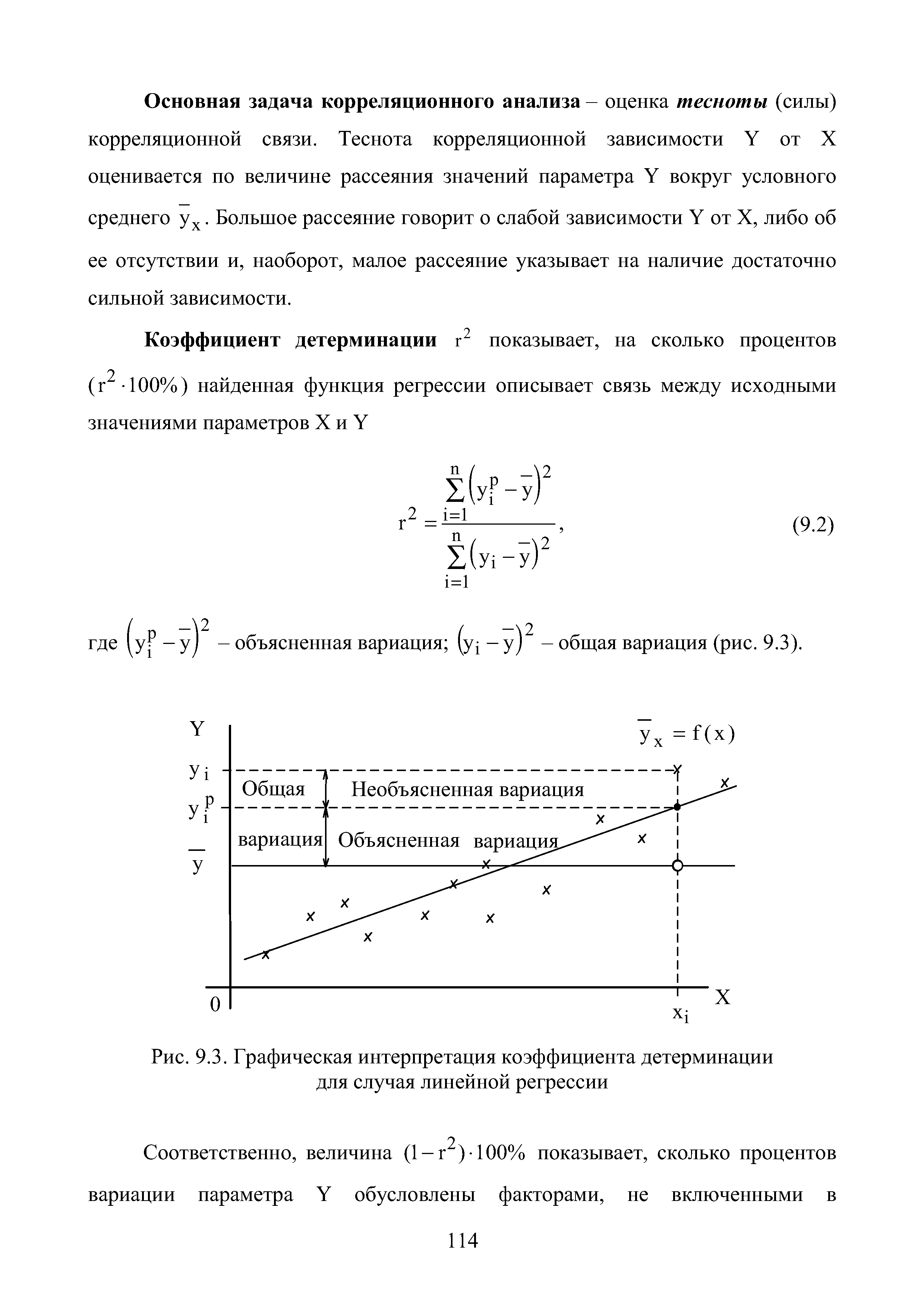 |
Геометрическая интерпретация регрессии и коэффициента детерминации [c.76]
Ввиду четкой интерпретации параметров наиболее широко используются линейная и степенная функции. В линейной множественной регрессии ух = а + 6, хх + b2 х2 +. .. + Ьр хр параметры при х называются коэффициентами чистой регрессии. Они [c.100]
Итак, цель задачи — анализ статистической связи шести параметров полупроводникового прибора. Обозначим эти параметры Xi, xz, x3, 4> хь, хв. Между собой они причинно не связаны. В соответствии с нормами технических условий из общей массы выделялись годные приборы и анализировалась как вся масса приборов, так и годные. Это позволило попытаться уловить различие во взаимосвязи параметров приборов до и после их отбраковки. Эмпирические корреляционные отношения рассчитывались только для годных приборов, поскольку разброс параметров для всей совокупности приборов был настолько велик, что подсчитывать корреляционные отношения не имело смысла. Доверительные интервалы ввиду большого объема выборки подсчитывались по формуле [37]. Сравнение парных коэффициентов корреляции с эмпирическими отношениями использовалось для проверки линейности связи между параметрами. Эмпирическому корреляционному отношению приписывается тот знак, который имеет парный коэффициент корреляции. Связь считается линейной, если корреляционное отношение попадает в доверительный интервал для парного коэффициента корреляции. Может показаться, что мы противоречим высказанному выше утверждению о том, что не существует формальных методов, позволяющих определить форму связи. Однако в данном случае мы говорим не об определении формы связи с целью, например, нахождения параметров уравнения регрессии и дальнейшей интерпретации или экстраполяции в каком-либо виде. Единственная наша забота состоит в том, чтобы парные коэффициенты корреляции (или иные оценки тесноты связи) были действительными характеристиками связи. В табл. 94 приведены в первой строке каждой клетки — парный коэф- [c.188]
Построенное уравнение регрессии в любом случае требует определенной интерпретации и анализа. Интерпретация требует словесного описания полученных результатов с трактовкой найденных коэффициентов, с тем чтобы построенная зависимость стала понятной человеку, не являющемуся специалистом в эконометрическом анализе. В нашем примере коэффициент b>i может трактоваться как предельная [c.106]
Интерпретация коэффициента регрессии как углового коэффициента в линейном уравнении для нелинейной зависимости не годится. Определить изменение У при изменении X на единицу можно с помощью производной (простой или частной), взятой по соответствующему фактору X. Так, для степенного уравнения У = а0Ха производная по X равна [c.136]
При интерпретации коэффициентов регрессии следует иметь в виду, что чем меньше индекс браузинга (зависимая переменная), тем сильнее покупатели склонны демонстрировать поведение, с магазина без определенной Два предиктора с [c.669]
Кроме того, при интерпретации коэффициентов множественной рефессии предполагается независимость факторов друг от друга, что становится невозможным при рассмотрении системы совместных уравнений. Так, в нашем примере уравнение регрессии у = —1,09 + 0,364у2 + 1,192л , показывает, что с ростом х на единицу у возрастает в среднем на 1,192 ед. при неизменном уровне значения у2. Между тем в соответствии с системой одновременных уравнений переменная у2 не может быть неизменной, ибо она в свою очередь зависит от yt. [c.199]
Значения -коэффициента заключены в интервале [—<ю, оо]. Положительное значение / -коэффициента указывает на то, что фактор Xj влияет на х, таким образом, что при изменении Xj в одном направлении (допустим, увеличении) признак х, изменяется в этом же направлении. Отрицательное значение показывает, что Xj и Xj изменяются противоположно. Знак коэффициента влияния получается автоматически в результате решения системы уравнений, связывающей ГуНрд. Содержательная интерпретация коэффициентов влияния Райта как показателей интенсивности влияния по дуге графа аналогична интерпретации / -коэффициентов (как показателей сравнительной силы воздействия факторов) в обычных моделях множественной регрессии. [c.218]
Неопределенность в оценке коэффициентов регрессии при неортогональном планировании затрудняет их физическую интерпретацию уравнение регрессии можно рассматривать только как интерполяционную формулу. В ортогональном же планировании можно придавать определенный физический смысл индивидуальным коэффициентам регрессии. В данном случае уравнение регрессии - не просто интерполяционная формула, а некоторая математическая модель процесса. [c.268]
В статистической литературе встречается следующая интерпретация параметров многомерной регрессионной модели — коэффициент регрессии а,- показывает, на сколько единиц изменяется результативный показатель Y в случае изменения факторного показателя Xi наеди- [c.121]
Интерпретация частного коэффициента регрессии заключается в том, что он представляет ожидаемое изменение величины У, изменяется единицу етаегся постоянной, т.е. управляемой (контролируемой) переменной. В отличие от этого, представляет ожидаемое изменение изменении на единицу, когда. У, остается постоянной. Поэтому названия — частные коэффициенты регрессии, соответствуют действительности. Кроме того, результаты совместного и на суммируются Иначе говоря, если каждую из переменных и изменить на единицу, то ожидаемое изменение значения Убудет равно + [c.661]
Необходимость применения многофакторного корреляционного анализа. Этапы многофакторного корреляционного анализа. Правила отбора факторов для корреляционной модели. Обоснование необходимого объема выборки данных для корреляционного анализа. Сбор и статистическая оценка исходной информации. Способы обоснования уравнения связи. Основные показатели связи в корреляционном анализе и их интерпретация. Сущность парных (общих), частных и множественных коэффициентов корреляции и детерминации. Оценка значимости коэффициентов корреляции. Порядок расчета уравнения множественной регрессии шаговым способом. Интерпретация его параметров. Назначение коэффициентов эластичности и стандартизированных бетта-коэф-фициентов. [c.138]
Для более прозрачной интерпретации отношение средних цен в (16) можно заменить единицей (поскольку оно близко к 1). Тогда видно, что сходимость цен имеет место, если абсолютная мобильность превосходит относительную. При равенстве этих двух видов мобильности коэффициент Джини остаётся неизменным, а преобладание относительной мобильности над абсолютной приведёт к расхождению цен. В данной работе, воспользовавшись соотношением Водона-Ицхаки, / t T t просто рассчитывается из соотношения (16), а не оценивается из регрессии Джини. [c.22]
Получение соответствующего выражения для коэффициента час ной корреляции упрощается, если мы прежде всего выберем нескол ко иной способ интерпретации этого коэффициента. В случае простс регрессии двух переменных мы имеем [c.135]
