Ограниченное решение задачи 140 Ожидания потребителя 760 [c.1178]
ЭВМ семейства СМ, профессиональных персональных ЭВМ. При всех вариантах проектирования АРМ пользователь должен иметь возможность использовать лично устройства, позволяющие ему выполнять должностные функции. К таким устройствам относятся алфавитно-цифровые или графические дисплеи, устройства ввода-вывода, накопители на магнитных носителях. Опосредованное использование могут находить устройства связи ЭВМ между собой и с ЭВМ верхнего уровня, средства передачи и приема информации на расстоянии. Экон. эффект от внедрения АРМ складывается из двух составляющих. Во-первых, это повышение качества управленческих решений, принимаемых с помощью информации, предоставляемой АРМ. Во-вторых, эффект, получаемый за счет снижения трудоемкости выполнения личной работы сотрудников. С помощью АРМ р. целесообразно решать задачи, ограниченные по своим информационным связям на входе и выходе с др. задачами, т.е. локальные в информационном отношении задачи. АРМ р. присущ диалоговый метод решения задач, позволяющий использовать производственный опыт руководителей и специалистов при решении задач с недостаточно четко формализованным алгоритмом. Проектирование и внедрение АРМ р. основывается на принципах проектирования систем обработки данных, основными из которых являются принцип максимальной ориентации на конечного пользователя (реализация данного принципа достигается созданием средств адаптации АРМ к уровню подготовки пользователя и возможностью его обучения (самообучения) непосредственно на данном АРМ) принцип проблемной ориентации — обеспечивает ориентацию АРМ на решение определенного класса задач, объединенных общей технологией обработки данных, единством режимов работы и эксплуатации принцип соответствия информационным потребностям пользователя. К определению состава и функций АРМ р. следует приступать только после установления информационных потребностей пользователя, которые обеспечивают выполнение им возложенных на него функций. Обязательным условием разработки эффективного АРМ р. является совместное участие будущего пользователя и разработчика в этом процессе. Это обеспечивает лучшее осознание всех проблемных ситуаций, стимулирует творческую дея- [c.3]
Термины оптимизация и оптимальный ассоциируются с экономико-математическими методами (ЭММ) и ЭВМ, т. е. с методами и средствами, способствующими наиболее эффективному решению задач планирования и управления. Вместе с тем и в действующей практике, основанной на традиционных методах, руководитель любого уровня управления на предприятии также заинтересован в оптимальном решении вопроса по увеличению выпуска продукции, снижению затрат на производство, использованию капиталовложений и т. Д. Но он пытается этого достичь, пользуясь в основном установившимися принципами общих закономерностей и далеко не совершенными вычислительными средствами. При этом во многих случаях также рассматривается ряд вариантов, хотя и ограниченный, что обусловливается реальными организационными и техническими возможностями. Тем не менее в отдельных случаях не исключено совпадение результатов решения, полученных с использованием ЭММ и ЭВМ и на основе традиционного подхода. [c.377]
В ограничениях обязательно указывается необходимость полного использования действующих мощностей. Необходимый прирост мощности определяется в результате решения задачи. Так как затраты зависят от мощности и степени загрузки оборудования, то задача решается в несколько этапов при варьировании мощности процессов и соответствующих затрат. [c.19]
В приведенной системе ограничений не показан расход этиловой жидкости, который для любой смеси компонентов графически представляет собой параболу. Однако для каждой конкретной смеси компонентов параметры уравнения параболы будут различны. Чтобы не усложнять решение задачи, прибыль от реализации бензинов уменьшается на стоимость этиловой жидкости, исходя из потребного ее количества на доведение октанового числа смеси компонентов до требуемого его значения. [c.77]
Таким образом, целевая функция (2.9) вместе с ограничениями (2.11), (2.17) и (2.18) представляет собой экономико-математическую модель задачи необходимо найти такие значения темпов выполнения работ сетевой операционной модели (количества добавляемых на процессы технологических звеньев), которые обеспечивают строительство объекта в плановые сроки при минимуме затрат на передислокацию строительно-монтажных подразделений. Данная задача относится к классу нелинейных задач целочисленного программирования. Даже в упрощенном варианте организации строительства без учета сменности работ решение задачи представляет определенную трудность. [c.50]
Чтобы выполнять информационную работу, сотрудники компании должны иметь простой доступ к информации. До последнего времени, однако, было принято считать, что цифры являются прерогативой высшего руководства. Некоторые руководители и сейчас предпочитают держать информацию при себе, обосновывая это требованиями конфиденциальности, но большей частью ограниченность доступа к информации вызывалась просто трудностью его организации. Распространение информации требовало времени, усилий и денег. Похоже, что даже сегодня многие не могут забыть, как они задыхались под ворохом ожидавших решения задач, связанных с необходимостью писать специальную программу каждый раз, когда у кого-нибудь возникало желание увидеть результаты чуть-чуть по-другому. Вытаскивать данные с мэйнфрейма было настолько недешево, требовалось так много труда, чтобы попробовать их сопоставить друг с другом, что заказ такого анализа сотрудником компании, имеющим ранг ниже вице-президентского, считался непозволительной роскошью. И даже когда такая информация предоставлялась, она часто бывала противоречивой и ус- [c.35]
В настоящее время в условиях ограниченного числа работников каждой специальности решение задачи эффективного использования рабочей силы (т. е. уменьшение ее простоев) и обеспечение максимальной равномерности ее потребления на протяжении всего хода работ позволяет сократить время, расходы и обеспечить полную занятость квалифицированных кадров. [c.31]
Однако в силу ограничений на размер ресурсов, которыми располагает предприятие и которые оно может выделить для решения задач по созданию новых видов продукции, возникает требование распределения ресурсов на основе определения приоритетов программных целей. [c.216]
Прогнозные расчеты сети строительно-монтажных организаций проводятся с соблюдением ограничений по объемам строительно-монтажных работ по каждому региону сбалансированности объемов подрядных работ с производственными мощностями строительных организаций и предприятий производственной базы обеспеченности мощностей СМО трудовыми ресурсами опережающего роста темпов развития мощностей по сравнению с темпами роста программы оптимизации значения критериального показателя, избранного для решения задачи. [c.49]
Одним из наиболее эффективных и опробованных практикой методов решения задач оптимального планирования является линейное программирование. Оно объединяет теорию и практику решения экстремальных задач, в которых требуется найти совокупность значений переменных величин, удовлетворяющую заданным линейным ограничениям и максимизирующую или минимизирующую целевую функцию этих переменных. [c.33]
При решении задач симплексным методом линейного программирования моделирование заключается в составлении системы линейных уравнений и неравенств, каждое из которых выражает одно из заданных в условии задачи ограничений в виде функций определяемых переменных. [c.34]
При решении задачи по размещению перевалочной нефтебазы должны быть соблюдены следующие ограничения [c.82]
Учитывая, что развитию нефтедобывающих районов предшествует подготовительный — инкубационный — период, определяющий объемы добычи нефти по району, базирующиеся на геолого-технических характеристиках месторождений, период активных вложений можно рассматривать как самостоятельный этап развития. Ограничениями при моделировании развития района в данном случае могут быть, кроме объемов добычи нефти, число вводимых эксплуатационных скважин по месторождениям и годам их разработки, система разработки месторождений и объемы закачки для поддержания пластового давления и т. д., т. е. основные параметры, позволяющие рассчитать потребность в транспорте, численности населения, объемов капитальных вложений и т. д. При этих условиях в качестве одного из методов решения задачи по выбору рациональной организации района можно принять агломерационную сетевую модель развития района с учетом очередности проведения технологических и организационных процессов. [c.64]
Первая стадия — выдача задания на проектирование — в основном предопределяет весь процесс проектирования и конечный результат работы проектной организации. К сожалению, этой стадии часто не придают должного значения и в результате рождаются проекты с низкими технико-экономическими показателями, неэкономичные, а иногда и неосуществимые. При разработке заданий необходим тщательный анализ возможных путей решения задачи. Экономические изыскания на этой стадии не требуют детальных расчетов, но проработки с определенными ограничениями и допущениями обязательны, так как только они дают возможность осмысленно представить масштабность будущих решений и оценить реальность их осуществления. [c.100]
В ограничениях обязательно указывается мощность действующих (технологических) процессов. Необходимый прирост мощностей получается в результате решения задачи. Так как величина затрат с/ зависит от мощности и степени загрузки оборудования, то задачу приходится решать в несколько этапов, варьируя мощность процессов и соответственно величину затрат. [c.88]
Найдя множество допустимых решений задачи (1.5), определим допустимые пределы нарушения ограничений (1.2) и (1.4). Это можно определить в диалоге ЛПР (технолога-оператора процесса). Пусть di=1,0 d2=0,5 d3=1,0. [c.48]
Симплекс-метод представляет собой технику решения задач с ограничивающими факторами при помощи компьютера (соответствующие расчеты можно сделать и вручную, но это очень трудоемко, даже при относительно несложных задачах). Будучи ограниченным только аппаратными или программными возможностями (т.е. особенностями прикладной программы или объемом памяти компьютера), симплекс-метод позволяет решать задачи с огромным количеством товаров/услуг и ограни- [c.370]
На рис. 8.4 представлено графическое решение задачи линейного программирования. Известно, что все ограничения, изображенные на рис. 8.3, являются неравенствами со знаком "<". Какова область допустимых значений [c.380]
Как видно, описанный здесь метод решения, основанный на полном переборе вершин, является значительно более простым л эффективным, нежели непосредственное использование метода множителей Лагранжа. В то же время не следует считать, что решение задач линейного программирования является простым делом, состоящим просто в полном переборе вершин множества допустимых значений переменных. Для того чтобы понять это, достаточно заметить, что вершина множества допустимых точек (в том случае, когда это множество имеет внутренние точки) в задаче (4.22) — (4.24) связана с обращением в равенства п ограничений из их совокупности (4.23), (4.24). Таким образом, вообще говоря, число вершин множества (4.23), (4.24) может равняться числу различных сочетаний по п ограничений из общего числа т + п. Число различных сочетания [c.51]
Условия (4.36), (4.37) означают, что соотношение vj > 0 влечет равенство в J -M ограничении прямой задачи на оптимальном решении х с другой стороны, если в /-м ограничении на оптимальном решении х выполняется строгое неравенство, то Vj =0. В последнем случае величину bj можно уменьшить без изменения оптимального решения и значения критерия. Поскольку во многих экономических задачах величины bj (] = = 1,. .., /п) характеризуют объем тех или иных производственных ресурсов, соотношение Vj = 0 демонстрирует избыточность /-го ресурса. [c.56]
Таким образом, значения оптимального решения двойственной задачи характеризуют устойчивость по отношению к изменениям правых частей ограничений. Это определяет их важную роль в экономическом исследовании при анализе последствий изменения правых частей задачи. Поскольку величины v- (j = = 1,. .., иг) оценивают существенность изменения критерия при изменении соответственного ограниченного ресурса, их часто называют объективно обусловленными оценками данного ресурса (а также оптимальными или двойственными оценками). Как мы увидим в заключительной главе книги, объективно обусловленные оценки могут использоваться и при решении задач ценообразования. [c.56]
Рассмотрим теперь отдельное предприятие. Показатели, с помощью которых оценивается продукция предприятия, передаваемая за его пределы, должны отражать важность продукции предприятия в решении задач, стоящих перед отраслью, к которой оно принадлежит, перед экономическим районом, в котором оно расположено, и перед народным хозяйством в целом. Интересы экономических систем более высокого уровня отражаются прежде всего в плановом задании, задающемся как в натуральных, так и в стоимостных показателях. В модели пла-, новое задание отражается в виде ограничений, которые для натуральных показателей имеют вид (6.16), а для стоимостных имеют, например, вид [c.128]
Еще одним эффективным средством решения задач управленческого учета является линейное программирование. В экономике существует много способов использования ресурсов таким образом, чтобы получить требуемую чистую прибыль. Метод линейного программирования позволяет наилучшим образом распределить имеющиеся ресурсы для изготовления продукции, зная их количество и стоимость. Почти всегда ограниченные факторы или дефицитные ресурсы налагают определенные ограничения на возможные действия руководите- [c.213]
| Рис. 8.5. Геометрическое решение задачи линейного программирования с ограничениями | 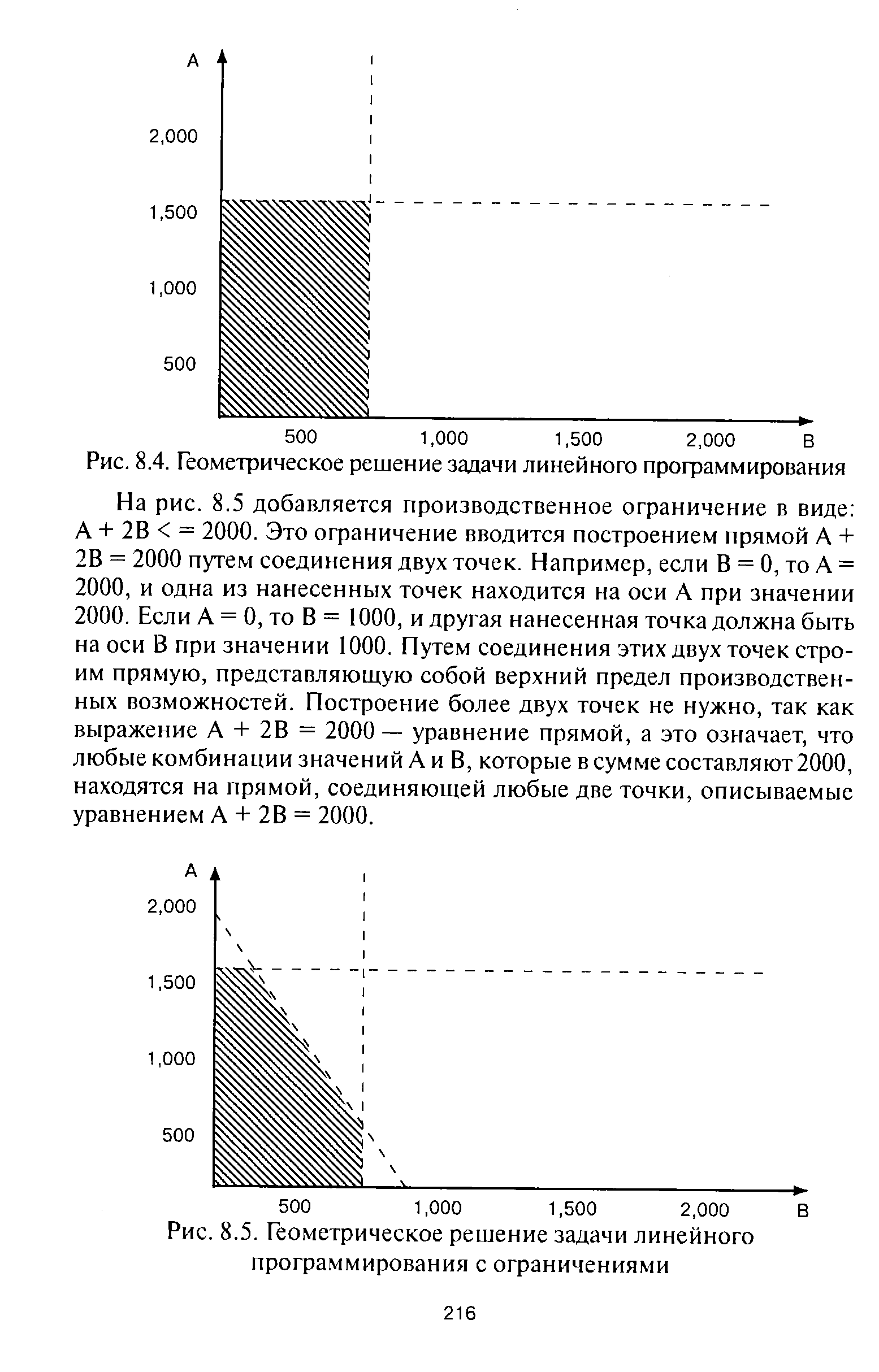 |
Все ограничения, отражающие экономический процесс, должны быть непротиворечивыми, т. е. должно существовать хотя бы одно решение задачи, удовлетворяющее всем ограничениям. [c.104]
Разработка направлений перспективного развития предприятия гредусматривает рассмотрение множества допустимых вариантов и. выбор из них оптимального. Эта работа является многоэтапной, и в процессе ее выполнения на предприятии решаются различные инженерные и технико-экономические задачи, связанные с большим объемом вычислений. Вариантные разработки, которые выполняются коллективом предприятия, служат исходной информацией для решения комплексной задачи в масштабе отрасли. В условиях функционирования АСУП появляются все предпосылки для много-вариантного решения задач заводского перспективного планирования, в то время как традиционная практика в силу большой трудоемкости этих работ позволяет рассматривать ограниченное число вариантов. [c.419]
Критерии и ограничения тесно взаимодействуют при решении геоэкономических задач. Они функционируют как единая двучленная система. Но роль у каждого из них - своя. Ограничения бракуют варианты, не вписывающиеся в существующие условия. С помощью же критерия из оставшихся для рассмотрения вариантов отбирают наивыгоднейший. Взятый сам по себе, без учета ограничений, критерий мог бы увести решение задачи в сторону идеалов, нереальных для рассматриваемых условий (рис. 2.2). [c.31]
Для подавляющего большинства производственных задач основным является критерий экономической эффективности. Попытки принимать в качестве решающего критерия чисто технические параметры (скажем, рост мощности, скорость выполнения процесса или повышение его надежности) закономерны лишь в случаях, когда точно известно, что максимальное их значение автоматически приносит наибольший экономический эффект. Чаще, однако, абсолютной уверенности в этом не бывает. Организационные параметры можно принимать в качестве критериев также лишь для ограниченного числа задач они либо трудно определимы численно, либо слишком узки. Как правило, нужно стремиться переводить их в экономические оценки. Гораздо большего внимания заслуживают социальные критерии - нередко действительно наиважнейшие. К сожалению, наукой пока еще плохо проработаны вопросы о содержании социальных критериев, способах численной оценки, а также сопоставления их между собой и с экономическими критериями. Показатели экологической безопасности решения важны и становятся все более значимыми ввиду критического состояния природной среды. Трудности, связанные с использованием экологических характеристик в качестве решающих критериев эффективности решений связаны с неизученностью сложного механизма возникновения экологических последствий. [c.219]
Преобразование плановой экономики в рыночную сопровождается сменой приоритетов в формировании структуры народного хозяйства. Для решения задачи стабилизации и оживления экономической конъюнктуры должны быть определены отрасли - мультипликаторы экономического роста. В работах известных ученых Р.И. Шнипера, Д.С. Львова, А.И. Татаркина и др., этому вопросу уделялось особое внимание. При ограниченности инвестиционных средств важно всесторонне обосновать приоритетные направления, с учетом их воздействия на макроструктуру в целом. При этом учитываются не только экономические, но и социальные аспекты. [c.182]
Шер А.П. Решение задачи математического программирования с линейной целевой функцией в размытых ограничениях //Автоматика и телемеханика 1980г.,№7// [c.50]
Заметим, что на сети, изображенной на рис. 16, груз из пункта / может быть перевезен в пункт IX по разным дорогам. Если бы мы захотели перейти к матричной форме транспортной задачи, то нам надо было бы заранее решить, по какому из маршрутов мы повезем груз. Если пропускная способность каждой из дорог не ограничена, то переход к матричной форме не вызовет затруднений при относительно простой сети. В более сложных сетях этот вопрос можно решить с помощью специально предназначенных для этого алгоритмов. Если же пропускная способность некоторых участков сети дорог ограничена, то возникают осложнения следующего рода. Пусть по участку дороги от пункта IV до пункта V можно провезти не более 30 единиц груза. Но по этой дороге мы можем везти груз и из пункта / в пункты V, VIII и IX, и из пункта /// в пункт VI. Спрашивается, на какие из перевозок мы должны наложить ограничения при переходе к матричной постановке По-видимому, на все вместе. Но, с другой стороны, если возможности дороги между пунктами IV и V будут исчерпаны, часть грузов можно будет перевозить по другим дорогам. Однако при этом изменится величина затрат на перевозки единицы груза, так что в матричной постановке величина сц оказывается зависимой от ху, и задача становится нелинейной. Хотя все эти трудности перехода к матричной постановке задачи перевозки грузов все-таки можно преодолеть при помощи разнообразных искусственных приемов, многие предпочитают решать задачи в сетевой постановке, не переходя к матричной. Алгоритмы решения транспортной задачи были преобразованы к форме, пригодной для решения задач сразу на сети. К сожалению, эти алгоритмы более громоздки, чем алгоритмы решения транспортной задачи в матричной постановке. Есть и другие недостатки сетевой постановки задачи, есть и ряд дополнительных преимуществ, [c.160]
Здесь номера строк не являются входными данными, они приводятся для того, чтобы мы могли идентифицировать каждое из выражений в распечатке решения задачи не надо вводить и условие неотрицательности оно заложено в программе изначально). Конкретный формат ввода целевой функции и ограничений определяется требованиями конкретного программного пакета. Многие пакеты прикладных программ, такие как LINDO (которым мы воспользуемся), позволяют вводить данные в "естественном" формате, т.е. так, как мы только что их записали. [c.371]
Природа выполняемых задач. Стандартные, повторяющиеся задачи, которые имеют множество ограничений (например, технологических), а также те, которые требуют высокой скорости и точности выполнения, по мнению Хопвуда (1974), лучше решаются в условиях авторитарного стиля управления, нежели задачи более широкого плана, требующие большей гибкости в подходах, сформулированные расплывчато. Однако Хопвуд отмечает, что эффект участия в управлении даже при решении задач второго типа будет "тем более коротким и узко экономическим,. ..чем выше авторитарность стиля руководства". Из этого следует, что увеличение степени участия сотрудников в управлении не связано напрямую с улучшением их мотивации и удовлетворенности от работы. [c.790]
Методы, основанные на использовании множителей Лаграи-жа, позволяют решать задачи оптимизации, если число ограничений не слишком велико, а также анализировать общие свойства экономико-математических моделей. Все же они не стали основным средством решения задач оптимизации в силу ряда специфических особенностей экономических задач, главные из которых состоят в большой размерности экономических задач и в возможности формулировать многие экономико-математические модели на основе линейных соотношений. Читатель убедится в этом, прочитав следующие главы книги. [c.49]
Методы линейного программирования. Первые исследования по постановке и разработке методов решения линейных оптимизационных задач были проведены в тридцатые годы Л. В. Канторовичем. В 1939 г. им была опубликована книга Математические методы организации и планирования производства , в которой впервые был ш сдложен эффективный метод решения задач оптимизации для моделей с линейными ограничениями и линейным критерием. Однако достоинство книги состояло не только в этом — в пей было показано, что модели экономических систем широкого класса могут быть достаточно точно построены на основе использования линейных соотношении. В дальнейшем эти идеи получили широкое распространение, и в настоящее время липейиые модели и методы оптимизации в таких моделях составляют основу, на которой базируется исследование прикладных экономических задач. [c.50]
Декомпозиционные методы основываются па том факте, что для выбора оптимального плана необходимо знать информацию об ограничениях на принимаемые решения лишь в окрестности оптимальной точки. Поэтому для решения задачи оптимизации Центр может удовлетвориться частичной информацией, получаемой от предприятий в процессе взаимодействия. Для получения необходимой информации Центр может, например, сообщать предприятиям цеыы на ресурсы и требовать в ответ оптимальные для предприятий варианты затрат ресурсов и выпуска продукции. В других декомпозиционных схемах Центр сообщает предприятиям варианты распределения ресурсов, они же в ответ сообщают свои оценки этих ресурсов. В любом случае при построении декомпозиционных схем важнейшим является вопрос о том, какие критерии нужно назначить отдельным подсисте- [c.350]
Линейное программирование (linear programming) — раздел математического программирования, посвященный методам решения задач об экстремумах линейных функций на множествах, задаваемых системами линейных неравенств и равенств. Используется менеджерами для принятия решений в ситуациях с ограниченными ресурсами. [c.239]
