| Рис. 18. Граф (дерево) решения задачи. | 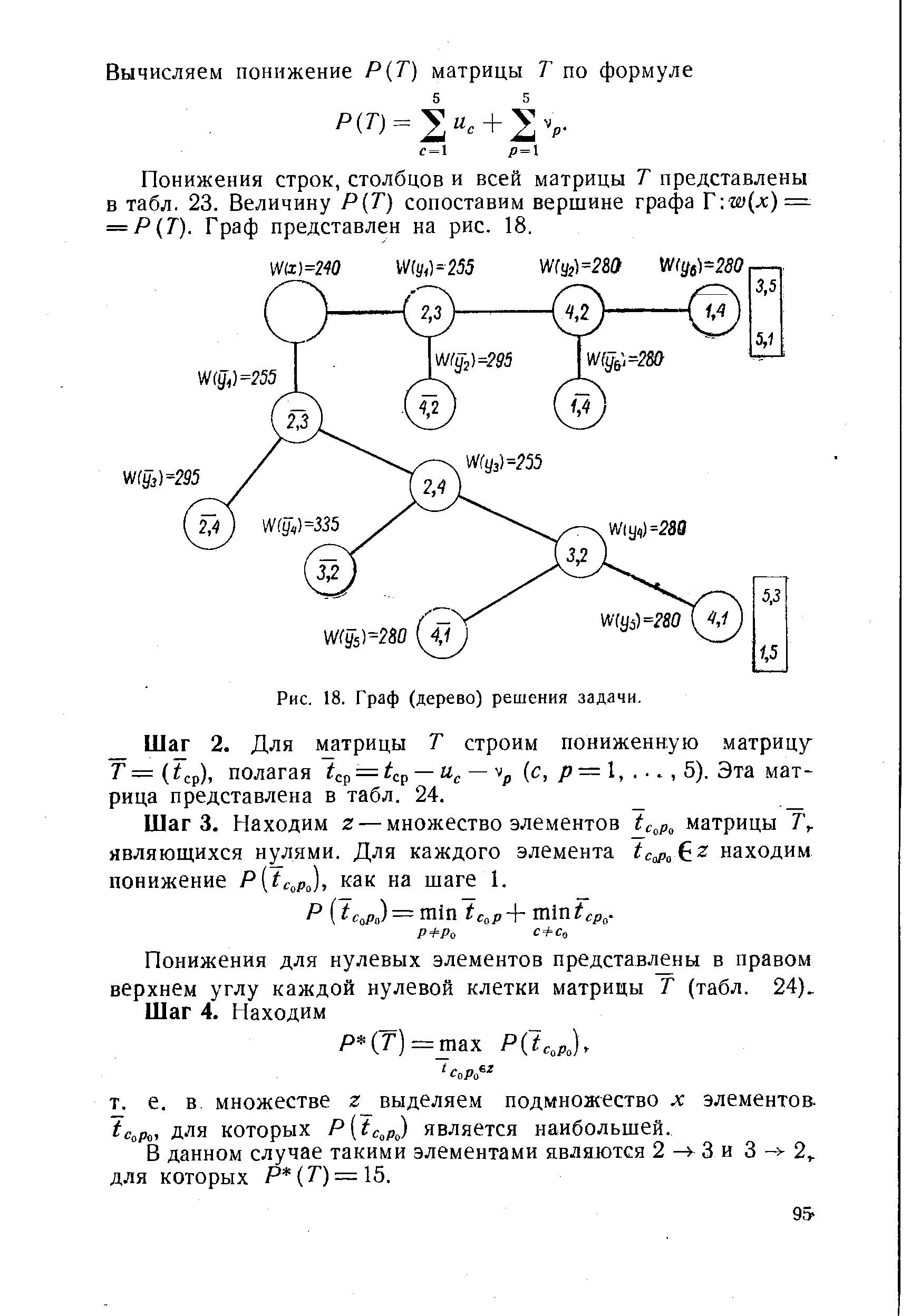 |
ДЕРЕВО РЕШЕНИЙ" - структурная модель процесса принятия решений, включающая его элементы по уровням (цели, задачи, рабочие мероприятия) и связи между ними (включение или подчиненность). Является инструментом программно-целевого управления. Формирование Д.р. включает выбор главной цели и ее декомпозицию до уровня рабочих мероприятий, с решения которых можно начинать работу по достижению поставленной цели. Количественная оценка элементов Д.р. с использованием коэффициентов значимости (весомости) позволяет рационально распределить ресурсы, выделяемые для достижения заданной цели. [c.67]
Особенностью программно-целевого метода планирования является построение двух графов — дерева целей и дерева ресурсов . Дерево целей изображается в виде уровней и ветвей более низких уровней. Решение задач, расположенных на более низких уровнях и ветвях, обеспечивает выполнение задач более высоких уровней. При этом средства, необходимые для достижения целей верхнего уровня, сами являются целями для каждого последующего нижнего уровня. При наличии нескольких целей на основе экспертных оценок устанавливают их приоритетность. Ключевые проблемы выявляются также с помощью многовариантных расчетов на ЭВМ. На их разработку направляются наибольшие силы и средства. Для достижения важнейших целей эти силы и средства отражаются в программах развития отрасли, производственно-территориальных комплексов. [c.77]
Процесс решения задачи применительно к определению оптимального порядка запуска предметов на линию основан на переходе от множества всех последовательностей обработки различных предметов к более мелким подмножествам и вычислении для каждого из них нижней границы затрат времени на переналадки. Все множество последовательностей запуска различных предметов на линию представляется в терминологии теории графов вершиной дерева, подмножества — как узлы дерева, а процесс разделения подмножеств — как разветвление дерева. [c.82]
Алгоритм решения задачи основан на постепенном построении графа (дерева) Г, сопоставлении узлам графа некоторой числовой характеристики w (нижней границы затрат времени на переналадки оборудования) и развитии того узла графа, для которого эта величина w меньше по сравнению с другими узлами. Каждый этап этого алгоритма соответствует нахождению [c.82]
При решении задач большого размера построение всего дерева [c.30]
При решении задач организации эффективного доступа к данным индексы больших размеров преобразуют в иерархию индексов небольших размеров. Один из способов реализации таких индексных структур состоит в использовании й-деревьев, листьями которых являются ссылки на документы. [c.520]
См. также Алгоритм управления, Дерево решений, Лицо, принимающее решения, Многошаговые процессы принятия решений, Область допустимых решений, Планово-экономическая задача, Последовательные методы принятия решений, Решение игры, Системы поддержки решений, Теория рейхе)чий, Экономико-математический анализ решения оптимизационных задач. [c.311]
Обнаруженные соотношения, закономерности находят применение в самых различных областях экономики. С их помощью можно решать задачи по построению наилучшего плана перевозок продукции от поставщика к потребителям, вырабатывать маршруты различных перевозок, рассчитывать наилучшее распределение рабочих по машинам на производстве и т.д. На Т.г. основаны, в частности, сетевые методы планирования и управления, использование в различных разделах экономико-математических методов таких средств, как дерево целей, дерево решений. [c.356]
ДЕРЕВО ЦЕЛЕЙ И ЗАДАЧ - развернутая, распределенная по уровням совокупность целей и задач экономической программы, построенная по логической схеме цели - программы - задачи, которые надо решить для достижения этих целей,— мероприятия, обеспечивающие решение задач,- ресурсы, необходимые для проведения мероприятий . Дерево целей и задач используется в программно-целевом планировании и управлении. [c.72]
Типичная задача для условий риска каким должен быть размер строящегося предприятия. Очевидно, таким, чтобы удовлетворить будущий спрос. Основные варианты решения связаны с факторами спроса и состоянием рынка для производимых товаров. Для этого будущий рынок должен быть классифицирован (например, как благоприятный и неблагоприятный). Методика, которая может быть эффективно использована в принятии плановых решений по мощности с неопределенным будущим, — это теория решений. Теория решений предполагает использование как таблиц, так и деревьев решений, которые требуют спецификации альтернатив и состояния природы. Для ситуации планирования мощности состояние природы — это обычно будущий спрос или благоприятный рынок. Для установленных вероятностей вариантов состояния природы можно принять решение, которое максимизирует ожидаемый результат альтернативы. Это осуществляется следующим образом с использованием дерева решений [c.191]
Наиболее широко используемым методом для решения разнообразных задач менеджмента является метод дерева решений, или метод платежной матрицы. Этот метод используется для ответа на вопрос, какая из альтернативных Стратегий поведения в наибольшей степени соответствует достижению поставленных целей в условиях неопределенности внешней среды или риска. Метод может помочь менеджерам принимать управленческие решения в подавляющем большинстве ситуаций, практически возникающих в их работе. Метод имеет три преимущества [c.218]
Построение дерева рассмотрим также на примере решения задачи тактического планирования. Выделение только двух состояний внешней среды — благоприятного и неблагоприятного—далеко не единственный и не лучший способ оценки внешней среды, который применяется лишь в случаях, когда информация о среде ограничена. Альтернативных вариантов стратегий в общем случае может быть много. И это позволяет уточнить решение задачи. [c.223]
Отметим, что здесь решения должны приниматься дважды, причем решение о принятии того или иного варианта строительства должно быть принято на основе уже известных к тому времени результатов дополнительных исследований. Это определяет последовательность решения задачи, в частности, последовательность узлов принятия решений в дереве для этой задачи. Построим дерево решений и рассчитаем на его основе значения ЕМУ (рис. 9.5). Расчет ведем справа налево — от известного к искомому (тыс. руб.) [c.227]
Оценка риска методом "дерева решений" представляет собой моделирование задачи выбора вариантов решений графическим способом. Построив "дерево" из ветвей или путей развития возможных событий, оценивают каждый путь и выбирают наименее рискованный. Данный метод представляется наиболее трудоемким и неточным из-за опасности не учесть при построении "дерева" какой-либо путь развития событий. [c.289]
Основываясь на системном подходе к анализу систем примеры таких деревьев решений можно представить на любом иерархическом уровне управления нефтегазового производства производственное объединение, завод, цех, бригада государственно-административной - федерация, область, район, населенный пункт и т.д. Такие деревья целей и решений могут строиться не только в соответствии с иерархией задач управления на предприятии, компании, акционерном обществе и др., но и в сочетании с другими признака- [c.20]
На рисунке 6.8, рассматриваемая задача представлена в виде дерева решений. Предполагается, что спрос может оказаться высоким или низким. Дерево решений имеет два типа вершин решающие вершины (П ) и случайные вершины (О ). Таким образом, начиная с вершины 1 (решающей вершины), необходимо принять решение относительно способа разработки. Вершина 2 является случайной, из нее выходят две ветви, соответствующие низкому и высокому уровням цен в зависимости от сложившейся ситуации на рынке. Каждая из этих ситуаций представлена соответствующим значением вероятности ее реализации. Вершина 3 также является случайной, из нее выходят две ветви, обозначающие разные уровни цен. [c.217]
Все задачи, решаемые с помощью деревьев решений, могут быть сведены к следующим трем типам [c.223]
Изучаемую систему представляют в виде иерархии, которая изображается графом связей (в простейшем случае типа дерево) между элементами уровней - первый и очень важный этап решения задачи. [c.253]
Новые языки для решения задач искусственного интеллекта предоставляют новые, более гибкие возможности передач управления от модуля к модулю. Идея заключается в том, что модуль при передаче управления другому модулю сохраняет свое состояние. При этом любой программный модуль не обязан возвращать управление тому модулю, от которого оно было получено. Таким образом, управление не только движется вверх и вниз по дереву иерархии, но и передается от одного модуля к другому в любом порядке. Когда приостановленный модуль вновь получает управление, его выполнение начинается с точки остановки и со значениями внутренних параметров, которые имели место в момент остановки. Он может получать управление от любого другого модуля по инициативе последнего и передавать управление также любому другому, запоминая свое состояние в момент передачи. Такие равноправные программные модули называются сопрограммами в отличие от подпрограмм в строго иерархической структуре управления. [c.516]
С помощью этого метода решается целый ряд задач, когда имеются два или более последовательных множества решений, причем, последующие решения основываются на результатах предыдущих состояний среды, т.е. появляется цепочка решений, вытекающих одно из другого. Подобные задачи проще решать с использованием дерева решений, которое представляет собой графическое изображение последовательности решений и состояний среды с указанием соответствующих вероятностей и выигрышей для всевозможных комбинаций. [c.124]
С помощью дерева решений рассмотрим задачу выбора оптимального проекта реконструкции фабрики — химчистки. [c.128]
Еще одним важным методом исследования риска является моделирование задачи выбора с помощью дерева решений. Метод основан на графическом построении вариантов решений. Его используют тогда, когда решение принимается поэтапно или когда с переходом от одного варианта решения к другому меняются вероятности. [c.72]
Постройте дерево решений данной задачи (рис. 2.2). [c.84]
Дерево решений — граф, схема, отражающие структуру задачи оптимизации многошагового процесса. Ветви дерева отображают различные события, которые могут иметь место, а узлы (вершины) —точки, в которых возникает необходимость выбора. Причем узлы различны [c.100]
Постройте дерево решений для рассматриваемой задачи. [c.520]
При инновационном проектировании разрабатывают довольно сложные дерево целей , дерево критериев , дерево относительной важности задач , дерево решений и другие модели. С помощью морфологического анализа можно рассмотреть множество вероятных функциональных возможностей применения объекта, возможных стратегий, целей и основных точек зрения. Выполненный таким образом анализ позволяет определить общую полезность какого-либо новшества, оценив, насколько оно удовлетворяет отдельным элементам общей системы потребностей. Новшество и его инновация могут содействовать реализации всего одной функциональной возможности, которая, в свою очередь, имеет всего одно или несколько потенциальных областей применения объекта. [c.256]
Взаимосвязанность и взаимозависимость категорий цели и альтернативы более наглядно можно проиллюстрировать с помощью метода дерево решений 1, который предполагает разработку вариантов достижения целей различных уровней дерева целей, при этом дерево целей всегда можно развивать до такой степени детализации, чтобы на последнем уровне находились задачи, которые уже невозможно рассматривать в качестве целей. [c.130]
На втором занятии преподаватель совместно со слушателями анализирует полученные расчетные данные и исправляет возможные ошибки. Далее строят графосхе-мы и получают вероятностные оценки. Затем на основе расчетов ожидаемого дохода по конечным ветвям дерева решений задачи слушатели выбирают оптимальную стратегию развития отрасли. Завершается занятие коллективным обсуждением полученного оптимального решения. Поскольку разработанный прогноз относится к исследовательским (поисковым), он требует применения комплексного метода, сочетающего экспертные и экстра-поляционные методы. [c.84]
ДЕРЕВО РЕШЕНИЙ [de ision tree] — граф, схема, отражающая структуру задачи оптимизации лтогошагового процесса при-иктя.решений. Применяется в динамическом программировании и в других областях для анализа решений, структуризации проблем. Ветви дерева отображают различные события, которые могут иметь место, а узлы вершины) — состояния, в которых возникает необходимость выбора. Причем узлы различны — в одних выбор из некоторого набора альтернатив осуществляет сам решающий (руководитель), в других узлах выбор от него не зависит. В таких случаях говорят, что выбор делает "природа", а руководитель может только оценить вероятность того или иного ее "решения". [c.77]
В теории разработки управленческих решений выделяют следующие методы аналитические, статистические, матричные, эвристические, активизирующие методы, экспертные методы, методы сценариев и метод дерева решений. Каждый метод (как процесс). основан на использовании специально разработанных моделей (явлений). Так, аналитические методы разработки УР основаны на моделях, представляющих требуемый набор аналитических зависимостей, эвристические — используют модель американцев Саймона и Ньюэла по стимулированию мышления при разработке УР и т. д. Каждая модель РУР должна периодически проверяться на достоверность, точность и эффективность. Проверка на достоверность необходима для соизмерения ее результатов с требованиями сегодняшнего дня. Основная задача каждой модели — облегчить какую-либо деятельность за счет формализации ряда процессов, входящих в данную деятельность. Всякое упрощение вносит ошибку в конечный результат. Приемлемость ошибки и выявляет проверка на достоверность. Точность определяется соответствием моделируемых процедур и операций при РУР реальным процессам и операциям. Чем точнее модель, тем она дороже. Точная модель не дает гарантии разработки эффективного решения, так как человек может [c.263]
Кроме использования платежной матрицы для решения данного типа задач, как уже указывалось, можно строить дерево решений. Например, для рассматриваемой в прщмере 9.1 задачи дерево имеет следующий вид (рис. 9.2). [c.221]
EVPI = 385 х 0,45 + 420 х 0,35 + 455 х 0,20 - 385 = 26,25 руб. Дерево решений этой задачи имеет следующий вид [c.224]
При теоретико-графовом подходе (см., например, [13—15]) используется формализованное представление модели проблемной среды в виде графа, узлы которого соответствуют возможным состояниям среды, а дуги — возможным действиям, преобразующим одно состояние в другое. В качестве решающих процедур используются эвристические стратегии поиска пути на графе, строящемся в процессе формирования решения задачи в виде дерева с основанием в начальном узле. [c.370]
Здесь я не буду обсуждать вопрос о том, как распознавать леммы1) и как получать их аналогии2) вместо этого я только хочу отметить, что леммы могут эффективно применяться и без использования планирующего языка, который требует возврата к началу в случае неуспеха в доказательстве. Предположим, что мы каким-то образом получили G(L ),. .., G(Lj). Типичный планировщик упорядочил бы леммы G(Lj), например G(Li), G(L2) и т. д., пытаясь последовательно разрешать их и останавливаясь, если какую-нибудь лемму не удается решить. В противоположность этому мы только делаем попытки найти решение для каждой из лемм G(Lt). Если мы получаем решение, мы добавляем G(Li) к базе данных (в качестве теоремы)3) и продолжаем процесс для следующей леммы. Если решение получить не удается, выбирают любую другую лемму. В худшем случае мы потратим некоторое дополнительное машинное время. Каждая полезная лемма G(L,-) уменьшает число шагов в решении задачи РА и может уменьшить длину дерева поиска решения. Таким образом, леммы могут помочь в сокращении поиска решения. Заметим, однако, что полученное решение G(Lj) необязательно будет использовано в решении задачи РА. Это всего лишь вероятно. Следовательно, мы не связаны свойством возврата к началу при неуспехе , характерным для последовательной планирующей логики. [c.477]
В практике системного анализа подобных вероятностных задач планирования при их оптимизации распространение получил графоматематический метод дерево решений , в основе которого лежат динамическое программирование и теория статистических решений1. [c.74]
Название метода ПАТТЕРН состоит из первых букв английских слов, означающих помощь планированию посредством количественной оценки технических данных. Сущность его состоит в том, что изучаемая проблема расчленяется на ряд подпроблем, отдельных задач и элементов, которые выстраиваются в "дерево решений". Определяются коэффициенты важности каждого элемента, подлежащих экспертной оценке. Оценки отдельных экспертов подвергаются открытому обсуждению. Данный метод извлекает пользу от делового взаимовлияния экспертов, не исключая отрицательных последствий конформизма. [c.180]
