Зная эти предположения, мы можем определить равновесную стоимость опциона. Если действительная цена опциона отличается от цены, полученной в модели, мы можем установить безрисковую хеджированную позицию и получить прибыль большую, чем краткосрочная процентная ставка. По мере вступления на рынок участников арбитражных сделок сверхприбыль будет постепенно вытеснена, и цена опциона сравняется со стоимостью, приведенной в модели. [c.662]
Таким образом, короткую позицию в опционах нужно последовательно приспосабливать к изменениям цены акций и изменениям во времени для сохранения безрисковой хеджированной позиции. Условия модели это позволяют но в реальной жизни трансакционные издержки делают непрактичным длительное приспособление короткой позиции. Даже здесь риск, который появится в результате изменений цены акций или с течением времени, будет невелик. Более того, от него можно избавиться. На практике возможно сохранение хеджированной позиции, которая является приблизительно безрисковой. Арбитражные сделки гарантируют, что прибыль при этой позиции будет краткосрочной и безрисковой. [c.663]
На практике управляющие фондами применяют неагрессивные методы динамичного хеджирования. Они не предусматривают необходимости торговли портфелем из наличных акций. Вместо этого портфель, в целом, подстраивается к тому, какой должна быть текущая дельта, величина которой диктуется моделью использования фьючерсов на индексы акций и иногда пут-опционов. Одно из преимуществ метода использования фьючерсов состоит в том, что они имеют низкие операционные издержки. [c.222]
Одним из лучших примеров является японский рынок варрантов периода 1987 — 1993 годов. Японские варранты являются долгосрочными опционами колл, и по разным причинам они торговались с существенным дисконтом от теоретической стоимости, которая определялась по модели Блэка-Шоулза. В то время этому расхождению придумали удобное объяснение, согласившись с тем, что модель неприменима к опционам с четырьмя или пятью годами жизни. Основные участники рынка являлись спекулянтами, которые очень редко понимали теоретические стоимости, дельты и гаммы. Они просто покупали варрант, потому что рынок шел наверх. Ликвидность этих инструментов была огромна по сравнению с той, что наблюдалась на других рынках опционов, и часто можно было купить варранты стоимостью до 20 миллионов за один день. Большой спекулятивный интерес и отсутствие всякого значительного хеджирования предполагали возникновение бесчисленных аномалий и сохранение их на целые годы. Наиболее заметное неверное оценивание возникало тогда, когда варранты шли в деньгах. Спекулянты покупали варранты, очень далеко вне денег, по любой цене, тем самым поднимая подразумеваемую волатильность до 40%. Если им везло, а в конце 80-х им везло часто, цена основного инструмента росла, увеличивая цену варранта зачастую в пять или шесть раз от первоначальной стоимости. Обрадованные такими большими компенсациями за риск, спекулянты распродавали их частями, часто толкая цену от равноценных скидок к большим скидкам от теоретических стоимостей. Цены таких варрантов в деньгах были часто ниже тех цен, которые были получены на основе моделей, использовавших нулевое значение волатильности. Эти инструменты давали возможность хеджерам создавать длинные по волатильности портфели по отрицательной стоимости, а это означало, что даже в самом худшем случае при возникновении нулевой волатильности в результате все равно будет прибыль. И все это происходило, когда японский рынок ценных бумаг переживал один из самых волатильных периодов в своей истории. [c.196]
В приведенном выше примере одновременная покупка волатильности при 15% и продажа при 22%, скорее всего, приведет к прибыли, но что если подразумеваемые волатильности оказались ближе, скажем, 15% и 17% соответственно В таком случае, вероятнее всего, мы не сможем гарантировать прибыль. В большинстве случаев на биржевых опционных рынках можно найти такие опционы, которые обладают одинаковыми циклами истечения срока, обращаются на акции с различными ценами и имеют разные подразумеваемые волатильности. Первоначально многие профессионалы, наблюдающие эти различия, увеличивали хеджированные позиции, такие, как позиции, описанные выше. На ранних стадиях опционных биржевых рынков, когда аномалии были еще большими, многие из таких позиций приносили прибыль, но некоторые создавали убыток. Со временем протяженность аномалий сокращалась, но они все еще существовали. Некоторые профессионалы полагают, что модель неверна и что подразумеваемая волатильность не годится для измерения стоимости. Другие считают, что допущение логнормального распределения не является верным, и исследования в этой области все еще продолжаются. Однако некоторые ученые доказали, что аномалии могут быть объяснены, если отойти от предположения о постоянстве волатильности. Почти каждый согласится с тем, что изменяющаяся волатильность на некоторых рынках связана с ценой основного инструмента. Когда цена акции падает (растет), волатильность часто увеличивается (уменьшается). Было показано, что сочетание этих и других аспектов в модели Блэка-Шоулза совместимо с различными ценами акций, имеющих разные подразумеваемые волатильности. Поэтому модель все еще может быть использована, но при условии введения разных значений волатильности. Большинство участников рынка это и практикуют. [c.199]
Методика японских свечей может пригодиться и обладателям полностью хеджированных позиций. Допустим, вы выращиваете кукурузу, а рынок кукурузы движется в противоположном вашей наличной позиции направлении (цены на кукурузу падают). Значит, если вы хеджер-медведь, ваша фьючерсная позиция прибыльна. Допустим далее, что появилась мощная бычья модель разворота и вы уверены в подъеме цен. Тогда вам, возможно, захочется уменьшить размер фьючерсной позиции или закрыть ее. В некоторых случаях ликвидация прибыльного хеджа на раннем этапе может улучшить ваше финансовое положение. [c.274]
Как видно из рисунка 19.1, в 1988 году на рынке сои произошел мощный подъем, в результате которого цены выросли почти вдвое — с 6 до II долл. В середине 1988 года, вблизи пика этого подъема, свечи подали сигнал разворота посредством медвежьей модели поглощения. При использовании традиционных западных методов подобная конфигурация не рассматривалась бы как модель разворота на вершине. Для западной модели разворота на вершине потребовалось бы образование нового максимума с последующей ценой закрытия ниже уровня закрытия предыдущей недели. Черная же свеча в модели поглощения не дала нового максимума. Таким образом, с точки зрения западного аналитика образованная конфигурация не была моделью разворота на вершине, но являлась таковой согласно методу японских свечей. Для фермера, выращивающего сою, эта медвежья модель поглощения могла бы послужить сигналом либо открыть короткий хедж, либо — если его будущий урожай хеджирован не полностью — увеличить размер хеджа. [c.275]
Сначала мы в общих чертах коснемся развития экономической мысли в отношении обратной связи и самоорганизации. Затем опишем, как положительная обратная связь может воздействовать на цены в результате использования стратегий хеджирования производными бумагами и страхования инвестиционного портфеля. Далее мы перейдем к рассмотрению механизма положительной обратной связи в целом, известного в настоящее время как "стадный инстинкт" или "эффект толпы", и используем для этого имитационные процессы. Мы представим простую модель наилучшей стратегии инвестирования, которую инвестор может усовершенствовать в процессе общения с другими инвесторами и на основе полученной от них информации. Мы покажем, как поддержание такого общения может привести к возникновению значительного кооперативного феномена, при котором рынок [c.92]
Проблема нестабильности становится еще более острой. Вера в основные показатели исчезает, а поведение, заключающееся в следовании за доминирующей тенденцией, становится массовым. Оно формируется под растущим влиянием институциональных инвесторов, результаты деятельности которых измеряются относительными, а не абсолютными показателями, и банков - центров денежных средств, действующих в качестве участников финансового рынка, которые формируют его состояние и являются провайдерами (проводниками) механизмов хеджирования. Роль страховых фондов амбивалентна они используют леверидж, т.е. опираются на определенное соотношение заемных и собственных средств, и тем самым поддерживают непостоянство на рынке но делают они это только в той степени, в какой их поведение может быть мотивировано абсолютными, а не относительными показателями деятельности. Поэтому они часто действуют в направлении, обратном тенденции. Поскольку финансовые рынки сами развиваются согласно историческим тенденциям, нельзя относиться легко к опасности увеличения нестабильности. Я анализирую эту опасность в главах о системе мирового капитализма, но перед тем как мы подойдем к этому, нам следует подробнее познакомиться с рефлексивностью и историческими моделями. [c.46]
Чтобы воспроизвести опцион колл в условиях биноминальной модели, необходимо купить h акций [где h - коэффициент хеджирования из уравнения (20.5)]. Одновременно необходимо получить под ставку без риска средства путем короткой продажи облигации. Эта сумма равна [c.655]
Наклон кривой стоимости опциона Блэка-Шоулза в любой точке представляет собой ожидаемое изменение стоимости опциона при изменении цены базисной обыкновенной акции на 1. Данная величина соответствует коэффициенту хеджирования опциона колл и равна N(dt) в уравнении (20.10). Как видно из рис. 20.6 (предполагается, что рыночная цена опциона колл равна стоимости, полученной по модели Блэка— [c.664]
Следует отметить, что даже если модель Блэка-Шоулза верна и правильно определены все переменные, риск для хеджированного портфеля нельзя считать полностью исключенным на все оставшееся время после его формирования (или, что то же самое, на любой момент времени). Так происходит потому, что коэффициент хеджирования будет меняться при изменении цены акции и уменьшении срока действия опциона. [c.665]
Для моделей с непрерывными ценами активов методика хеджирования при [c.51]
Анализ метода квантильного хеджирования в рамках модели [c.73]
| Таблица 2 Множество успешного хеджирования в зависимости от параметров модели |  |
| Таблица 4 Моделирование процедуры совершенного хеджирования купленного опциона колл в классической модели Блэка-Шоулса | 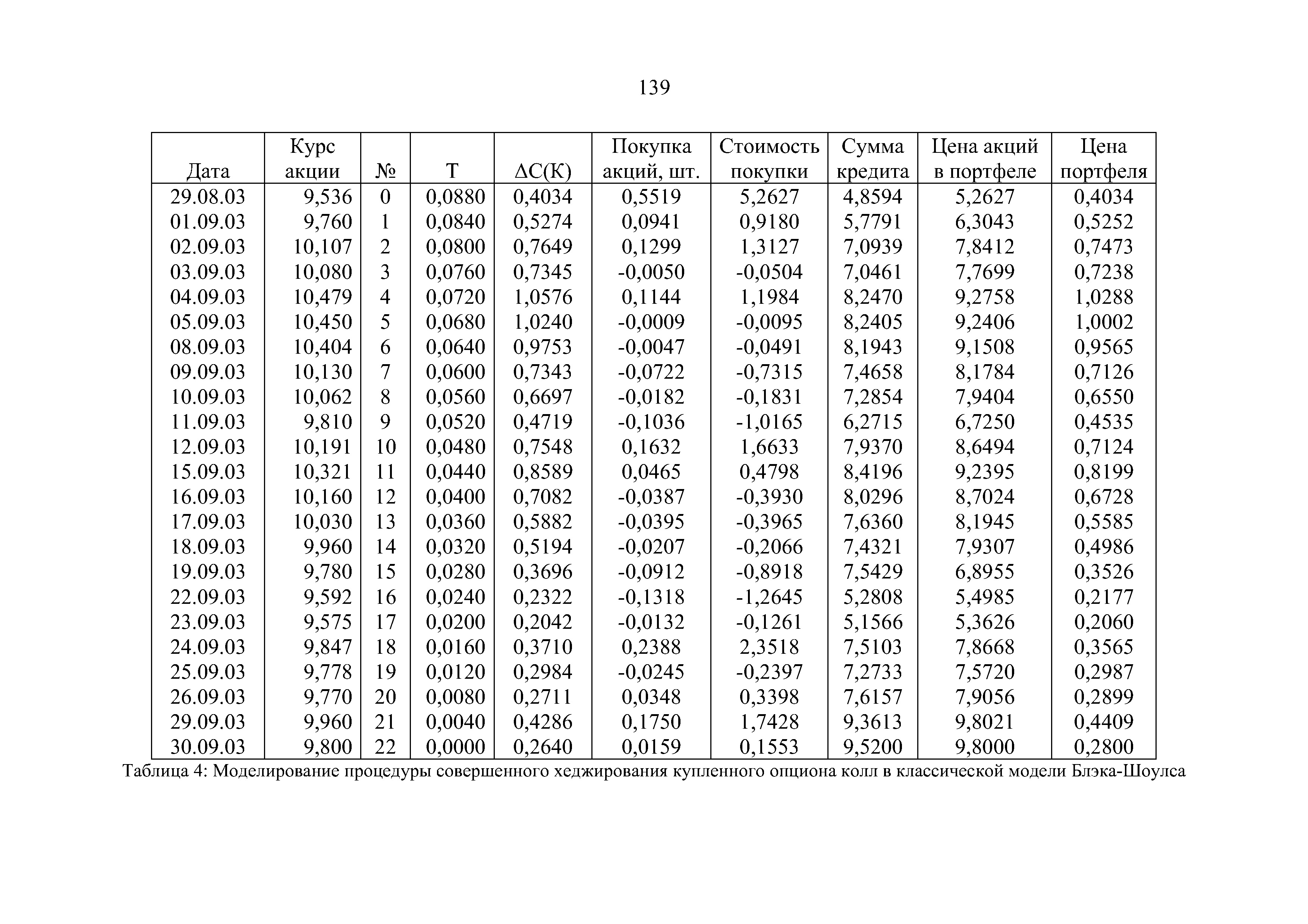 |
| Таблица 6 Моделирование процедуры хеджирования ожидаемых потерь в классической модели Блэка-Шоулса | 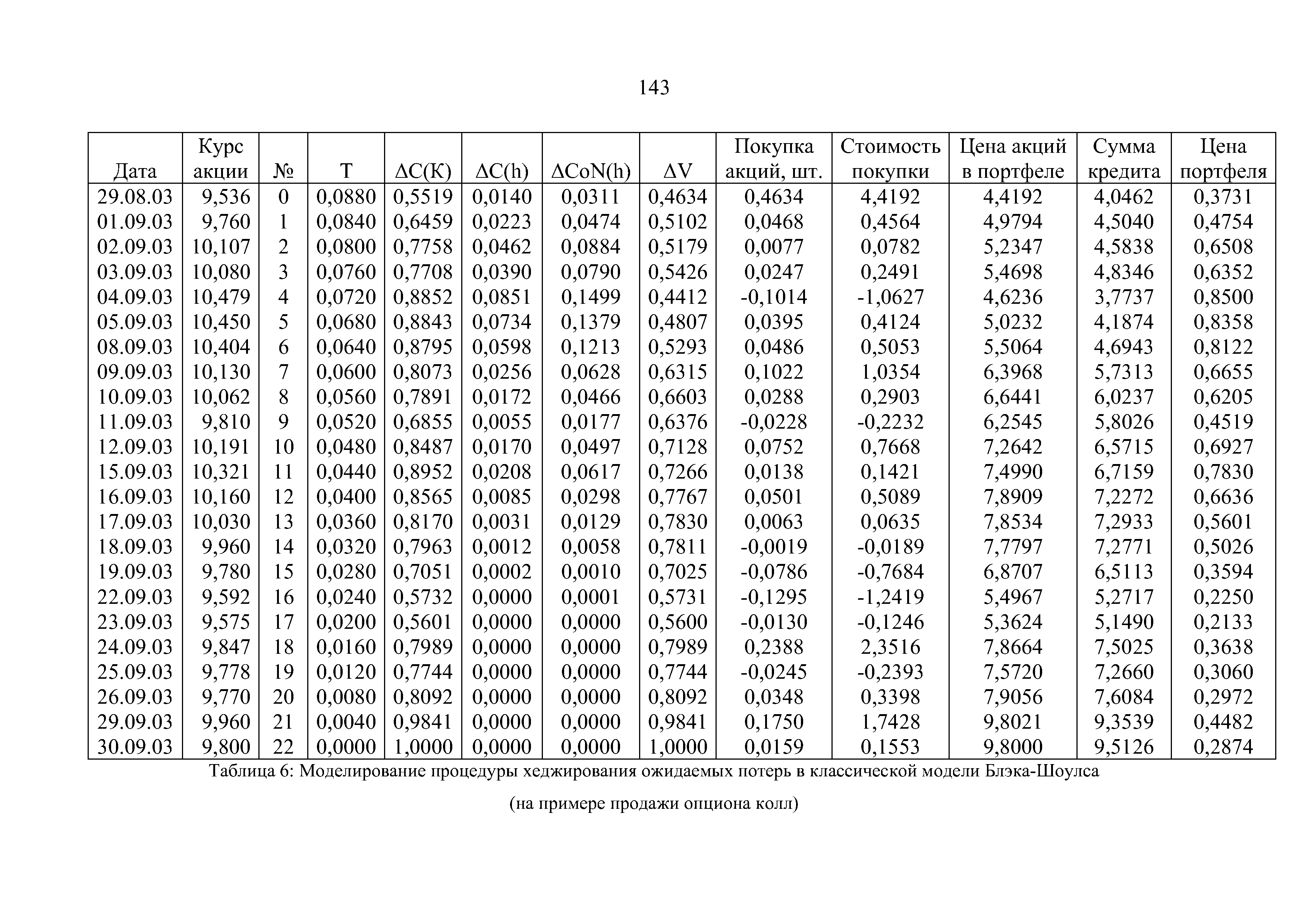 |
В конструктивной работе Фишер Блэк и Майрон Шолс разработали модель определения равновесной стоимости опциона. Эта модель основана на понятии хеджирования, которое мы только что обсуждали. Блэк и Шолс сделали следующие допущения опцион может быть использован только в срок, нет трансакцион-ных издержек или несовершенств рынка по акциям не выплачиваются дивиденды известна краткосрочная процентная ставка, по которой субъекты рынка могут и привлекать средства, и предоставлять ссуды, и наконец, колебания цен на акции происходят произвольно. [c.662]
При решении задачи по данной формуле мы находим текущую цену акции, срок до окончания действия опциона, цену использования и краткосрочную ставку процента. Неизвестная переменная в таком случае — стандартное отклонение. Его следует вычислить. Стандартный подход — использование колебания прибыли по акциям за прошедшие периоды в качестве показателя на будущее. Блэк и Шолс так же, как и другие авторы, проверили модель, используя стандартные отклонения, оцененные по прошедшим периодам с определенной степенью успеха. Оценив равенство для опционов Блэк и Шолс получили соотношение акций и опционов, необходимое для поддержания полностью хеджированной позиции. В уравнении — это N(d ). Таким образом, модель Блэка—Шолса позволяет дать количественную оценку факторам, влияющим на стоимость опциона. Как мы видим, главным фактором является определение будущих колебаний акций. [c.665]
Модель цены опциона Блэка—Шолса дает точную формулу для определения стоимости опциона, основанную на изменчивости акций, ценах акций, цене использования опциона, времени до окончания срока его действия и краткосрочной ставке процента. Модель основана на предположении о том, что инвесторы способны поддерживать относительно хеджированные позиции во времени и что арбитражные сделки приведут прибыль на этой позиции к безрисковой ставке процента. В результате цена опциона имеет четкую взаимосвязь с целой акций. Модель Блэка— Шолса позволяет уяснить себе проблемы стоимостной оценки опционов. [c.666]
В целом если два человека имеют разные вкусы, им целесообразно формировать разные инвестиционные портфели. Вы можете хеджировать ваши потребности, вкладывая капитал в виноделие, в то время как кто-то другой предпочтет инвестиции в компанию Baskin and Robbins. Однако модель оценки долгосрочных активов компании не дает объяснения таким событиям. Она исходит из предположения, что все инвесторы имеют одинаковые вкусы. "Мотив" хеджирования не учитывается, и поэтому согласно модели инвесторы держат одинаковые портфели рисковых активов. [c.1021]
Примечание. Основано на модели Блэка—Шольиа. Вычесть 1,0 для получения соответствующих коэффициентов хеджирования для европейских опционов "пут". [c.1040]
Далее следует найти, какая часть пакета акций необходима для дублирования дохода по опциону "колл". Такая часть называется коэффициентом хеджирования (Ьейле гапо) опциона. В более широком смысле коэффициент хеджирования в двухступенчатой модели представляет собой разность между двумя возможными денежными платежами по опциону, делённую на разность двух возможных предельных цен пакета подлежащих акций В данном случае это [c.272]
На практике портфельные менеджеры используют неагрессивные методы динамического хеджирования, что предполагает отсутствие торговли самими ценными бумагами портфеля. Стоимость портфеля зависит от текущей дельты и модели и регулируется с помощью фьючерсов, а иногда пут-опционов. Плюсом использования фьючерсов является низкая стоимость трансакций. Короткая продажа фьючерсов против портфеля эквивалентна продаже части портфеля. При падении портфеля продается больше фьючерсных контрактов, когда же стоимость портфеля растет, эти короткие позиции закрываются. Потери по портфелю, когда приходится закрывать короткие фьючерсные позиции при росте цен на акции, являются издержками по страхованию портфеля и эквивалентны стоимости гипотетических смоделированных опционов. Преимущество динамического хеджирования состоит в том, что оно позволяет с самого начала точно рассчитать издержки. Менеджерам, применяющим такую стратегию, это позволяет сохранить весь портфель ценных бумаг, в то время как размещение активов регулируется посредством фьючерсов и/или опционов. Предложенный неагрессивный метод, основанный на использовании фьючерсов и/или опционов, позволяет разделить размещение активов и активное управление портфелем. При страховании вы должны постоянно регулировать портфель с учетом текущей дельты, т. е. с определенной периодичностью, например, каждый день вы должны вводить в модель ценообразования опционов текущую стоимость портфеля, время до даты истечения, уровень процентной ставки и волатильность портфеля для определения дельты моделируемого пут-опциона. Если к дельте, которая может принимать значения 0 и -1 прибавить единицу, то вы получите соответствующую дельту колл-опциона, которая будет коэффициентом хеджирования, т.е. долей вашего счета, которую следует инвестировать в фонд. Допустим, коэффициент хеджирования в настоящий момент составляет 0,46. Размер фонда, которым вы управляете, эквивалентен 50 фьючерсным контрактам S P. Так как вы хотите инвестировать только 46% средств, вам надо изъять остальные 54%, т.е. 27 контрактов. Поэтому при текущей стоимости фонда, при данных уровнях процентной ставки и волатильности фонд должен иметь короткие позиции по 27 контрактам S P одновременно с длинной позицией по акциям. Так как необходимо постоянно перерассчитывать дельту и регулировать портфель, метод называется стратегией динамического хеджирования. Одна из проблем, связанная с использованием фьючерсов, состоит в том, что рынок фьючерсов в точности не следует за рынком спот. Кроме того, портфель, против которого вы продаете фьючерсы, может в точности не следовать за индексом рынка спот, лежащего в [c.234]
Как это ни странно, многие категории участников рынка, такие как, например, маркет-мэйкеры, занимающиеся покупкой и продажей варрантов и не придающие абсолютно никакого значения таким сложным моделям, очень хорошо улавливают реальные чувствительности цен варрантов и, устанавливают хеджи, используя верные эмпирические дельты (empiri al deltas). Они зарабатывают огромную прибыль, на самом деле не зная даже почему. По прошествии времени умудренные опытом хеджеры все больше и больше втягиваются в рынок и для расчета дельт предпочитают использовать эмпирический статистический анализ вместо модели Блэка-Шоулза. Конечным результатом этого хеджирования оказывается, к сожалению, исчезновение аномалий. Японские варранты теперь торгуются по ценам, очень близким к тем, что дает модель. [c.197]
Еще одним феноменом в этой области является рост волатильности цен на рынке акций, отмечаемый и анализируемый в последние годы (в качестве убедительной иллюстрации можно, к примеру, обратиться к Табл. 5), а причиной этого явления чаще всего называется популярность стратегий хеджирования с помощью производных инструментов. И действительно, исследования показывают, что оптимальные стратегии хеджирования (с использованием усовершенствованной знаменитой модели Блэка-Шоулза) не только обеспечивают положительную обратную связь с ценами, но и увеличивают волатильность цен [381]. Как отмечал Миллер (Miller) [298], в финансовой прессе практически ежедневно звучит следующее, широко распространившееся мнение рост волатильности рынка акций в последнее десятилетие происходил в основном благодаря появлению на рынке дешевых спекулятивных инструментов, таких как фьючерсы на фондовые индексы и опционы. Однако, было бы наивно объяснять рост волатильности только этой [c.99]
Данное объяснение коэффициента хеджирования следует из интерпретации формулы Блэка— Шоулза на основе модели ВОРМ, которая была представлена выше. То есть если выплаты по опциону можно воспроизвести, купив акцию и заняв средства под процент без риска, тогда покупка акции и продажа опциона колл будут аналогичны инвестированию в безрисковый актив. [c.685]
Возможно, самый известный и признанный теоретический результат в области финансов — это модель Блэка-Шоулса для определения цены опционов (ОРМ, Option Pri ing Model). Согласно этой модели, цена опциона прямо определяется предсказуемыми показателями наличного рынка соответствующих основных ценных бумаг. Поэтому очень интересно было бы выяснить, существуют ли связи типа запаздывания между ценами опционов и ценами на наличном рынке. Характерной особенностью опционов является то, что небольшие начальные вложения позволяют получать прибыль от изменения рыночных курсов, соответствующую большому количеству акций (так называемый левередж). Пантон [210] высказал мысль, что эти соображения ликвидности должны приводить к тому, что цены акций будут следовать за ценами опционов. За большинством сделок по опционам рано или поздно следуют сделки по соответствующим акциям — в частности, потому, что издатели (продавцы) опционов немедленно хеджируют свои позиции сделками на рынке акций (дельта-хеджирование), а также потому, что многие контракты исполняются раньше срока (там, где в ходу опционы американского типа). В результате та информация, на основании которой принимаются решения по сделкам с опционами, в некотором преобразованном виде передается на рынок акций. [c.114]
Смотреть страницы где упоминается термин Модель хеджирования
: [c.41] [c.45] [c.122] [c.322] [c.741] [c.260] [c.223] [c.100] [c.142] [c.6] [c.42] [c.51] [c.53] [c.73] [c.106]Смотреть главы в:
Управление финансовыми рисками -> Модель хеджирования
Экономические и финансовые риски Оценка, управление, портфель инвестиций -> Модель хеджирования
Теория риска и моделирование рисковых ситуаций -> Модель хеджирования
