Опционы с нулевой стоимостью [c.88]
Пример. Немецкий импортер хотел бы застраховать расчетную сумму в 5 млн. долл., которую он должен уплатить через некоторое время. В основу его калькуляции заложен курс USD/DEM 1,6500. На этом уровне он и намерен застраховаться от повышения курса. Хотя альтернативный форвардный курс, составляющий 1,5900, для импортера уже выгоднее, чем заложенный в калькуляции, он рассчитывает при дальнейшем снижении курса получить прибыль и решается использовать опционы с нулевой стоимостью. [c.89]
ОПЦИОН С НУЛЕВОЙ СТОИМОСТЬЮ [c.90]
| Рис. 21. Опцион с нулевой стоимостью 90 | 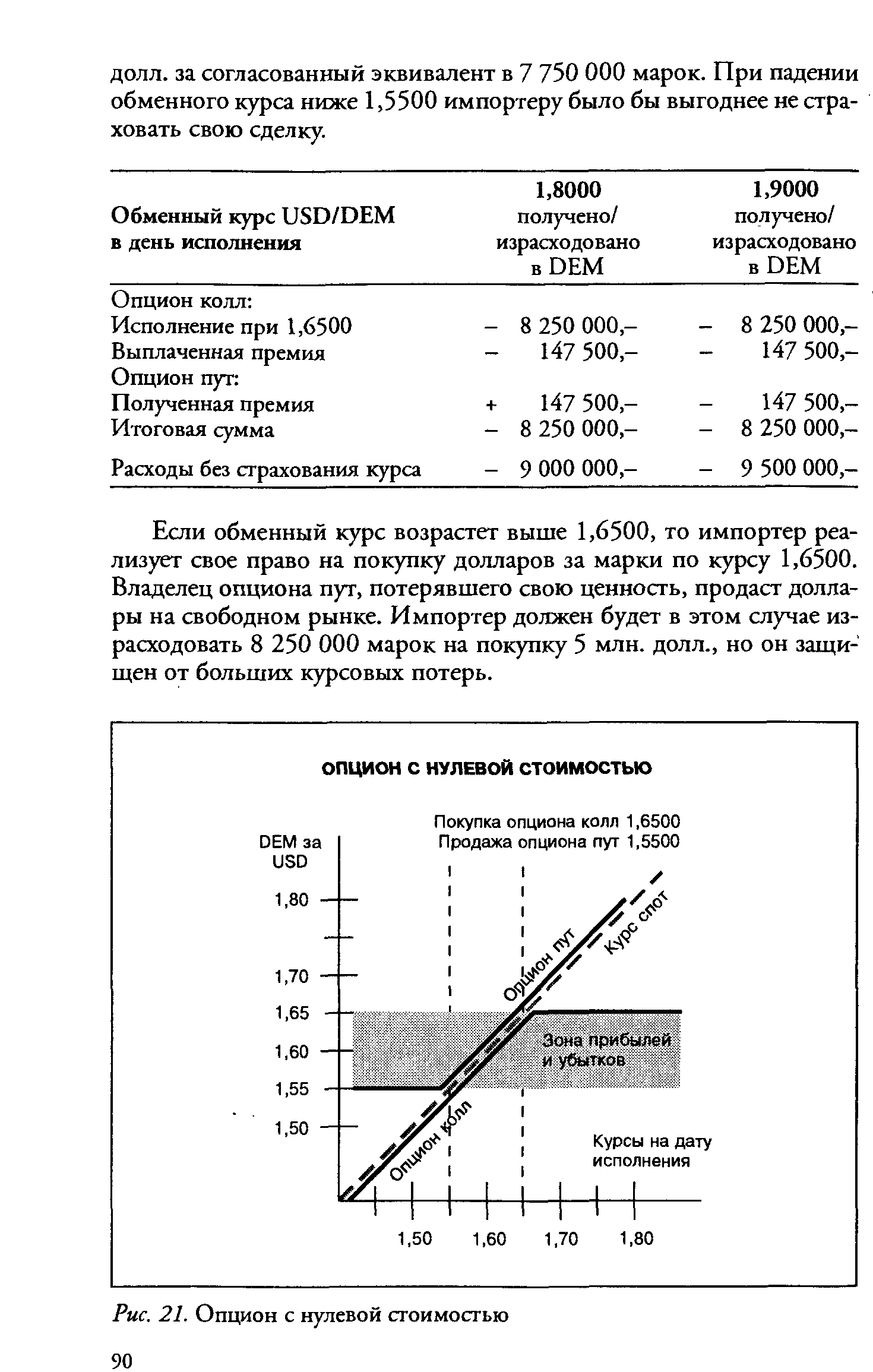 |
Ограничение прибылей и убытков посредством опциона с нулевой стоимостью по цене исполнения между 1,5500 и 1,6500 показано на рис. 21. [c.91]
В отличие от АРВ 25 Положение № 123 требует, чтобы премии в ценных бумагах оценивались не по внутренней стоимости, а по их справедливой стоимости. Метод справедливой стоимости предполагает оценку премии на дату ее предоставления и признание издержек на ее выплату на протяжении срока до момента исполнения опциона или выдачи акций. Это означает, что большинство опционов с нулевой внутренней стоимостью на дату предоставления, а следовательно, по АРВ Х- 25 не вызывающие никаких издержек у предоставившей их компании, потребуют признания таких издержек согласно Положению № 123. Поэтому практически все компании предпочитают использовать лишь те нормы Положения № 123, которые требуют раскрытия информации о методике оценки опционов в финансовой отчетности, продолжая использовать АРВ № 25 в качестве руководства по признанию издержек на их выплату. Единственным исключением остается ситуация предоставления опционов лицам, не являющимся сотрудниками компании, тогда применение всех норм Положения X 123 обязательное. [c.379]
Наш пример очень упрощен — например, мы ничего не сказали о временной стоимости денег и риске, - но он акцентирует внимание на основном моменте. Когда вы продаете варранты, вы продаете опционы и получаете в обмен денежные средства. Опционы являются ценными бумагами, имеющими стоимость. Если они оценены должным образом, это справедливая сделка — другими словами, сделка с нулевой чистой приведенной стоимостью. [c.600]
В конце 20-х годов компании и фондовые биржи создали огромное количество новых видов ценных бумаг — опционов, фьючерсов, опционных контрактов на фьючерсы облигаций с нулевым купоном, облигаций с плавающей процентной ставкой облигаций "с ошейником", "с потолком", со страховкой облигаций, деноминированных в двух валютах облигаций с валютными опционами и т. п. — этот список бесконечен. В некоторых случаях легко объяснить успех новых рынков и ценных бумаг - возможно, они позволяют инвесторам застраховаться от новых рисков, или они обусловлены изменениями в налоговом или ином законодательстве. Иногда новые рынки развиваются благодаря изменениям издержек, связанных с выпуском и обращением ценных бумаг. Но есть много успешных инноваций, которые так просто не объяснить. Действительно ли мы улучшаем свое благосостояние за счет Возможности продавать и покупать опционы на акции, а не только сами акции Почему инвестиционные банки продолжают создавать и успешно продавать новые сложные инструменты фондового рынка, определить стоимость которых порой выше наших возможностей Правда такова, что мы не понимаем, почему некоторые новшества на рынках имеют успех, а некоторые так и не находят своего покупателя. [c.1023]
Одним из лучших примеров является японский рынок варрантов периода 1987 — 1993 годов. Японские варранты являются долгосрочными опционами колл, и по разным причинам они торговались с существенным дисконтом от теоретической стоимости, которая определялась по модели Блэка-Шоулза. В то время этому расхождению придумали удобное объяснение, согласившись с тем, что модель неприменима к опционам с четырьмя или пятью годами жизни. Основные участники рынка являлись спекулянтами, которые очень редко понимали теоретические стоимости, дельты и гаммы. Они просто покупали варрант, потому что рынок шел наверх. Ликвидность этих инструментов была огромна по сравнению с той, что наблюдалась на других рынках опционов, и часто можно было купить варранты стоимостью до 20 миллионов за один день. Большой спекулятивный интерес и отсутствие всякого значительного хеджирования предполагали возникновение бесчисленных аномалий и сохранение их на целые годы. Наиболее заметное неверное оценивание возникало тогда, когда варранты шли в деньгах. Спекулянты покупали варранты, очень далеко вне денег, по любой цене, тем самым поднимая подразумеваемую волатильность до 40%. Если им везло, а в конце 80-х им везло часто, цена основного инструмента росла, увеличивая цену варранта зачастую в пять или шесть раз от первоначальной стоимости. Обрадованные такими большими компенсациями за риск, спекулянты распродавали их частями, часто толкая цену от равноценных скидок к большим скидкам от теоретических стоимостей. Цены таких варрантов в деньгах были часто ниже тех цен, которые были получены на основе моделей, использовавших нулевое значение волатильности. Эти инструменты давали возможность хеджерам создавать длинные по волатильности портфели по отрицательной стоимости, а это означало, что даже в самом худшем случае при возникновении нулевой волатильности в результате все равно будет прибыль. И все это происходило, когда японский рынок ценных бумаг переживал один из самых волатильных периодов в своей истории. [c.196]
Проблема покупки низкой волатильности связана с тем, что волатиль-ность может стать еще ниже, а продажи высокой волатильности с тем, что волатильность может стать еще выше. До тех пор, пока низкая волатиль-ность является предельно низкой волатильностью (или, как в случае с японскими варрантами, нулевой волатильностью), а высокая волатильность является предельно возможной высокой волатильностью, нет никакой гарантии возникновения прибыли. Бывают случаи, когда можно одновременно покупать низкую волатильность и продавать высокую волатильность на один и тот же инструмент. В таких ситуациях, какова бы ни была действительная волатильность, в результате будет прибыль. Рассмотрим следующий крайний случай. Определенная акция торгуется по 100. Имеются два одногодичных опциона колл с ценами исполнения 100 и 110, оцененные по 5,98 и 5,04 соответственно. Эти цены подразумевают волатильность 15% и 22% соответственно. Явно, здесь что-то не так. Оба опциона исполнимы на одну и ту же базовую акцию, поэтому должны подразумевать одну и ту же волатильность. Если бы такая ситуация на самом деле имела место, торговец составил бы портфель из длинной позиции на (уцененный) опцион с ценой страйк 100 и короткой позиции на (переоцененный) опцион с ценой страйк 110, пытаясь извлечь выгоду из разницы между двумя ценами. Портфель стал бы вертикальным колл спрэдом, или комбинацией №1, рассмотренной в седьмой главе. Комбинация имеет длинную экспозицию и доступна для хеджирования короткими акциями. Логическое обоснование этой стратегии в том, что какова бы ни была реальная волатильность акции, покупка на 15% и продажа на 22% приведет к прибыли от перепродажи по более высокой цене. Эта прибыль может быть получена одним из двух способов. Первый способ — это когда рынок внезапно устанавливает цены опционов таким образом, чтобы оба они имеют одинаковую (новую) подразумеваемую волатильность. Например, если рынок определил, что оба опциона имеют подразумеваемые волатильности 20%, то их цены будут равны 7,97 и 4,29 соответственно, в результате чего прибыль составит 100 х (7,97 — 5,98 + 5,04 — 4,29) = 274. Другим способом может быть такой, когда позиция приходит к истечению срока после продолжительного динамического хеджирования. Какова бы ни была окончательная волатильность, прибыль (теоретически) должна быть и чаще всего бывает одинаковой, но из-за того, что стоимость хеджирования не является нулевой, конечная прибыль обычно бывает маленькой. Однако даже в такой ситуации [c.198]
Допустим, что вы оцениваете собственный капитал фирмы, активы которой в настоящее время оцениваются в размере 100 млн. долл., а стандартное отклонение ценности этих активов составляет 40%. Номинальная стоимость долга составляет 80 млн. долл. (речь идет о долге с нулевым купоном и оставшимся сроком до погашения 10 лет). Ставка по казначейским облигациям с 10-летним сроком составляет 10%. Мы можем оценить собственный капитал как колл-опцион фирмы, используя следующие исходные данные для модели оценки опциона [c.1093]
Ценность базового актива = S = ценность фирмы = 100 млн. долл. Цена исполнения = К = номинальная стоимость долга = 80 млн. долл. Срок опциона = t = срок долга с нулевым купоном = 10 лет Дисперсия ценности базового актива = ст2 = дисперсия ценности фирмы = 0,16 Безрисковая ставка процента = г = ставка по казначейским облигациям, соответствующим сроку опциона = 10%. [c.1093]
Каждое из этих допущений имеет определенные причины. Во-первых, ограничение требований только долгом и акциями делает проблему легче разрешимой. Введение других требований, таких как привилегированные акции, делает получение какого-либо результата более трудным, хотя и не невозможным. Во-вторых, допуская только один выпуск долга с нулевым купоном, который может быть выкуплен по номинальной стоимости в любое время до наступления срока платежа, мы более тесно связываем характеристики долга с характеристиками цены исполнения стандартного опциона. В-третьих, если долг имеет купон, или существует более одной эмиссии долга, то возможно, что у инвесторов в собственный капитал возникнет побуждение исполнить опцион (ликвидировать фирму) в момент выплаты купонов, если они не наблюдают денежных потоков, необходимых для выполнения долговых обязательств. [c.1098]
Аппроксимация заключается в использовании в модели оценки опциона взвешенной по номинальной стоимости продолжительности облигаций с нулевым купоном. [c.1100]
Инвестирование в рискованные проекты. Поскольку собственный капитал представляет собой опцион колл на ценность фирмы, то, при прочих равных условиях, увеличение дисперсии ценности фирмы будет способствовать росту ценности собственного капитала. Поэтому акционеры могут инвестировать в рискованные проекты с отрицательной чистой приведенной ценностью, которые, хотя и улучшают их положение, могут сделать облигации и фирму менее ценными. Для того чтобы разобраться с этим, рассмотрим фирму, о которой говорилось в иллюстрации ЗОЛ, с ценностью активов, равной 100 млн. долл., номинальной стоимостью долга с нулевым купоном, выпущенного на 10 лет, в размере 80 млн. долл. Стандартное отклонение ценности фирмы составляет 40% (оценка из предыдущей иллюстрации). Собственный капитал и долг этой фирмы оцениваются следующим образом [c.1104]
Наша формула показывает, как следовало бы оценивать варранты, но на свободном рынке они редко оцениваются именно таким образом вместо этого рыночный курс варранта неизменно превышает его расчетную (или истинную) стоимость. Это происходит тогда, когда варранты с отрицательной стоимостью продаются по курсам, превышающим нулевую отметку, а также когда варранты с положительным значением стоимости продаются по еще более высоким рыночным курсам (например, когда варрант, оцененный в 10 долл., продается за 15 долл.). Такое расхождение известно как премия на варрант и имеет место постольку, поскольку варранты обладают спекулятивной ценностью. Как правило, размер премии, зафиксированный в рыночном курсе варранта, прямо зависит от срока истечения этого опциона и от колебаний курсов лежащих в его основе обыкновенных акций, т.е. чем дольше срок действия варранта и чем более неустойчивы курсы акций, тем выше размер премии. Однако размер премии имеет тенденцию к уменьшению по мере того, как стоимость варранта увеличивается. Это можно увидеть на рис. 11.2, который иллюстрирует типичную динамику премий на варранты. Премию легко определить достаточно взять разницу между стоимостью варранта (рассчитанную по приведенной выше формуле) и его рыночным курсом. Например, премия на варрант составляет 5 долл., если он имеет стоимость 10 долл., а продается за 15 долл. Мы также можем перевести сумму премии в процентное выражение, разделив эту сумму в долларах на истинную (расчетную) стоимость варранта. В нашем примере премия на 15-долларовый варрант составляет 50% (5 долл. 10 долл. = 0,5). Премии на варранты могут иногда быть значительными на практике премии в 20—30% и более не столь необычны. [c.540]
В таблице 15.2 С = 0.1, а Xo/F = 1.0. Поскольку Хо - цена исполнения, а F -форвардная цена, опцион имеет нулевую внутреннюю стоимость, аир могут изменяться. Уменьшение а приводит к повышению цены опциона, поскольку устойчивые распределения имеют более высокий пик в среднем, и, следовательно, более вероятно, что они, а не нормальное распределение, будут иметь нулевую внутреннюю стоимость. Когда a = 2.0, бета не оказывает никакого влияния. Однако для других значений беты цена повышается вместе с асимметрией. [c.221]
Чем меньше случайные колебания стоимости портфеля, тем совершеннее хедж. Сам факт случайных колебаний стоимости портфеля объясняется тем, что реальный хедж осуществляется дискретно как по времени, так и по А, к тому же волатильность цены базисного актива не является постоянной. Чем меньше дискретность, тем стабильнее стоимость портфеля, и в пределе непрерывной коррекции она является постоянной - нулевой. Дискретность проявляется тем сильнее, чем ближе дата экспирации опционов, поскольку для опционов вблизи денег коэффициенты Г и 0 возрастают по мере приближения даты экспирации. Особенно наглядно это проявляется 29.05.02, когда в результате резкого падения цены вариационная маржа оказывается в районе 40 рублей на один опцион. С другой стороны, если бы колебания цены были бы меньше прогнозируемых, то портфель столь же быстро терял бы стоимость. [c.55]
Если в конце периода ТР < X, то держатель исполнит опцион, и портфель А будет стоить X. Если Р > X, то опцион не исполнится и стоимость портфеля равна Р. Таким образом, в момент Т портфель А стоит или Р или X. Облигация с нулевым купоном в конце периода гасится по номиналу, который равен X, и портфель Б стоит X. Поэтому портфель А будет всегда стоить столько же или больше, чем портфель Б (см. таблицу 23). [c.136]
На следующий день фьючерсная котировка падает до 4765, цена опциона колл уменьшается до 150, а опциона пут возрастает до 370. Опционная волатильность комбинации равна 35.4%. График позиции показан на рис. 20. Сечение кривой стоимости на текущей фьючерсной цене равно 8175 и показывает прибыль которая образуется при закрытии фьючерсных и опционных позиций (без учета спрэдов и комиссионных). Если трейдер намерен удерживать позицию, то необходимо учесть, что дельта позиции равна —30.45. В случае ожидания дальнейшего падения фьючерсной цены можно оставить позицию с имеющимся наклоном, однако если такой уверенности нет, то лучше ликвидировать образовавшийся наклон покупкой 30 фьючерсов по цене 4765. Результат коррекции изображен на рис. 21. Позиция с нулевой дельтой называется дельта-нейтральной, а ее поддержание обеспечивается регулярными фьючерсными коррекциями — динамическим хеджем. [c.429]
Части рис. 20.4 (б) и (г) представляют собой зеркальное отражение частей (а) и (в). Опционы — это игра с нулевой суммой, где выигрыши одной стороны возникают за счет другой, поэтому, если цена акции равна 108, то покупатель опциона колл получит выигрыш в 3, а продавец опциона колл будет иметь проигрыш в 3 (продавец получает премию в 5 и 100 в качестве цены исполнения, но должен поставить акцию стоимостью в 108). Аналогично, если покупатель опциона пут выигрывает 3, то продавец опциона пут проигрывает 3. [c.650]
Если существует некая вероятность положительного дохода и если наихудшим результатом может быть нулевой доход, то опцион должен обладать ценностью. Это означает, что цена опциона в точке С превышает его значение на нижней пограничной линии, которое в точке С равно нулю. В целом до истечения срока опциона цены опционов превышают их минимальные стоимости (значения которых представлены нижней пограничной линией). [c.541]
Возможность инвестировать в завод по производству маринованной селедки равнозначна опциону "колл". В случае, если инвестиции осуществляются сейчас или никогда, значения стоимости опциона "колл" представлены красной сплошной линией. Если осуществление инвестиций можно отложить, опцион "колл" будет иметь стоимость даже при нулевой или отрицательной чистой приведенной стоимости проекта. Сравните с рисунком 20-8. [c.569]
Обратите внимание на значительное сходство двух ценовых кривых. Обе они приближаются к горизонтальной линии (нулевой цене) и обе сближаются с линией внутренней стоимости. Кривые немного отличаются в экстремумах. Кривая Блэка-Шоулза (т.е. логнормальная) выводится из сложной системы уравнений, в то время как "наивная" кривая является результатом совсем несложной арифметики. Обе кривые демонстрируют асимметричность ценовых профилей к дате истечения, а возникшее расхождение можно рассматривать как вероятности различных исходов. Целью этой главы было доказать с помощью простых аргументов, что причины, лежащие в основе наблюдаемой нелинейности цен опционов, не зависят от используемого способа доказательства. Нет необходимости детально разбираться в поведении кривой ценового профиля. Скорее, нужно понять, почему эта кривая существует вообще. [c.51]
Простейший случай — когда цена акции остается совершенно неизменной до истечения срока. С приближением срока истечения условия хеджирования будут изменяться, но все сделки будут происходить при неизменной цене акции, а при истечении срока хеджирование акции будет полностью раскручиваться при одной и той же цене акции. В этой ситуации убыток стратегии становится равным временной стоимости самого опциона. Рисунок 4.16 показывает убытки (тип 1), наблюдаемые при таком типе нулевой волатильности. [c.99]
Начиная с опционов колл, процедура осуществляется следующим образом. Если все опционы торгуются по внутренней стоимости, то длинные позиции на опционы колл будут иметь экспозицию +100 акций над ценой страйк и нулевую экспозицию ниже цены страйк. Короткие позиции по опционам колл будут иметь экспозицию -100 акций над ценой страйк и нулевую экспозицию ниже цены страйк. В качестве примера рассмотрим портфель, состоящий из опционов колл. Все его характеристики приведены в таблицах на Рисунке 7.11. Для них используется обычное обозначение "+" отражает длинную позицию, а "—" короткую. Обратите внимание на две противоположные экспозиции акции каждого опциона по обе стороны каждой цены страйк. [c.179]
В другом случае финансовый директор мог бы обратиться к банкам с целью приобретения внебиржевого опциона с нулевой стоимостью (иногда называемого "цилиндр" или коллар). Возможно, стоило бы купить предложенные банками опционы с ценами исполнения от 1,4050 до 1,5000 долл. с нулевой чистой премией, чтобы покрыть риск, предпочтя их опционам, продаваемым на бирже. [c.160]
Предприятия являются в основном покупателями опционов, банки выступают в качестве и покупателей, и продавцов. Многие предприятия, рассматривающие покупку опциона как альтернативу форвардной валютной сделке, сталкиваются с дополнительной проблемой величиной предварительно выплачиваемой премии. Предприятие — покупатель опциона хочет покрыть свои валютные риски, использовать благоприятное для него изменение курсов и одно-времена уплатить возможно меньшую премию или даже не платить ее совсем. Покупка опциона в комбинации с продажей имеет наименование опционы с нулевой стоимостью (zero- ost options). [c.88]
На практике редко удается выравнять уплаченную и полученную премии, но премиальные расходы можно снизить до минимума. Принцип использования опционов с нулевой стоимостью рассматривается далее на примере при этом премии при покупке и продаже для упрощения представлены равными. [c.89]
ВНУТРЕННЯЯ СТОИМОСТЬ ОПЦИОНА (intrinsi value) — разница между рыночной стоимостью ценной бумаги при продаже опциона и ценой использования опциона. Опционом с положительной внутренней стоимостью он называется, если цена его использования более выгодна, чем текущая стоимость ценных бумаг. Если текущая стоимость и цена использования равны, то это опцион с нулевой внутренней стоимостью. При цене использования ниже текущей стоимости ценных бумаг опцион будет с отрицательной внутренней стоимостью. [c.57]
Нет ничего более запутанного, чем конвертируемые отзывные облигации с нулевым купоном и правом досрочной продажи. В августе 1989 г. фирма hemi al Waste Management выпустила такие облигации по цене 30,7% с нулевым купоном и со сроком погашения 20 лет, конвертируемые в фиксированное количество акций в любое время, хотя компания имела возможность вместо этого выплатить эквивалент стоимости акций в денежной форме. В дополнение к этому облигационеры обладали опционом на продажу облигаций самой компании за [c.664]
Предыдущий пример содержит и другие уроки. Все показанные опционы пут находятся без-денсг, поскольку их цена исполнения 1900 значительно ниже цен базовых фьючерсов. Следовательно, их внутренняя стоимость равна нулю. Когда опцион имеет нулевую внутреннюю стоимость, его премия целиком состоит из временной стоимости. Это означает если ничего больше не изменится, то н с и ос ре летне н но перед истечением опциона премия снизится практически до нуля. Именно поэтому иногда опцион называют "никчемным актином" (wasting asset). Примером служит пут по июньской сырой нефти 1900. Этот опцион без-денег находится очень близко от срока истечения, и его премия (полностью состоящая из временной стоимости) равна только 0,01 х 1000 баррелей S10. [c.151]
Оцените, с запасом, насколько должны измениться цены, чтобы развернуть тренд. Продавайте опционы по ценам за пределами этого диапазона. Продавайте опционы с такими ценами исполнения, которые вряд ли будут достигнуты в период действия опциона. Предположим, акции продаются по 80, при этом их цены за последний год выросли с 50 и теперь повышаются на полпункта в неделю, а до истечения опциона остается восемь недель. Тренд растет, и в этих условиях, продавая опцион пут с ценой исполнения 70, мы продаем опцион, который к моменту истечения срока, скорее всего, будет иметь нулевую стоимость. [c.220]
Опционы с ускоренным исполнением позволяют избежать проблем с финансовым учетом, характерных для предыдущего варианта. Обычно они выпускаются с нулевой внутренней стоимостью на срок, превышающий тот, который отводится для оценки результатов деятельности, например на семь лет. Если плановые задания успешно реали зуются, то срок исполнения опциона пересматривается в сторону уменьшения. Если же плановые задания не выполняются, то житейская мудрость подсказывает, что вряд ли топ-менеджеры захотят так долго задерживаться на своих постах. [c.221]
Рассмотрим ситуацию за день до экспирации, когда возможными значениями котировки являются 4800, 5000, 5200, 5400, 5600. Если котировка равна 4800, то при любом из двух сценариев следующего дня сумма, полученная по опциону, будет равна 0, поэтому и в узле 4800 необходимо поставить нулевую стоимость опциона. Более интересен узел 5000. Предположим, что в этой ситуации, то есть за день до экспирации и при сложившейся к этому моменту фьючерсной котировке 5000, куплено М опционов. Если котировка фьючерса уменьшится до 4900, то держатель опционов получит 0, а если котировка возрастет до 5100, то полученная сумма окажется равна 100 по каждой открытой позиции. Имеется способ устранить эту неоднозначность, продав одновременно с покупкой опционов фьючерсные контракты в количестве А—0.5М. Тогда, как нетрудно проверить, независимо от сценария следующего дня сумма, полученная держателем опционов, будет равна 50М. Действительно, при падении котировки до 4900 по коротким фьючерсным позициям будет получено 100Л, а при росте котировки по опционам будет получено 100М, но одновременно потеряно 100Л по фьючерсам. При указанном выше выборе коэффициента А оба исхода приводят к одинаковому результату 50М. Это означает, что стоимость одного опциона составляет 50. Комбинация, состоящая из купленных М опционов и проданных А фьючерсов, или противоположная ей - проданные М опционов и купленные А фьючерсов - являются частными случаями так называемого безрискового или дельта-нейтрального портфеля. [c.36]
Приблизительно нулевая вариационная маржа по портфелю в таблице 9.3 означает, что вариационная маржа по фьючерсным позициям достаточно точно воспроизводит уменьшение или увеличение стоимости 100 проданных опционов. Из этого следует, что покупку или продажу опционов можно имитировать, постоянно поддерживая открытую фьючерсную позицию равной А опционов. Эта процедура называется воспроизведением опционов (option repli ation te hnique). Динамический хедж в рассмотренном выше примере по существу представляет собой единовременную покупку настоящих опционов и имитацию продажи тех же опционов с помощью фьючерсов. [c.58]
Ответим теперь на поставленный выше вопрос, но применительно к американскому опциону пут. Сравним два портфеля. Портфель А состоит из одного американского опциона пут и одной акции. В портфель Б входит одна облигация с нулевым купоном стоимостью ХегТ. При досрочном исполнении опциона (время t) портфель А будет стоить X, портфель Б — Хёг(Т 1). Если инвестор держит опцион до момента истечения контракта, то в зависимости от цены енот акций портфель А будет равен X или Р. Портфель Б в этот момент равен X. Таким образом, в случае раннего исполнения опциона портфель А больше портфеля Б. Если опцион держится до момента истечения контракта, то портфель А равен или больше портфеля Б. Изложенные рассуждения представлены в таблице 25. [c.138]
Чтобы определить нижнюю границу премии европейского опциона колл, рассмотрим два портфеля — А и Б. Портфель А состоит из одной акции. Портфель Б — из европейского опциона колл, облигации с нулевым купоном, равной ХегТ и суммы денег, равной D (D — это приведенная стоимость дивиденда, который выплачивается по акциям. Она получена путем дисконтирования дивиденда под непрерывно начисляемую ставку без риска г на время Т. Составляя часть портфеля Б, сумма D инвестируется на время Т под процент г). [c.140]
Предположим, имеется два портфеля — А и Б. Портфель А состоит из одного европейского опциона колл и облигации с нулевым купоном, равной ХегТ. В портфель Б входит один европейский опцион пут и одна акция. Если к моменту истечения контракта Р > X, то портфель А равен Р и портфель Б также равен Р. Если Р < X, то портфели А и Б равны X. Таким образом, в конце периода Т оба портфеля имеют одинаковую стоимость. Поэтому можно сделать вывод, что в начале периода Т стоимость их также должна быть равна, то есть [c.148]
Рассмотрим два портфеля. Портфель А состоит из одною европейского опциона колл, облигации с нулевым купоном X ег и суммы денег D. В портфель Б входят один европейский опцион пут и одна акция. В конце периода Т стоимость портфелей будет равна (см. табл. 29). [c.151]
Смотреть страницы где упоминается термин Опционы с нулевой стоимостью
: [c.147] [c.217] [c.204] [c.143] [c.81]Смотреть главы в:
Валютные операции основы теории и практики -> Опционы с нулевой стоимостью
