Статистическая функция распределения случайной величины всегда есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны эмпирическим вероятностям этих значений. Сумма всех скачков функции F (x) равна единице. По мере увеличения объема выборки и уменьшения интервалов Ах число скачков становится больше, а сами скачки - меньше ступенчатая кривая становится более плавной случайная величина постепенно приближается к непрерывной величине, а ее статистическая функция распределения - к непрерывной функции - интегральной функции распределения F(x). [c.24]
Поэтому возникает необходимость такого задания функции распределения, которое подходило бы для непрерывных и дискретных случайных величин. С этой целью удобно иметь дело с вероятностью события Х<х, а не Х=х, как это имело место в законе распределения дискретных случайных величин. [c.18]
Используется для проверки гипотезы о функции распределения случайной одномерной непрерывной величины . [c.27]
Непрерывная случайная величина может принимать все возможные значения и задаваться в виде функции плотности вероятности. Одним из наиболее простых примеров служит величина, равномерно распределенная по некоторому интервалу, т.е. принимающая все значения из этого интервала с равной вероятностью и не принимающая значений вне этого интервала. [c.262]
Плотностью вероятности (плотностью распределения или просто плотностью) ф(х) непрерывной случайной величины X называется производная ее функции распределения [c.30]
A5/S (см. также следующий раздел). Эту характеристику по /-му ресурсу можно задавать величиной Е] — математического ожидания недопоставки АР/Р°. В случае непрерывной функции эластичности ф/ при известной плотности распределения (k.S ISj) случайной величины A5 75j она выражается так [c.29]
Для непрерывной случайной величины функция распределения F(x) носит непрерывный характер (в). [c.128]
Для непрерывных случайных величин, которые имеют непрерывную и дифференцируемую функцию распределения F(x), вводится понятие плотности распределения, которая, по существу, является производной от функции распределения [c.129]
Наиболее простым законом распределения случайных величин является закон равномерной плотности непрерывной величины, согласно которому все значения случайной величины в пределах определенного интервала одинаково вероятны. Функция распределения этой величины представлена на рис. 33, где С — некоторая постоянная величина. [c.133]
Основным признаком непрерывной случайной величины является то, что вероятность любого частного значения этой величины равна нулю. Это нетрудно доказать, воспользовавшись первым свойством функций распределения. [c.49]
Из курса теории вероятностей и математической статистики известно, что нормально распределенная случайная величина является непрерывной и ее дифференциальная функция распределения имеет вид [c.47]
Для характеристики непрерывной случайной величины определяют вероятность появления значения случайной величины меньшего х, где х - текущая переменная, т. е. определяют вероятность события X < х. Вероятность этого события зависит от х, т. е. является функцией х. Эта функция называется функцией распределения случайной величины X и обозначается F(x) [c.11]
Непрерывная случайная величина X принимает значения от -со до +оо. Соответствующая функция распределения равна [c.28]
Отсюда находим, что искомая вероятность попадания непрерывной случайной величины в интервал xt < X < х, равна разности функций распределения этой случайной величины [c.272]
ЕЗ) если X — непрерывная случайная величина с плотностью распределения р(х), а д(х), х б R — числовая функция, то для случайной величины Y = д(Х) справедливо равенство [c.511]
Функция и плотность распределения вероятности. 206 11.32 Числовые характеристики непрерывных случайных величин. 207 [c.7]
Нормально распределенная случайная величина является непрерывной и ее дифференциальная функция распределения имеет вид [c.10]
Идея вероятностного анализа долговых обязательств, представленная здесь, состоит в том, чтобы отслоить от истории сделок с долговыми обязательствами неслучайную составляющую цены (тренд). Тогда оставшаяся случайная составляющая (шум) цены может рассматриваться нами как случайный процесс с непрерывным временем, в сечении которого лежит нормально распределенная случайная величина с нулевым средним значением и со среднеквадратичным отклонением (СКО), равным a(t), где t - время наблюдения случайного процесса. Ожидаемый вид функции a(t) будет исследован нами позже. [c.84]
Для непрерывной случайной величины ее функция распределения непрерывна. [c.296]
Случайная величина X называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек. [c.30]
Дх), является одной из форм закона распределения, но в отличие от функции распределения она существует только для непрерывных случайных величин. [c.31]
Функция распределения непрерывной случайной величины (см. рис. 2.3) может быть выражена через плотность вероятности по формуле [c.31]
Плотностью вероятности (плотностью распределения или совместной плотностью) непрерывной двумерной случайной величины (X,Y) называется вторая смешанная частная производная ее функции распределения, т.е. [c.37]
Функция распределения непрерывной случайной величины имеет вид [c.19]
Для случайной величины с непрерывной и дифференцируемой функцией распределения вероятностей F(x) можно найти дифференциальный закон распределения вероятностей., выражаемый как производная F(x), то есть р(х) = dF(x)/dx. Эта зависимость называется плотностью распределения вероятностей. Плотность распределения р(х) обладает следующими свойствами [c.15]
Полученное эмпирическое распределение будет аппроксимировано непрерывной аналитической функцией, то есть будет идентифицирован закон распределения случайной величины. Также рассмотрено использование критериев согласия при идентификации закона распределения. [c.79]
Двухэтапную задачу, в которой все случайные компоненты вектора Ь(и) имеют непрерывную функцию распределения, можно приближенно свести к задаче квадратичного программирования. Для этого достаточно заменить случайные величины взвешенными суммами равномерно распределенных случайных величин [c.179]
В дискретные моменты времени п— 1, 2,. .. наблюдаются значения y(Xn)=f(xn)+v>n. Предполагается, что а — случайная величина с нулевым математическим ожиданием и что ее значения для различных моментов времени независимы и одинаково распределены с функцией распределения, обладающей непрерывной ограниченной плотностью. [c.370]
Гистограммы чаще всего применяются для изображения вариационных рядов с непрерывными значениями случайной величины X. При уменьшении величины каждого интервала гистограмма будет приближаться к некоторой плавной кривой, соответствующей графику функции плотности распределения случайной величины X. Следовательно, в результате построения гистограммы можно получить представление о дифференциальном законе распределения случайной величины X. [c.20]
Более строго, если случайная величина является непрерывной, т.е. принимает любые значения из некоторого интервала, то для нее уже нельзя определить вероятность того, что она принимает некоторое конкретное значение (точечную вероятность). Поскольку в любом конечном интервале содержится бесконечное число значений, то вероятность выпадения одного из них всегда равна нулю. Однако функция распределения случайной величины F x), определяемая как вероятность того, что случайная величина принимает значение меньше данного числа х. [c.259]
В последних двух равенствах мы использовали определение бесконечно малого изменения функции распределения (или дифференциала этой функции). Из найденного соотношения видно, что вероятность попадания непрерывной случайной величины в бесконечно малый интервал х<Х< х + dx бесконечна мала и пропорциональна величине этого интервала dx. Отношение этой бесконечно малой вероятности к бесконечно малой величине интервала имеет конечное значение и характеризует плотность вероятности в точке х. [c.273]
Можно выделить два класса случайных величин — дискретные и непрерывные. Случайная величина X называется дискретной, если множество ее значений конечно или счетно. Несмотря на то что функция распределения универсальным образом описывает вероятностный характер случайной величины, дискретную случайную величину удобно представлять в виде таблицы [c.510]
Случайная величина X называется непрерывной, если ее функция распределения дифференцируема, т. е. существует производная р(х) = F (x), называемая плотностью распределения случайной величины X. В этом случае для любого (измеримого) множества A R справедливо равенство [c.510]
Случайные величины. Функция распределения и ее свойства. Дискретные и абсолютно непрерывные распределения случайных величин. Ряд и плотность распределения, их свойства. Примеры распределений. Нормальное распределение. [c.30]
Многомерные случайные величины (вектора), функция распределения случайного вектора. Дискретные и абсолютно непрерывные многомерные распределения. [c.30]
| Рис. 11.1. График функции распределения непрерывной случайной величины | 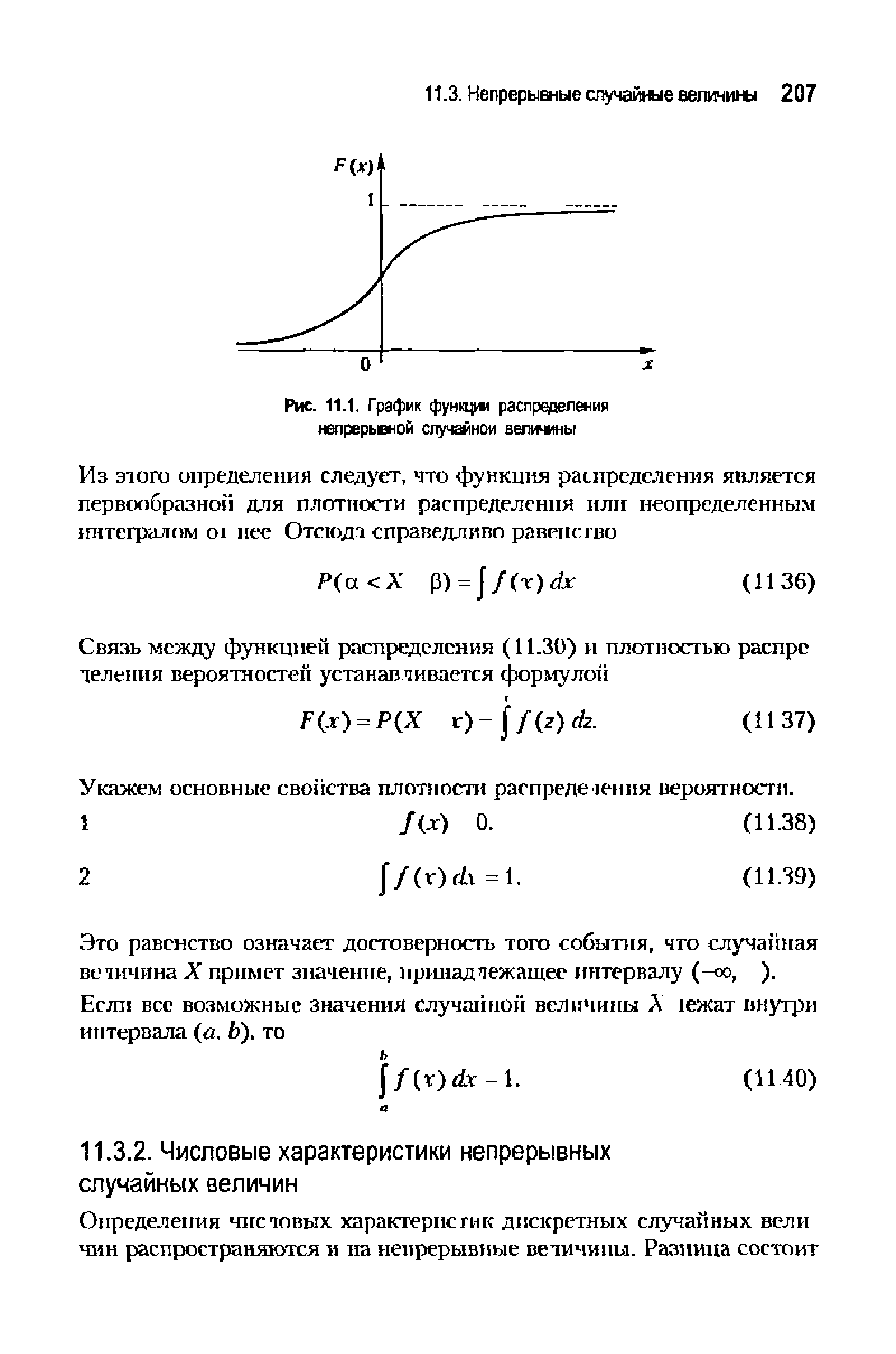 |
Поток событий однородные события неоднородные события регулярный поток событий поток без последействия ординарный поток пуассоновский поток стационарный поток пуассоновский стационарный (простейший) поток интенсивность (средняя плотность) потока потоки, сравнимые по интенсивности дискретная случайная величина Х(т), представляющая собой число событий, наступающих за временной промежуток т элемент вероятности наступления события непрерывная случайная величина Т, представляющая собой промежуток времени между двумя любыми соседними событиями потока показательный (экспоненциальный) закон распределения интегральная функция распределения дифференциальная функция распределения. [c.86]
Рассмотрим случайную величину T(t0) — промежуток времени между двумя соседними событиями в потоке, первое из которых наступило в момент времени t0. Эта непрерывная случайная величина будет распределена уже не по показательному закону как величина Т (см. Определение 5.12 и формулу (5.14)) вид ее закона распределения будет зависеть от Г0 и от вида функции / ( ) Формулы характеристик случайной величины T(t0), полученные на основе их стандартных определений аналогично тому, как это делалось в доказательстве теоремы 5.3, собраны в таблице 6.2. [c.96]
Производная функции распределения вероятностей непрерывной случайной величины равна плотности распределения вероятностей этой случайной величины, т. е. [c.61]
Аналогично в рассмотренном выше примере, если рассматривать рост студентов А в качестве значений случайной переменной Н, то при достаточно большом числе наблюдений относительные частоты появления значений hk в интервале h
В математической статистике широко используются квантили и процентные точки распределения случайной величины. Пусть случайная величина X имеет непрерывную функцию распределения F(x) и пусть задано число 0 < q < 1. Квантилъю уровня q (или q- квантилъю) распределения F(x) называется такое число uq, что F(uq) = Р(Х . uq) = q. Если величина X дискретна, то может случиться, что такого числа uq либо не существует, либо их бесконечно много. Но всегда можно найти два числа x q < xq такие, что F(x ) q, F(x ) > q. Тогда g-квантиль определяется как любое число, лежащее между x q и х . [c.512]
Для непрерывной случайной величины в (110) Р есть не вероятность, а совместная функция плотности распределения, вспомните, что для непрерывной х вероятность х быть в точности равной к есть 0. КПОВ годится для непрерывных и для дискретных переменных [c.164]
Определение 3. Последовательность случайных величин Х Хз,..., имеющих функции распределения F (x), FI(X),. . ., сходится по распределению к случайной величине X с функцией распределения F(x), (dlimn 00Xn = X) или Хп — > X (d = distribution), если linin- oo Fn(x] = F(x) в каждой точке х, где функция jP непрерывна. [c.529]
Смотреть страницы где упоминается термин Функция распределения случайной величины Непрерывные случайные величины
: [c.308] [c.184] [c.536] [c.514] [c.184]Смотреть главы в:
Эконометрика -> Функция распределения случайной величины Непрерывные случайные величины
