| Рис. 32. Кривая распределения плотности случайной величины |  |
| Рис. 33. Функция распределения для равномерной плотности случайной величины | 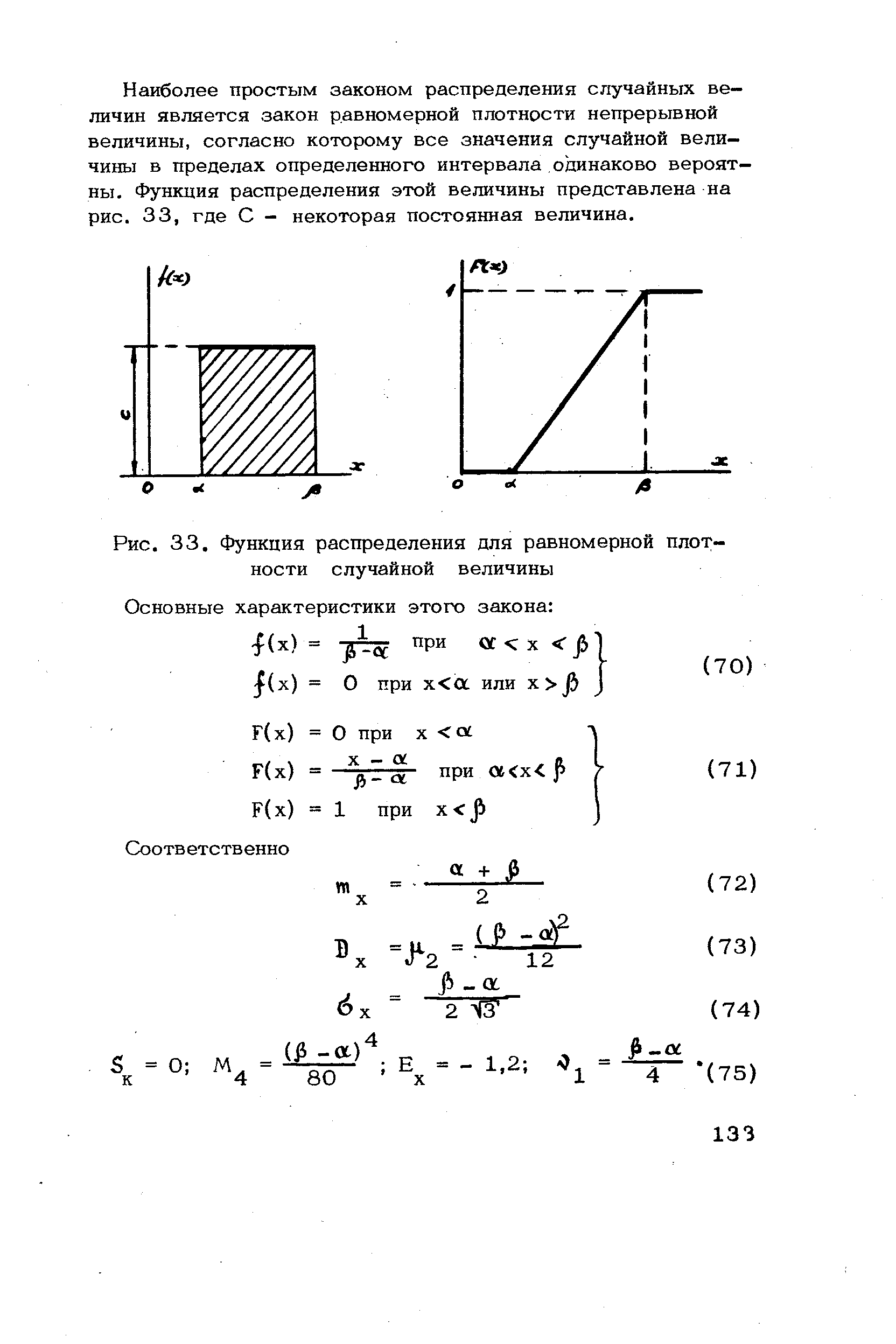 |
| Рис. 34. Распределение плотности случайной величины по нормальному закону распределения | 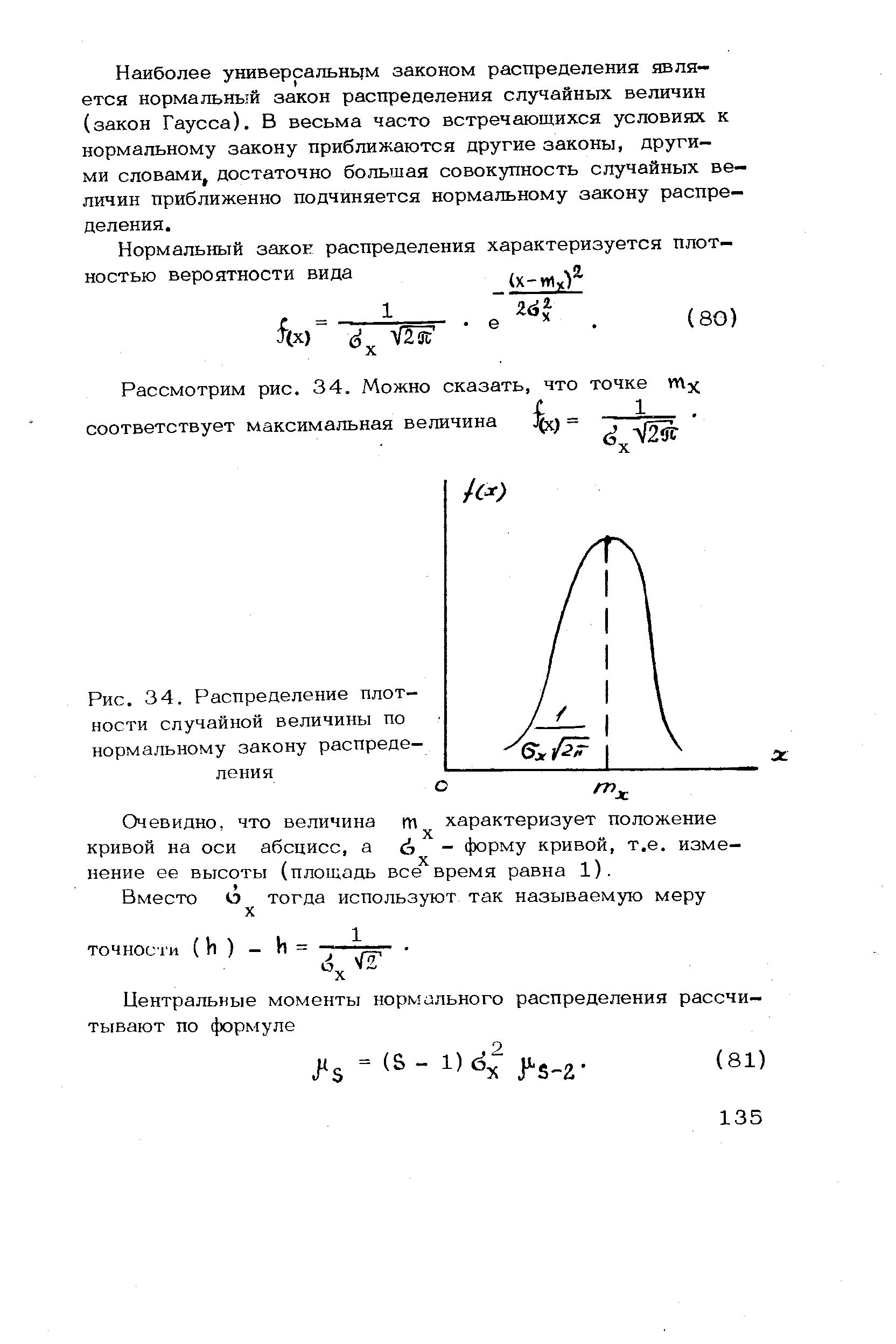 |
Плотность случайной величины S, при 0 < х < со пропорциональна показательной [c.45]
Доказать, что плотность случайной величины (Х(И) = max i, 0,2,. .., а равна пх"л. 1. Доказать, что плотность Схе х, д е[0, 1] можно преобразовать к виду [c.60]
Вследствие совместного влияния случайных и систематических факторов технологические параметры и параметры продукции являются случайными величинами. Они обычно распределены по нормальному или усеченному нормальному закону с плотностью распределения f(x) ( - )] [c.149]
Стохастическое описание. Такая форма описания используется, в тех случаях, когда факторам неопределенности z = (zi,z2,...) можно приписать вероятностный, случайный характер. Случайные факторы z формализованы, если задана их плотность вероятности. Наиболее подробно исследован в научно-технической литературе случай нормального распределения a(z)e yV(M(z),D(z)), которое полностью определяется вектором математического ожидания A/(z) и ковариационной матрицей D(Z). Некоторые специалисты рассматривают ситуацию, когда известна плотность вероятности, как детерминированную, ввиду того, что плотность вероятности является исчерпывающей характеристикой случайных величин. [c.46]
Функция плотности вероятностей в каждой точке т] имеет следующий смысл вероятность того, что величина у примет значение из интервала (ц, f +dt ), приблизительно равна f(i )dr. Функция Р(ц) (или /(т))) содержит всю имеющуюся информацию о величине у, которая в данном случае называется случайной величиной. Можно, например, подсчитать среднее значение величины у . [c.153]
Непрерывная случайная величина может принимать все возможные значения и задаваться в виде функции плотности вероятности. Одним из наиболее простых примеров служит величина, равномерно распределенная по некоторому интервалу, т.е. принимающая все значения из этого интервала с равной вероятностью и не принимающая значений вне этого интервала. [c.262]
В формуле для определения математического ожидания непрерывной случайной величины вместо вероятности используется функция плотности вероятности [c.263]
Пусть имеется р объясняющих переменных Х, ..., Хри зависимая переменная Y. Переменная Y является случайной величиной, имеющей при заданных значениях факторов некоторое распределение. Если случайная величина Y непрерывна, то можно считать, что ее распределение при каждом допустимом наборе значений факторов (х, х ,..., хр) имеет условную плотность [c.11]
Плотностью вероятности (плотностью распределения или просто плотностью) ф(х) непрерывной случайной величины X называется производная ее функции распределения [c.30]
Пример 2.7. По данным примера 2.6 найти плотность вероятности случайной величины X. [c.31]
Свойства плотности вероятности непрерывной случайной величины [c.31]
Вероятность попадания непрерывной случайной величины в интервал [a,b] равна определенному интегралу от ее плотности вероятности в пределах от а до Ъ (см. рис. 2.2), т.е. [c.31]
Функция распределения непрерывной случайной величины (см. рис. 2.3) может быть выражена через плотность вероятности по формуле [c.31]
Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице [c.32]
Непрерывная случайная величина X имеет равномерный закон распределения на отрезке [а, Ь], если ее плотность вероятности постоянна на этом отрезке и равна нулю вне его, т.е. [c.34]
Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения с параметром Я,, если ее плотность вероятности имеет вид [c.34]
Плотностью вероятности (плотностью распределения или совместной плотностью) непрерывной двумерной случайной величины (X,Y) называется вторая смешанная частная производная ее функции распределения, т.е. [c.37]
Свойства плотности вероятности двумерной случайной величины q>(x, у) аналогичны свойствам плотности вероятности одномерной случайной величины [c.37]
Условные плотности вероятности <ру(х) и ух(у) двумерной случайной величины (X, Y) определяются по формулам [c.37]
Случайная величина (случайный вектор) (X, Y) называется распределенной по двумерному нормальному закону, если ее совместная плотность имеет вид [c.40]
При каком значении параметра С эта функция является плотностью распределения некоторой случайной величины Найти математическое ожидание и дисперсию случайной величины X. [c.49]
Определить плотности вероятности и функции распределения случайных величин X и Y. Найти Р(Х> 0,05), P(Y< 100). [c.49]
Написать выражения плотности и функции распределения случайной величины X. Найти вероятности Р(Х < 15,3), Р(Х > 15,4), Р( 4,9 < X < 15,3), Р(Х- 5)<0,3 квантиль о 6, 30%-ную точку распределения X. С помощью правила трех сигм определить границы для значения случайной величины X. [c.49]
Следовательно, плотность нормально распределенной случайной величины у [c.63]
A5/S (см. также следующий раздел). Эту характеристику по /-му ресурсу можно задавать величиной Е] — математического ожидания недопоставки АР/Р°. В случае непрерывной функции эластичности ф/ при известной плотности распределения (k.S ISj) случайной величины A5 75j она выражается так [c.29]
В результате анализа, проведенного методом Монте-Карло, эксперт получает значение ожидаемой чистой приведенной стоимости проекта и плотность распределения этой случайной величины. Однако этих данных недостаточно для того, чтобы аналитик установил, действительно ли прибыльность проекта настолько велика, что компенсирует риск по проекту, оцененный стандартным отклонением и коэффициентом вариации. Ряд исследователей избегает использования данного метода ввиду сложности построения вероятностной модели и множества вычислений, однако при корректности модели метод дает весьма надежные результаты, позволяющие судить как о доходности проекта, так и о его устойчивости (чувствительности). [c.252]
Избыточно закупленный товар приносит дополнительные издержки а(1)руб./т. Дефицит товара влечет потери а(2) руб./т. Требуется определить т — предпочтительный размер закупаемой партии товара, если потребность при розничной реализации является случайной величиной и описывается функцией /(s) — плотностью распределения вероятностей. [c.90]
В стохастической коммуникационной системе ввод энтропии осуществляется при следующих предварениях. Каждая частица случайным образом проходит по определенной коммуникации (/, /), а следовательно, случайным, образом избирает величину характеристики Ягу данного канала, поэтому многократные повторения этого выбора можно интерпретировать как эксперименты над случайной величиной Я, в каждом из которых реализуется некоторое ее значение h =Я,-у с вероятностью Pij. Тем самым, при вероятностной схеме можно говорить о существовании некоторой плотности вероятности f(h) случайной величины Я, информированность о которой, в общем случае, различна. [c.105]
Плотность вероятности случайной величины 105, 106 Полиномиальное распределение 105, [c.228]
| Рис. 4.2.3. Вид плотности распределения для суммы логарифмически нормально распределенных случайных величин | 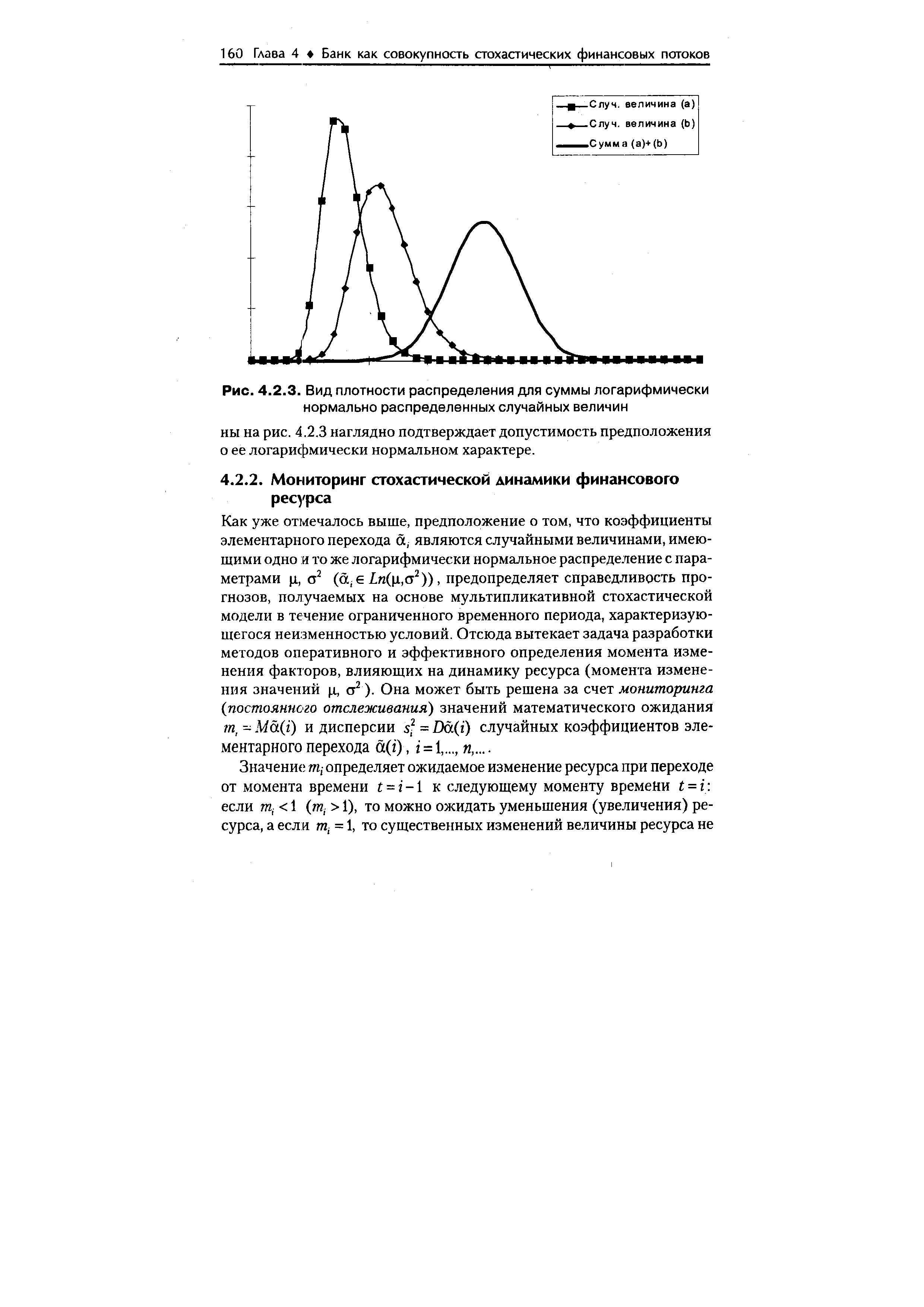 |
Знание плотности (4.4.33) случайной величины т( 0, ) позволяет найти ее математическое ожидание [c.190]
Принимаем, что плотность распределения смешанных случайных величин стремится к нормальному закону распределения. Предельную точку кривой нормального распределения выражаем через функцию Лапласа [c.91]
Предполагается, что такие необходимые понятия теории вероятности, как случайная величина, вероятность, зависимые и независимые случайные величины, формула Байеса и функция распределения плотности вероятности, известны читателю. Необходимые сведения могут быть найдены в работе [c.253]
Для непрерывной случайной величины, заданной своей плотностью вероятности q>(x), математическое ожидание и дисперсия равны [c.19]
Плотность вероятности <р(х) есть предел отношения вероятности того, что случайная величина X примет значение, лежащее между х и х+Ах, к величине интервала Ад при Ax- 0 рис. 4), т. е. [c.23]
Здесь вместо математического ожидания и дисперсии случайной величины взяты ее статистические моменты. Назовем закон распределения случайной величины Я, заданной плотностью /(Я) теоретическим. Зная, закон распределения, можно найти теоретические вероятности попадания в каждый из ин- [c.197]
Пусть далее точное число Л/ объектов в области поиска заранее неизвестно. Предполагается известной лишь производящая функций- соответствующей случайной величины Ц, (z)= 2Lp(N= )i.. Каждый из объектов поиска характеризуется своим 1 —мерным вектором значений параметров X = (X , .,.Х . Априорная информация о, значениях параметров каждого из объектов задается t —мерной плотностью распределения . / °(л L) X Lez j 7 < R г (I - J, < ,.,. N). Пару V/o (2.) ffaj будем называть априорным состоянием природы. [c.79]
Асимметрия служит для оценки симметричности распределения случайной величины относительно средней. Если асимметрия — положительное число, распределение имеет сдвиг в сторону положительных значений, иначе — в сторону отрицательных значений. Эксцесс является характеристикой остроконечности или сглаженности кривой распределения плотности вероятности случайной величины. Эксцесс равен нулю для нормального распределения, положителен для остроконечных и отрицателен для сглаженных по сравнению с нормальной плотностью распределения. [c.462]
Для того чтобы охарактеризовать центр распределения логарифмически нормальной случайной величины a, можно использовать наряду с уже вычисленным математическим ожиданием Ma моду (локальный максимум плотности /(a a)) тос1а = ехр(ц-ст2) и [c.182]
Предполагается, что поступление нефтепродукта к поставщикам Qftl, потребление нефтепродукта потребителями /< и время движения нефтепродукта Та — величины случайные, а fkt №i) fk2 (Vftz) и fd(Td)—плотности распределения величин [c.88]
Матем этическое ожидание и дисперсия непрерывной случайной величины с плотностью вероятности <р(х) определяются соответственно по формулам [c.23]
