Рассмотрим линейную модель общего вида [c.350]
Линейная модель общего вида, I 351 [c.351]
ЛИНЕЙНАЯ МОДЕЛЬ ОБЩЕГО ВИДА, II [c.354]
Здесь A (t), A2(t), i(t), 2(t — заданные матрицы, элементы Которых зависят от времени, a(t) и b(t) — заданные векторы, также зависящие от времени. Соотношение (3.17) является линейным дифференциальным уравнением, описывающим изменение состояния системы, а (3.19) — представлением множества УШ. Как и в статическом случае, исследование линейных систем является более простой задачей, чем анализ модели общего вида. К линейным моделям близки по свойствам модели типа (3.17), (3.18) с ограничениями общего вида (3.16) в том случае, когда множество Y(t) при каждом t выпукло. [c.37]
В этой главе рассматривается линейная регрессионная модель общего вида [c.320]
Решение широкого класса планово-экономических задач основывается на моделях линейного программирования. В наибольшей степени методы линейного программирования получили применения в расчетах оптимальной производственной программы НПЗ [1 — 2]. В, общем виде задача оптимизации производственной программы нефтеперерабатывающего предприятия записывается в следующем виде / [c.96]
Множество допустимых значений переменной х, которое обозначим через X, для модели (3.3) является многогранным. Можно сказать, что рассматриваемые линейные статические модели имеют общий вид [c.32]
Тем не менее методы линейного программирования зачастую могут плодотворно применяться в целях оптимизации планирования, когда для оптимума достаточно одного критерия и его экстремального выражения. Схема математической модели в самом общем виде представляется следующей. [c.232]
| Рис. 12. Общий вид матричной модели организации строительства линейной части трубопровода, | 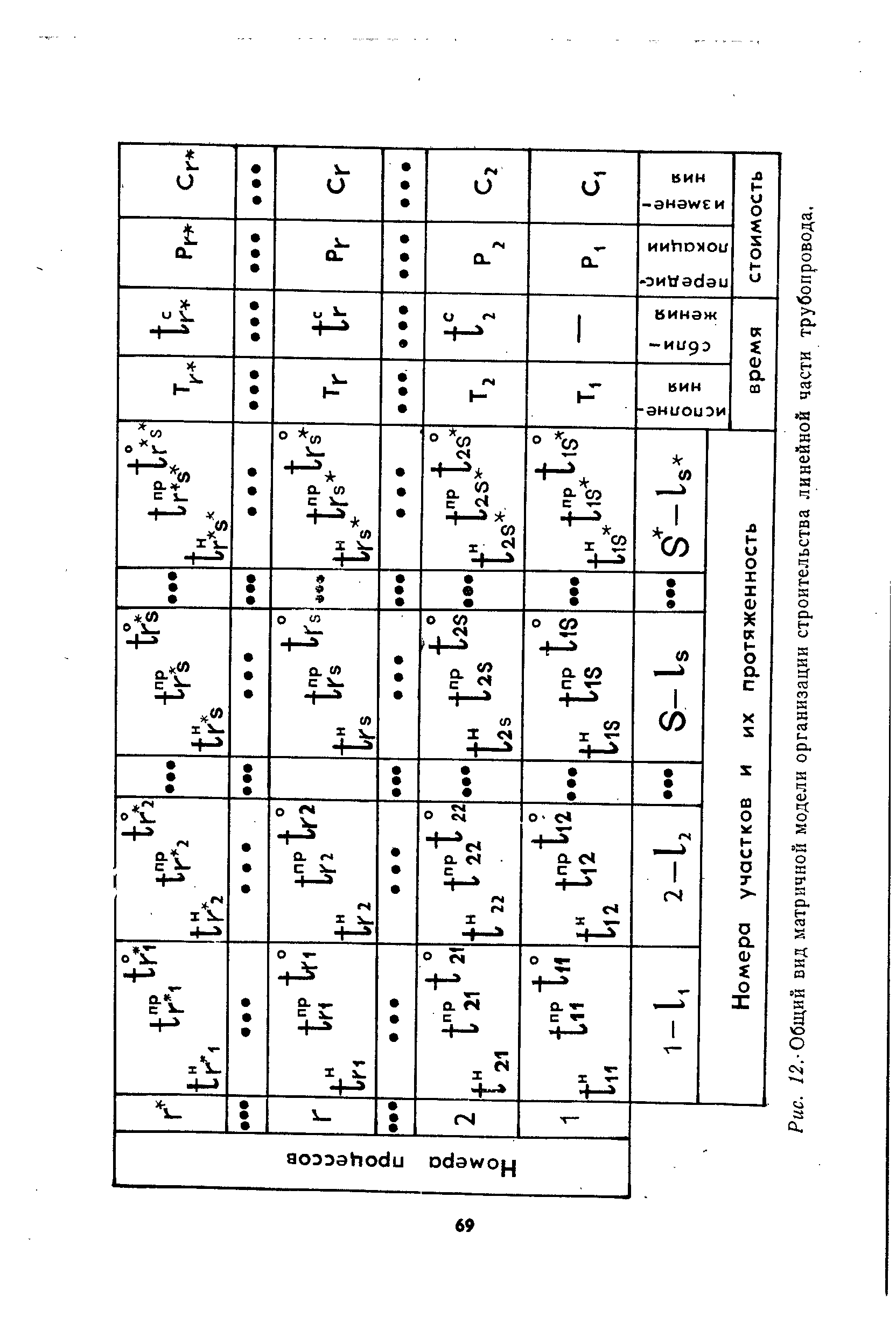 |
Статическая модель оптимизации прикрепления потребителей к поставщикам. Основной математической моделью оптимального прикрепления потребителей к поставщикам является так называемая транспортная задача линейного программирования, которая в общем виде формулируется следующим образом [c.524]
Мы рассматривали стохастические аналоги задач линейного программирования. Как легко видеть, детерминированные эквиваленты задач линейного программирования со случайными параметрами условий, соответствующие, например, моделям с вероятностными ограничениями, представляют собой, вообще говоря, задачи нелинейного, а иногда и невыпуклого программирования. Поэтому в стохастическом программировании обычно несущественно, порождена ли стохастическая задача линейной или нелинейной экстремальной задачей. Если не ограничиваться стохастическими аналогами линейных моделей, можно привести более общую запись задачи стохастического программирования, объединяющую различные постановки стохастических задач. [c.10]
Структура оптимизационной модели состоит из целевой функции, области допустимых решений и системы ограничений, определяющих эту область. Целевая функция в самом общем виде, в свою очередь, также состоит из трех элементов управляемых переменных, неуправляемых переменных и формы функции (вида зависимости между ними). Если все функции, описывающие некоторую экономическую ситуацию линейны, то имеем задачу линейного программирования, к которой и будет сведена задача игры с природой о нахождении оптимального ассортимента продукции, выпускаемой швейным производством. [c.23]
Этап 4 (определение класса допустимых решений). Главной целью исследователя на этом этапе является определение общего вида, структуры искомой связи между Y и X, или, другими словами, описание класса функций F, в рамках которого он будет производить дальнейший поиск конкретного вида интересующей его зависимости (см. задачи а) и 3 в В.1). Чаще всего это описание дается в форме некоторого параметрического семейства функций / (X в), поэтому и этап этот называют также этапом параметризации модели. Так, определив в примере В.1, что поиск зависимости среднедушевых семейных сбережений //ср от величины их среднедушевого дохода х мы будем производить в классе F = (60 + QI линейных функций, мы тем самым завершили четвертый этап исследования (но конкретных числовых значений параметров 00 и 0 мы к этому моменту еще не знаем). [c.49]
Таким образом, при р Ф 1 оценка (14.3) несостоятельна. 14.1.3. Общая линейная модель. В данной главе мы будем изучать линейную модель вида [c.404]
Запишем общую линейную модель (14.7), (14.8) в следующем виде [c.421]
При нахождении значений параметров степенных моделей для упрощения составления программы экономико-математические модели приводятся в удобные линейные функции путем логарифмирования. В общем виде степенная зависимость после логарифмирования имеет вид [c.77]
Кроме того, во многих организационных задачах значения переменных должны быть целочисленными. Например, при выборе числа машин, бригад и т.п. дробные значения переменных теряют физический смысл. Между тем, если даже ограничения и целевая функция имеют вид (7.31) и (7.32), но вводится ограничение на целочислен-ность переменных, такую задачу по сложности решения можно отнести к категории нелинейных. Однако в литературе такие задачи называют задачами целочисленного линейного программирования, общая модель которых имеет вид [c.248]
Большим достижением в области функциональных моделей явилось доказательство разрешимости для вычислительных моделей, описанных в [5,11] и реализованных в виде тиражируемой системы планирования ПРИЗ [5.12], а также получение весьма обнадеживающих оценок сложности решения указанных выше четырех основных проблем, связанных с функциональными моделями. В специальном языке описания спецификаций все эти задачи можно решать с линейной сложностью [5.13 5.14]. Отметим, что функциональные модели в последнее время активно используются при решении важной для приложений задачи — автоматического синтеза программ по исходному описанию, которая ставится в более общем виде, чем в рассмотренных нами функциональных моделях [5,15]. [c.269]
В предыдущих главах рассматривались различные математические модели задач линейного программирования. В некоторых из них, например, транспортной закрытого типа, ограничения были представлены уравнениями, а в некоторых — открытой транспортной задаче, задаче размещения и распределительной — часть ограничений задавалась в виде уравнений, а другая — в виде неравенств. Всякая система неравенств может быть сведена к системе уравнений путем различных преобразований и представлена в общем виде системой [227] линейных уравнений с неизвестными [c.293]
Линейная модель множественной регрессии имеет общий вид [c.134]
Метод линейного программирования применяется в случаях, когда зависимости между факторами линейные и характер их не меняется со временем. Этот метод предполагает наличие нескольких альтернативных вариантов решения задачи, из числа которых и определяется лучший (оптимальный). В общем виде математическая модель оптимизационной задачи выглядит следующим образом [c.16]
С помощью регрессионного анализа факторы динамики хлебных цен можно объединить в одно уравнение, придав каждому фактору вес в соответствии с его размерностью и влиянием на хлебные цены. В предельно обобщенном виде уравнение множественной линейной регрессии выразит взаимосвязь хлебных цен с их факторами. Например, для 5-факторной модели общей динамики хлебных цен 1801 — 1914 гг. уравнение следующее у = 2,3 + 0,531 хг + Н-0,207 24-0,229 3+0,00709 4+0,0044 хь, где у— хлебная цена конкретного года, хг — величина денежной массы этого года, л 2 —мировые цены предыдущего года, х3 — валютный курс этого года, х4 — урожай этого и предыдущего года, хъ — экспорт хлеба этого года. [c.218]
Модели оптимизации экономики имеют целью добиться наибольшей результативности (эффективности) использования имеющегося потенциала и ресурсов. Любая экономико-математическая модель — это воспроизведение связей между экономическими явлениями и процессами. Критерии оптимального плана могут быть разными, поэтому в общей форме подразумевается оптимальное сочетание цели и средств социалистического производства за счет интенсивного использования всех имеющихся возможностей. Целевая функция и ограничения выражаются в математическом виде, и решение их методами линейного программирования позволяет найти оптимальный вариант. [c.73]
Модель (3.8) — общее представление нелинейной статической модели с конечным числом ограничений. Так же, как и в случае линейных систем, модель (3.8) можно представить в виде (3.7), только теперь множество X уже не является многогранным. [c.33]
При прогнозировании объема ресурсов бюджета на перспективу следует использовать глубокий экономический и статистический анализ сложившихся тенденций, позволяющий в среднем с определенной степенью вероятности нивелировать влияние множества факторов, выявить наиболее общее в совокупности тенденций. Качественный анализ показал, что статистические модели, с помощью которых определяются ресурсы федерального бюджета, дали хорошо согласующиеся данные, касающиеся ею объема на ближайшую перспективу. Уравнения регрессии с указанными выше двумя переменными величинами имеют линейный вид [c.152]
В модели учитывается также конкуренция между различными типами энергоресурсов, исходя из линейного приближения, согласно которому спрос пропорционален разности цен на теплосодержание и доле потребляемых ресурсов в общей структуре энергопотребления. Общий рост производства энергии задается в виде тренда в рамках сценарного подхода. [c.70]
Идея агрегативного подхода в целом весьма продуктивна до тех пор, пока идет формализация понятий сложной системы и введение универсальной модели сложной системы под названием агрегат . Как только вводится единое понятие сложной системы агрегат , сразу возникает желание обкатать его на различных математических схемах и рассматривать его как нечто универсальное. Однако это универсальное понятие не идет дальше каждой из рассматриваемых математических схем или теорий, будь то теория линейных систем, систем, описываемых дифференциальными уравнениями, конечных автоматов и т.п. Этот подход может привести только к обобщению указанных математических схем в более общую теорию, что само по себе продуктивный и интересный предмет математических исследований, не имеющий, однако, ничего общего с развитием теории имитационного моделирования сложных систем. Вообще, когда мы говорим об имитационном моделировании, то имеем в виду моделирование исключительно сложных систем, так как простые системы легко моделировать практически любым математическим аппаратом. [c.282]
Рассмотрим общую модель линейной (относительно оцениваемых параметров в) регрессии в виде [c.208]
ИЗДЕРЖКИ СОВОКУПНЫЕ - сумма общих издержек предприятия за отчетный период, базируясь на которой можно исчислять средние издержки и предельные издержки. Под функцией совокупных издержек принимают модель динамики этих затрат в зависимости от объема производимой продукции. Различают два вида функций совокупных издержек линейную функцию и S-образную кривую. В первом случае прослеживается связь между израсходованием факторов производства и объемом продукции. Другая зависимость базируется на предположении, что сначала происходит снижение издержек, а потом пропорционально объему они прогрессивно возрастают. [c.240]
Рассмотрим линейную регрессионную модель общего вида (г/, Х/3, r2V), где X может не быть матрицей полного ранга по столбцам и V может быть вырожденной. [c.346]
Корреляционная связь — это вероятностная зависимость, которая Проявляется только в общем виде и при большом количестве наблюдений. Данная связь выражается уравнениями регрессии различного вида. Например, однофак-торные модели могут базироваться на линейном уравнении [c.321]
Ирония заключается в том. что драматическая волна промышленных банкротств в ходе потрясений 70-х и 80-х годов породила новые идеи об организации промышленности будущего. Эти идеи очень нелегко примирить с линейной моделью инноваций и американской моделью вертикальной интеграции. Новые идеи проясняют пост-фордистское будущее капиталистического роста и накопления лучше, чем рационализация, концентрация и вертикальная интеграция крупных корпораций массового производства (фордизм). В общем виде новые доводы сводятся к тому, что в условиях фордизма крупные корпорации были в состоянии контролировать большой диапазон деятельности, от НИОКР и производства до маркетинга, выигрывая конкуренцию со старыми ремесленными малосерийными производствами. Однако более специализированные рынки (ниши) растут вместе с более искушенными покупателями (и компаниями-пользователями), когда качество и возможность выбора ценятся больше, [c.148]
Подробное описание методов статистического анализа временных рядов выходит за рамки этой книги. Мы вкратце рассмотрим традиционные подходы, выделяя при этом обстоятельства, которые имеют прямое отношение к предмету нашего изложения. Начиная с пионерской работы Юла [295], центральное место в статистическом анализе временных рядов заняли линейные модели ARMA. Со временем эта область оформилась в законченную теорию с набором методов — теорию Бокса-Дженкинса (см. [48] ). В этом подходе модель задается двумя компонентами, характеризующими авторегрессию и скользящее среднее. Общая формула для процесса с авторегрессией и скользящим средним порядка (p,q) имеет вид - - [c.57]
В настоящей главе обсуждаются методы построения решающих правил для одноэтапных задач стохастического программирования, а для отдельных моделей приводятся и явные выражения для решающих правил. В 1 рассматриваются частные модели первого класса, в которых предполагается, что решающие правила — линейные функции случайных составляющих условий задачи. Вычисление параметров решающих правил сводится к задачам выпуклого программирования. Параграф 2 посвящен изучению. М-модели с вероятностным ограничением общего вида. Относительно решающего правила л (со) не делается никаких предположений, кроме того, что л (со)—измеримая вектор-функция на множестве X произвольной структуры, на котором она определена. В 3 метод построения решающих правил из предыдущего параграфа обобщается на М-модель с конечнозначным ограничением — с условием, ограничивающим математическое ожидание случайной функции от х, принимающей конечное число значений. Таким условием может быть аппроксимировано любое статистическое ограничение. В 4 построены решающие правила (точнее, решающие таблицы) дляч Р-мо-дели с вероятностными ограничениями общего вида. В 5 рассматривается стохастическая задача со смешанными ограничениями. Эта модель отличается от задачи 4 дополнительными условиями, которые могут существенно изменить структуру решения. В 6—8 построены решающие правила для одноэтапных задач стохастического программирования со статистическими ограничениями достаточно общего вида. Модель, изученная в 6, представляет собой стохастический аналог общей задачи линейного программирования с двухсторонними ограничениями. Модель из 7 — стохастический аналог общей задачи квадратичного программирования. Модель, исследованная в 8, является стохастическим аналогом частной задачи выпуклого программирования с квадратичной целевой функцией и квадратичными ограничениями. Заключительный параграф главы ( 9) посвящен итеративным методам построения решающих правил одноэтапных задач стохастического программирования. [c.84]
Общая математическая модель линейной регрессии имеет вид Y = X + е, где Y — (п X 1)-вектор наблюдений, X = (Xi... Хп) — (п X р)-матрица плана экспериментов, Xk — регрессор й-го наблюдения, в — (р X 1) -вектор неизвестных параметров, s — (п X 1) — вектор случайных ошибок. В классической постановке задачи линейной регрессии предполагается, что г N (0, сг21п), где 1П — (п X п)-единичная матрица. Оценки по методу наименьших квадратов (мнк-оценки) отыскиваются из условия минимизации по 0 величины Y — Х0 . Когда Х Х =т О (ранг X равен р), [c.249]
Следовательно, индивидуальные значения yi представляются в виде суммы двух компонент - систематической (р0 + piXj) и случайной (si), причина появления которой достаточно подробно рассмотрена в разделе 4.2. В общем виде теоретическую линейную регрессионную модель будем представлять в виде [c.99]
В задачах линейной фильтрации и прогноза случайные процессы L, и g связаны соотношением вида (5.1). Взаимнооднозначное соответствие между i Li и P(ii, т)еЯ (см. теорему 2.1.) позволяет переформулировать задачи I и II и общую модель (5.2) — (5.4) в терминах функций веса. Критерий качества R прогноза — функция первых и вторых моментов ошибок и матрицы k искусственного рассеивания — [c.323]
Агрегативная математическая схема имитационного моделирования, введенная Н.П. Бусленко, позволила обобщить многие частные имитационные подходы и создала предпосылки к разработке общей теории имитационного моделирования при использовании различных форм математического описания объектов моделирования. Ценность агрегативного подхода заключалась не только в математическом описании сложной системы в виде некоторого агрегата или элементарного блока имитационной модели, во введении кусочно-линейных и кусочно-непрерывных агрегативных схем, в математическом описании сопряжения и функционирования агрегатов. Главная заслуга школы Н.П. Бусленко состоит в формировании имитационного мышления, т.е. в отрицании многих догм, свойственных различным математическим подходам при моделировании объектов. Так, например, отброшена догма единой целевой функции для объекта моделирования. При имитационном подходе их может быть столько, сколько нужно. Не мешают проблемы стремления функций к бесконечности или нулю, проблемы гладкости и непротиворечивости. Не вызывает особых проблем нестационарность, неординарность, наличие последействия в используемых потоках случайных событий. Не приводит к вычислительным проблемам использование законов распределения с изменяющимися параметрами и многое другое. [c.5]
Этот тип тренда может описывать также ситуацию чисто сезонного тренда 6te лийейного элемента. Однако в общем случае для модели этого типа Характерно присутствие сезонного тренда, который в свою очередь мо ет линейна расти. Линейный и сезонноаддитивный тренды изображены на рис. 2.3. Как видим, из года в год повторяются два пика. [c.28]
Нет никаких оснований предпочесть этому распределению дохода распределение yfbt , если, конечно, не расширить модель, включив в нее в явном виде предпочтения на множестве вменяющих векторов или функции спроса и т. п., т.е. если не отказаться от решения задачи распределения на основе чисто производственного подхода. Таким образом, приходим к выводу, что в частном линейном случае в условиях товарного производства множители Лагранжа могут выполнять распределительную функцию цен, но вектор, составленный из множителей Лагранжа, не является единственным вменяющим вектором и из условий задачи оптимального планирования не следует, что предпочтение надо отдать именно множителям Лагранжа. В общем нелинейном случае вектор, составленный из множителей Лагранжа, не является вменяющим и множители Лагранжа не могут выполнять распределительную функцию цен. [c.65]
Таким образом, возникает следующая задача. Задан комплекс работ в виде сетевой модели. Каждой работе (i,j) соответствуют длительности t., неизвестные дополнительные средства (прямые затраты ..), которые можно вложить в работы с целью сокращения их длительностей ограничения /г.. на величины х. некоторые коэффициенты продолжительности работы коэффициент прямых затрат с,-,- = (с гу - с, -,- ) /( , -,- - t j ), где индексы и " — соответственно максимальное и минимальное значения соответствующих параметров. Величины с у и с" у получают суммированием составляющих прямых затрат по каждому из вариантов выполнения работы. Пусть общая продолжительность разработки Т велика и требуется уменьшить ее до удовлетворения неравенства Т < Тг, где Тг — заданное ограничение. Зависимость новой длительности работы ц от прежней t.. задана в виде Ц =tij(i-dijXij). Тогда возникает задача нахождения таких дополнительных вложений средств в работы, чтобы выполнялись условия [c.279]
Обобщение результатов работ [38, 47, 56, 62] позволило нам разработать укрупненную схему, отражающую научную базу в виде моделей и методов теории логистики, приведенную на рис. 3.2. Понятие укрупненная использовано в том смысле, что названия некоторых методов являются общими для целой гаммы дисциплин. Например, блок оптимальное программирование включает линейное, целочисленное, нелинейное (выпуклое), динамическое программирование. А блок теория принятия решений объединяет многообразие задач выбора разовый, повторный, индивидуальный, групповой, однокритериаль-ный, многокритериальный, в условиях определенности, неопределенности и др. [c.44]
