Выравнивание временных рядов 58 Вырожденная задача 59 Вырожденная матрица 59 Высказывание 175 Выходная информация 134 Выходные величины 59 Выходные данные 232 Вычислимая алгоритмическая проблема [c.462]
Для исследования моделей комплекса Регион применяются новые алгоритмы улучшения и приближенно-оптимального синтеза управления с использованием достаточных условий сильного и слабого локального минимума [Кротов и др., 1973 Гурман, 1977 Гурман и др., 1983 Модели..., 1981], в том числе и для вырожденных задач [Гурман, 1985 Новые..., 1981 Методы..., 1988] численные методы, связанные с преобразованием задач оптимального управления на основе теорем о совместной оптимальности [Москаленко, 1983 Методы..., 1988 Новые..., 1987] методы решения задач оптимального управления с фазовыми и смешанными ограничениями [Методы..., 1988] методы качественного анализа оптимальных траекторий [Модели..., 1981]. [c.177]
Гурман В. И. Вырожденные задачи оптимального управления. — М. Наука, 1977. [c.419]
Заметим, что мы не рассматриваем некоторых осложнений в связи с возможной в принципе вырожденностью задачи. Эта вырожденность, редко встречающаяся в практике экономических расчетов, может привести, например, к тому, что ограничение на 8s оказывается связанным одновременно с выходом s .+ 8 у и какой-то из базисных переменных й+(< >4, hj) Sy на границу до- [c.422]
Из данной интерпретации вытекает и идея метода решения вырожденных задач ЛП, получившего названия метода возмущений при выходе на вырожденный план осуществляется незначительный сдвиг вектора b и вырожденность (как это видно из иллюстрации) устраняется. [c.47]
Какие проблемы возникают при решении вырожденных задач [c.80]
ВЫРОЖДЕННЫХ ЗАДАЧ УПРАВЛЕНИЯ [c.98]
Формулировка вырожденной задачи синтеза [c.98]
В вырожденной задаче требуется определить такую скалярную функцию L(t,u,ur n), для которой уравнение Ляпунова (16) справедливо при любом допустимом векторе управления и. Это требование равносильно введению в левую часть соотношения (25) добавочного члена -0.5(м0 -иап) К и0 -м ). Так как вектор- [c.103]
Учебные заведения - структуры развивающиеся. В реальных условиях они находятся в двойственном положении. С одной стороны перед ними стоит задача сохранения собственной идентичности, а с другой, - окружение требует изменения характера их деятельности. Однако введение в старые стены принципиально новых целевых установок и содержания приводит к вырождению условий для воспроизводства эталонных качеств высшего учебного заведения и превращению его в средство решения задач текущего развития. В итоге эталонный центр деградирует, признаком чего может служить кризис его фундаментального знания. [c.60]
Если число отличных от нуля перевозок меньше т + и — 1, то план называется вырожденным. Для удобства решения задачи в этом случае вырожденный план можно преобразовать, изменив на малую величину е объем добычи нефти или размер ее потребления так, чтобы общий баланс не нарушился, промежуточные балансы уничтожались, а после нахождения оптимального плана принять е = 0. [c.72]
Ответ заключается в том, что сформулированная ЛП-задача тоже вырожденная, т.е. несколько наборов переменных решения соответствует одному и тому же значению целевой функции. Симплекс-метод сводится к одному из решений в зависимости от того, [c.141]
| Рис. 9.4. Случай, когда решение х задачи условной оптимизации является стационарной точкой ограничения f(x) = 0 (вырожденный) | 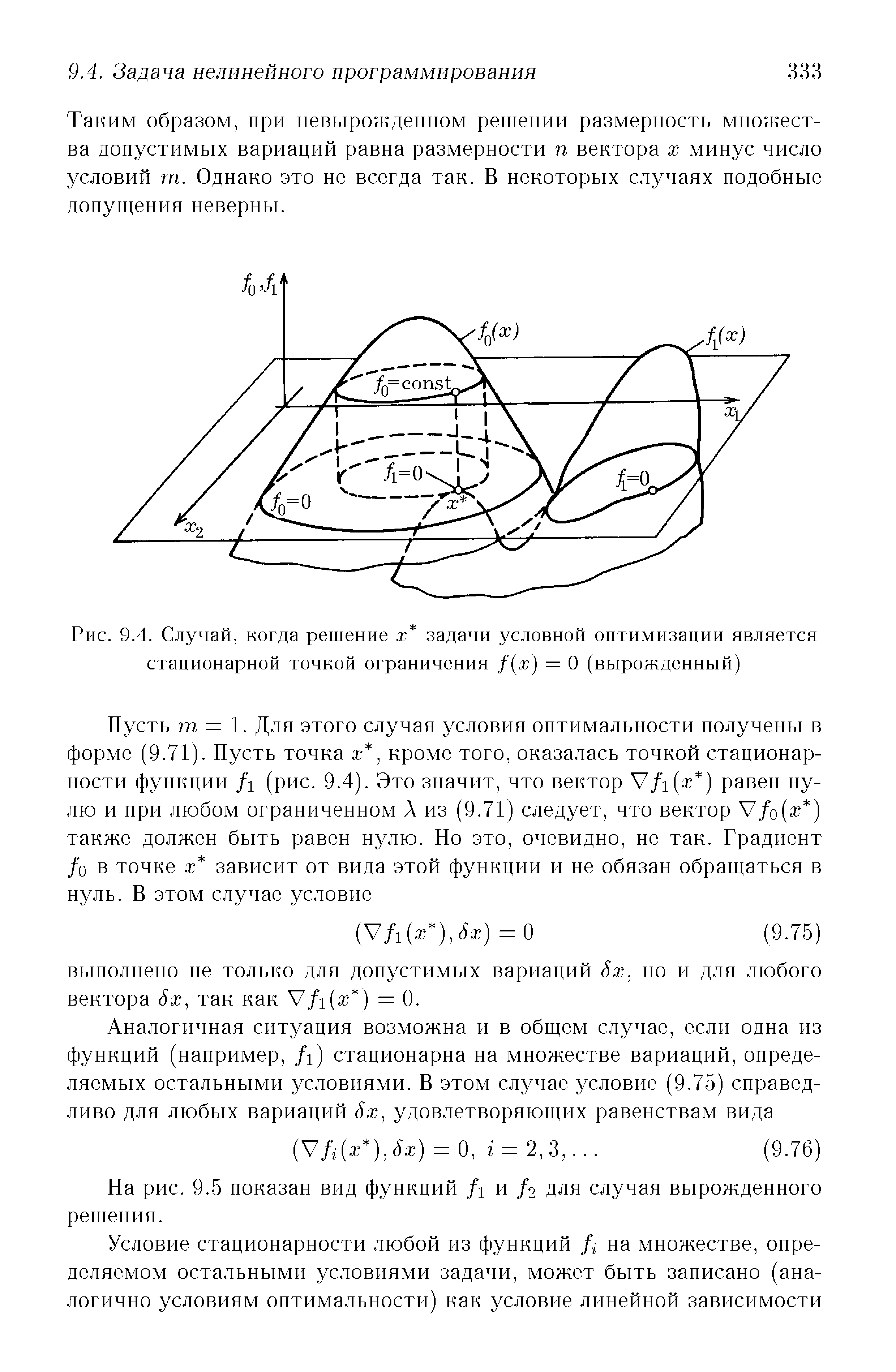 |
В оптимальности решения можно убедиться, воспользовавшись условием оптимальности алгоритма транспортной задачи. Заметим, что полученное оптимальное решение является вырожденным. [c.569]
Равенство qk = q0 означает, что в решении последней задачи X = = (xi, Xz, , XN—I, XN) компонента к <.= О, т. е. план X вырожден, и задача имеет более одного решения. [c.193]
В рассмотренной ниже модели стохастического программирования [351] ограничения задачи определяются неотрицательными квадратичными функционалами. Причем матрицы квадратичных форм, включенных в целевую функцию, и условия задачи — вырожденные матрицы ранга единица [c.116]
Специальный интерес представляет вырожденный случай многоэтапной стохастической задачи с вероятностными ограничениями, ког- [c.238]
Разбираясь в этом вопросе, нужно серьезно обсудить теоретические взгляды, изложенные в монографиях Янга [101] и Кротова и Гурмана [39]. В них подчеркивается практическая необходимость изучения вырожденных решений вариационных задач (обобщенных кривых, скользящих режимов и т. д.) и разрабатывается соответствующий достаточно сложный математический аппарат. [c.94]
ВЫРОЖДЕННАЯ ЗАДАЧА [degenerate problem] — задача линейного программирования, в которой при разложении вектора ограничений В (обозначения см. в ст. "Линейноепрограммирование") по некоторому базису а]х. ... ат по крайней мере один коэффициент оказывается равным нулю. Такая ситуация затрудняет решение задачи симплексным методом, вызывая явление "зацикливания", при котором одно и то же множество базисных решений будет периодически повторяться, а оптимальный план никогда не будет достигнут. [c.59]
См. также Ассортиментные задачи, Базисное решение, Блочное программирование, Булево линейное программирование, Ведущий столбец, Ведущая строка, Вершина допустимого многогранника, Вырожденная задача, Гомори способ, Граничная точка, Двойственная задача, Двойственность в линейном программировании, Дифференциальные ренты, Дополняющая нежесткостъ, Жесткость и нежесткость ограничений ЛП, Задача диеты, Задача о назначениях, Задача о раскрое, Задачи размещения, Исходные уравнения, Куна— Таккера условия, Множители Лагранжа, Область допустимых решений, Опорная прямая, Оптимальное распределение ресурсов, Распределительные задачи, Седловая точка, Симплексная таблица, Симплексный метод, Транспортная задача. [c.173]
СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (симплекс-метод) [simplex method] — вычислительная процедура, основанная на принципе последовательного улучшения решений — перехода от одной базисной точки (см. Базисное решение) к другой, для которой значение целевой функции больше (эти операции фиксируются в симплексной таблице). Доказано, что если оптимальное решение существует, то оно обязательно будет найдено через конечное число шагов (за исключением т.н. вырожденной задачи, при которой возможно явление "зацикливания", т.е. многократного возврата к одному и тому же положению). Название метод получил от термина " -мерный симплекс". Геометрическая интерпретация метода состоит в последовательном движении по верши) шм симплекса. [c.322]
Вектограмма 52, 95 Внебазисная переменная 419 Вторая вариация 203 Выпуклая оболочка 86, 125 Выпуклое тело, множество 369 Выпуклый конус 46 Вырожденная задача линейного программирования 171 Вычислительная технология 173, 210 [c.484]
Рассматривается задача синтеза оптимального управления для нелинейного объекта с аффинно входящими управлениями в условиях вырожденности. В качестве развития метода, связанного с минимизацией ФОР, предлагается исходную невырожденную задачу АКОР преобразовать в вырожденную задачу синтеза оптимального управления и осуществлять поиск решения на основе подходящей субоптимальной стратегии, в том числе и построения минимизирующих последовательностей, поинтервально сходящихся к оптимальному процессу исходной задачи. Для вырожденной задачи АКОР получены необходимые и достаточные условия существования оптималыюго решения. [c.98]
Теперь поставим перед собой цель свести поставленную задачу к вырожденной. Доопределим конструкцию функционала (3) таким образом, чтобы условия (4) и (5) удовлетворялись при произвольной вариации управления 8u(t). Иначе говоря, определим дополнительные условия, при которых оптимальное решение имеет место в виде пары оптимальной траектории xon(t) и любого (в рамках справедливости приведенных записей) управления uoll(t) + Su(t). Именно в этом смысле будем говорить о вырожденности задачи синтеза. [c.99]
Традиционный путь исследования вырожденных задач ОУ, состоящий в получении более тонких, но и несоизмеримо более сложных необходимых условий оптимальности [10], не снимает проблему существования и единственности решения задачи синтеза. Однако имеется большой класс задач (названных в свое время задачами АКОР), в которых эта проблема разрешима путем замены задачи Коши (4)-(5) на более простое достаточное условие оптимальности в форме уравнения Ляпунова с граничным условием, равным терминальному члену функционала (2). Формально такая замена достигается через определенную модернизацию исходной постановки задачи синтеза путем введения в функционал (2) дополнительного изопериметрического условия, имеющего энергетический смысл [11]. [c.101]
Формулировка вырожденной задачи АКОР заключается в определении такой структуры функции L(t,u,uoa), для которой, с одной стороны, вместо задачи Коши (4)-(5) используется более простое достаточное условие оптимальности в форме уравнения Ляпунова [c.101]
В. Постановка вырожденной задачи АКОР [c.103]
В сформулированной нами постановке задачи АКОР вырожденность условий оптимальности проявляется в том, что управления в уравнения объекта (11) и в функционал (27) входят линейно. Однако эта вырожденность имеет особый смысл она проявляется в результате перехода от невырожденной задачи АКОР с ФОР (24) к сингулярной, для которой регулярные признаки оптимальности исходной задачи остаются справедливыми. Поэтому в отличие от обычной постановки вырожденной задачи управления, в которой требуется найти сингулярную кривую, для предлагаемой формулировки она известна ею является оптимальная траектория, вычисляемая через соотношение (26). Однако условия существования оптимального решения при минимизации КВОР не определены, и необходимы дополнительные исследования по расшифровке и локализации [12] этих условий. [c.104]
Теорема. Для существования вектор-функции ОУ (26), доставляющей инфимум функционалу (27) вырожденной задачи АКОР при всех иеС/с/ 1", необходимо и достаточно, чтобы выполнялись следующие условия [c.105]
Гурман В.И., Дыхта В.А., Колоколышкова Г.А. Нелокальные преобразования вырожденных задач оптимального управления и импульсные режимы. - Иркутск Издательство ВЦ СО АН СССР, 1990. [c.105]
По этой матрице можно судить о тесноте связи факторов с результативным признаком и между собой. Хотя все эти показатели относятся к парным связям, все же матрицу можно использовать для предварительного отбора факторов для включения в уравнение регрессии. Не рекомендуется включать в уравнение факторы слабо связанные с результативными признаками, но тесно связанные с другими факторами. Если, например, имеем г =0,8 г = 0,65 г п = 0,88, то в регрессионное уравнение следует включить фактор х , а фактор х2 не включать, так как он тесно связан с х] (коллине-арен с я,), и его корреляция с у слабее, чем корреляция фактора , . Совершенно недопустимо включать в анализ факторы, функционально связанные друг с другом, т. е. с коэффициентом корреляции, равным единице. Включение таких пар признаков приводит к вырожденной матрице коэффициентов и неопределенности решения. В этом случае решение задачи на ПЭВМ прекращается. [c.275]
Sx = —, где Sx — выборочное среднеквадратическое отклонение, или стандартное отклонение выборки п — размер выборки) и коэффициент вариации будут меньшими и, наоборот, увеличение рассеивания надо рассматривать как повышенную погрешность данного варианта измерителя. Такой метод далеко не единственный, но самый простой метдц выбора, показателя, который может быть применен для решения довольно широкого класса экономических задач. При этом VQ — является вырожденным случаем второго способа VQ при V = 0. Однако здесь следует помнить, что эта гипотетическая оценка довольно условна. Более того, можно рассмотреть несколько других технически более сложных вариантов, например V = 0,3 V" = 0,5 V e = 1,0-и, самое главное, изучить, к каким выводам приведет каждый вариант. Вполне возможно, что несколько вариантов приведут к одним и тем же выводам и тогда можно будет говорить о более высокой степени адекватности таких вариантов. [c.70]
Поясним причины недифференцируемости функции достижимости в случае вырожденного решения. Причина заключается в том, что вырожденному решению соответствует изолированная точка а на плоскости х. На рис. 9.7, а показано расположение линий уровня, соответствующих задаче, изображенной на рис. 9.4. При замене равенства /1 = 0 на /1 = С поверхность Д перестанет касаться с плоскостью, соответствующей значению С . Если точка касания а при сколь угодно малом изменении С исчезнет, то произойдет скачок функции достижимости в сторону ее уменьшения (рис. 9.7, б). [c.340]
Условие невырожденности решения исходной задачи при использовании правила (9.134) не играет существенной роли, так как даже в случае, когда задача с условиями f(x) = 0 имеет вырожденное решение, задача с условиями /(а ) < е > 0, которая решается численно, для непрерывных функций fi(x) невырожденная. [c.360]
Четвертая часть, посвященная неравенствам, возникла благодаря нашему убеждению, что эконометристы должны легко оперировать неравенствами, такими как неравенство Коши-Буняковского (Шварца), неравенство Мин-ковского и их обобщения, а также владеть мощными результатами, например теоремой отделимости Пуанкаре. В какой-то мере глава является и историей нашего разочарования. Когда мы начинали писать эту книгу, у нас была амбициозная идея — вывести все неравенства методами матричного дифференциального исчисления. В конце концов, каждое неравенство может быть представлено как решение некоторой оптимизационной задачи. Однако эта идея оказалась иллюзией, поскольку матрица Гессе в большинстве случаев оказывается вырожденной в точке экстремума. [c.16]
Неоднозначность отображения Z ( ). Нет никаких оснований считать отображение Z (I) взаимно однозначным всюду, даже если единственность задачи Коши гарантирована. В самых простых ситуациях, как показывают примеры, возможны различные типы вырождения, например, (и-1-/ -мерная сфера в пространстве с (напомним, что (п-r tn)—размерность I) может отображаться в (п+т—1)-мерное многообразие в простран- [c.119]
