Результатом решения задачи оптимального управления капиталом будет являться разворачивающаяся во времени динамическая последовательность инвестиционных решений (оптимальная траектория управления капиталом), при использовании которой инвестор (спекулянт, трейдер) может извлечь потенциально возможную для рынка прибыль. Естественно, что оптимальность управления капиталом понимается в статистическом смысле. Это означает, что при использовании найденной стратегии управления инвестор (спекулянт) будет фактически максимизировать математическое ожидание (среднее значение) извлекаемой прибыли. [c.29]
В рамках современной теории финансовых спекуляций (см. ниже раздел 7) указанный вопрос решается на основе методологии кибернетики и теории оптимального управления. Использование указанной методологии позволяет синтезировать динамическую траекторию управления капиталом в функции времени, которая обеспечит извлечение потенциально возможной для рынка ценных бумаг прибыли. [c.107]
Требуется найти оптимальную траекторию управления динамической системой, исходя из условия обеспечения экстремума целевого функционала [c.156]
Результаты динамической оптимизации принимаемых на каждом шаге решений будут представлять собой оптимальный закон (траекторию) управления динамической системой. Так как в качестве динамической системы мы рассматриваем финансовый рынок и, соответственно, формируемый из инструментов рынка портфель инвестора, то найденный (синтезированный) закон управления портфелем инвестора будет одновременно являться оптимальной стратегией инвестиций. [c.190]
| Рисунок 2. Оптимальные траектории управления производственной системой по быстродействию х1,х2 — параметры системы и — управляющая переменная. | 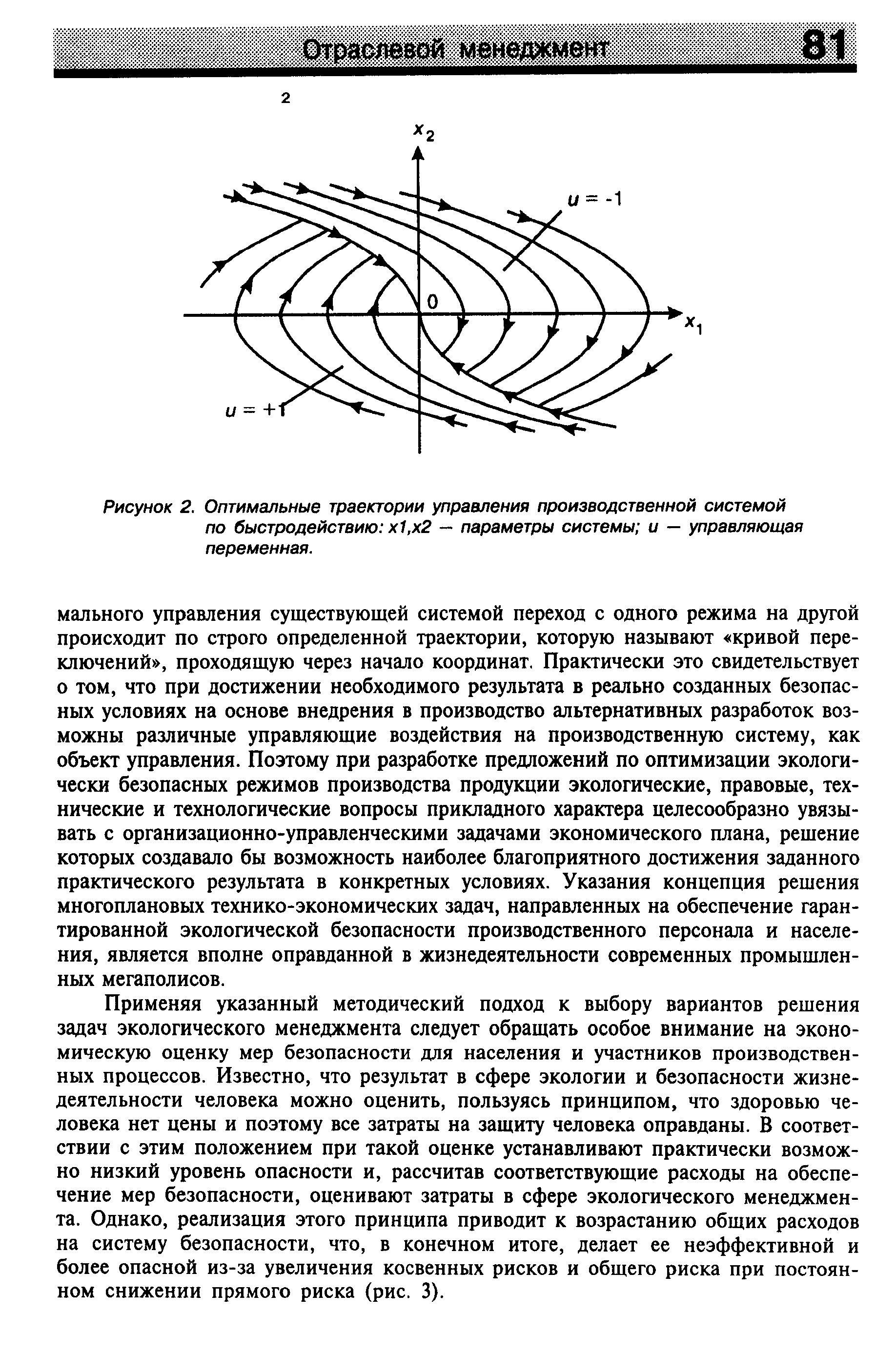 |
Если Заказчик может сформулировать критерий, по которому он количественно оценивает различные варианты развития системы, то единственные оптимальные управление и траекторию можно выбрать путем решения задачи оптимизации. Оптимизационная постановка состоит в следующем. Пусть критерий развития системы имеет вид [c.43]
В последнее десятилетие для анализа экономико-математических моделей стал широко использоваться имитационный подход, на основе которого удается преодолеть некоторые из трудностей, связанных с использованием оптимизационного подхода. В имитационном подходе, вообще говоря, не требуется заранее задавать критерий развития изучаемого объекта. Вместо него задается управление — либо в виде функции времени и (t), либо в виде функции состояния системы и (х). Подставляя эти заранее сформулированные функции в систему дифференциальных уравнений (4.5) с начальными данными (4.7), можно построить траекторию системы. Если при этом не нарушается ограничение (4.6), то управление и (t) (или и (х)) является допустимым. Сформулировав заранее некоторое число вариантов управления, можно построить траекторию системы для каждого из вариантов и представить результаты развития системы Заказчику, чтобы он сам выбрал наиболее подходящий ему вариант управления системой. В этом подходе вместо проблемы формулировки единственного критерия возникает проблема выбора вариантов управления, которые будут изучаться в исследовании. Очевидно, что такой способ исследования, называемый обычно методом вариантных расчетов, не очень экономичен. Подчеркнем, что имитация свелась к вариантным расчетам в случае уже сформулированной модели (4.5) — (4.7). В действительности же имитация, понимаемая как эксперимент с математической моделью, проводимый на основе ЭВМ, является новым мощ- [c.44]
Особенностью оптимизационного и имитационного подходов является то, что в них вместо бесконечного числа вариантов управлений и соответствующих им траекторий рассматривается один вариант управления (оптимальное — в оптимизационном подходе) или несколько (конечное число вариантов управления — в имитационном подходе). В последнее время появился еще один подход, предназначенный для оценки возможностей системы в целом, при всех допустимых управлениях — подход на основе множеств достижимости. Множеством достижимости Г (Т) для системы (4.5) — (4.7) называется множество всех таких состояний х, в которые систему (4.5) — (4.7) можно привести при помощи допустимого управления из точки х0 за время Т. Изучая множество Г (Т), заказчик может выбрать наиболее удовлетворяющий его конечный результат развития системы. [c.45]
До сих пор мы говорили об основных методах исследования систем типа (4.5) — (4.7), т. е. систем без случайных возмущений и неопределенностей. В таких моделях управление однозначно определяло траекторию системы. Если же мы будем учитывать случайные возмущения , то траектория будет зависеть от того, какие конкретные значения случайных величин реализовались. Если удастся сформулировать критерий развития системы, то его значение будет случайной величиной, распределение которой будет зависеть от управления. Методы исследования таких моделей бывают теоретическими (когда пытаются построить распределение некоторых показателей данной модели), оптимизационными (когда пытаются найти управление, приводящее к максимуму, скажем, математического ожидания критерия), и имитационными, причем в данном случае задаются не только варианты управления системой, но и варианты реализации случайных воздействий . [c.45]
Подведем предварительный итог исследования модели (4.1) — (4.6) при постоянной норме накопления s. В любом случае траектории системы асимптотически сходятся к сбалансированному росту, темп роста на котором равен темпу роста населения страны. Такой результат довольно неутешителен, поскольку потребление на душу населения при сбалансированном росте экономики остается постоянным. Возникает вопрос о том, нельзя ли добиться лучших результатов, если использовать изменяющееся во времени управление — норму накопления s (/) Проведем соответствующий анализ. Будем рассматривать модель (4.1) — (4.6) или, что то же самое, модель (4.10) — (4.12) с управлением s (f). [c.80]
Прежде всего необходимо решить проблему выбора критерия, по которому мы будем оценивать различные варианты развития экономической системы (4.10) — (4.12). При исследовании различных вариантов сбалансированного роста мы брали в качестве критерия величину с — потребление на одного трудящегося в единицу времени. Так можно было поступать потому, что на траекториях сбалансированного роста модели (4.1) — (4.6) эта величина остается постоянной. Теперь, при изменяющемся во времени управлении s (f), потребление на одного трудящегося в единицу времени также является переменной величиной. Естественно максимизировать суммарное потребление за весь период планирования, т. е. величину [c.80]
Математические модели, на основе которых осуществляется имитационный эксперимент, могут быть детерминированными и стохастическими. В детерминированной модели задание внешних воздействий однозначно определяет значения изучаемых величин. Так, в модели долгосрочного прогнозирования задание управлений sx и s2 давало возможность вычислить траектории К (t) и с (/). При использовании детерминированной модели повторение просчета при тех же значениях факторов приводило к тем же реакциям. Иное дело стохастические модели. В них реакция получается в результате взаимодействия внешних воздействий в ряде случайных чисел, которые, хотя и являются выборкой из одного и того же распределения, в силу случайности моделируемого процесса принимают разнообразные значения. В этом случае повторение просчета при тех же внешних воздействиях приведет к иному значению показателей. Так, в задаче выбора АЗС о просчетах с разными значениями случайных чисел при одном и том же варианте АЗС мы получим разные значения среднего времени простоя автомобиля (1/т) Х, и простоя оборудования Ym/Tm. Поэтому для более точной оценки интересующих заказчика величин среднего времени х простоя автомобиля и средней доли у времени простоя оборудования для одного и того же варианта АЗС проводят несколько просчетов. [c.283]
В середине пятидесятых годов Л. С. Понтрягин выдвинул так называемый принцип максимума, дающий необходимые условия оптимальности для управляемых систем типа (3.11) с ограничениями на управление типа (3.13). В дальнейшем принцип максимума был обобщен на системы с ограничениями (3.14), характерными для экономических задач (см. [90J). Принцип максимума позволяет качественно проанализировать задачу оптимального управления, выявить особенности оптимальных воздействий на систему и оптимальных траекторий движения. В том случае, когда в исследовании необходимо найти оптимальное воздействие на систему, дифференциальные уравнения (3.11) обычно аппроксимируются многошаговыми уравнениями типа (3.21) и проблема сводится к решению статической задачи оптимизации. [c.59]
Имитационные эксперименты. Имитационные эксперименты как средство анализа экономико-математических моделей начали широко распространяться в шестидесятых годах. Идея имитационного эксперимента крайне проста. Пусть система описывается с помощью динамической многошаговой модели (3.21)—(3.23) с начальным условием (3.18). Зададим некоторое управление u(t) (t — 0,. .., Т — 1) и по (3.18) и (3.21) найдем траекторию x(t) (t = 0,. .., Т). Проверим выполнение условий (3.22), (3.23). Если эти условия удовлетворяются, т. е. управление оказывается допустимым, рассчитываем значение показателей. На этом исследование одного варианта управления заканчивается. Далее рассматриваем другой вариант управления, с которым осуществляются те же операции, и т. д. Просмотрев результаты исследо- [c.61]
Как уже говорилось, большинство математических моделей производственно-технологического уровня экономических систем содержат управляющие переменные, отражающие возможные воздействия на изучаемую систему. В связи с этим в зависимости от конкретных величин управлений реализуются различные варианты развития изучаемой системы. Так, например, выбирая в модели народного хозяйства различные допустимые (т. е. удовлетворяющие ограничениям (7.1)) управления st(i) п s2(t), получаем различные траектории системы — различные функции времени Kit), A(t), Y(t) и (t). Заказчик не может рассмотреть бесконечное число возможных вариантов развития системы, ему удается пред- [c.148]
Начнем с имитационных методов, как наиболее простых с концептуальной точки зрения. Как мы уже говорили в 4 гл. 1, в имитационных экспериментах задаются внешние воздействия на модель и рассчитываются последствия этих воздействий. В динамических системах внешние воздействия часто задаются как функции времени. Так, в модели народного хозяйства для всех значений t зададим управления st(t) и sz(f), удовлетворяющие ограничениям (7.1). Тогда по начальным состояниям системы К и АО можно построить траектории ее развития K(t) и A(t). При этом удается описать динамику показателей Y(t) и U). Сформулировав несколько вариантов управлений, можно построить различные траектории развития системы и значения показателей [c.149]
Самое серьезное внимание в зарубежной практике горизонтального бурения уделяется контролю и управлению траекторией ствола скважины, а также проведению измерений и записи всех технологических параметров бурения. [c.96]
Развитие наклонно направленного и горизонтального бурения потребовало разработки и применения надежной "навигационной системы", т.е. системы контроля за искривлением скважины и управления траекторией ствола (долота) при бурении. Такая система, включающая группу двигателя ("мотор") винтового типа (как вариант) и систему MWD (измерения в процессе бурения), была создана специалистами нескольких фирм, объединивших свои усилия в течение ряда лет, причем на реализацию идеи было истрачено примерно 1 млрд. дол. [c.96]
Помимо этого предусматривается прогнозирование фактического профиля до момента окончания набора кривизны по каждым пяти последним замерам координат забоя, и оперативного решения целого ряда частных задач по вопросам управления траекторией ствола скважины. [c.174]
В этом случае естественной задачей управления предприятием является недопущение предкризисного состояния и тем более его банкротства. Однако в силу динамичности развития хозяйственной среды и непредсказуемости наступления тех или иных событий, обусловливаемых самой сущностью рыночной системы хозяйствования, сложившаяся организационно-производственная и сбытовая модель развития предприятия может прийти в противоречие со складывающимися условиями хозяйствования. Этими условиями могут быть появление новых каналов распределения, новых технологий, конкурентов с новыми стратегиями или с товарами, позволяющими выступать с весьма привлекательными для потребителей предложениями. Все это в конечном итоге ставит перед управлением предприятия проблему его перевода на новую траекторию развития. [c.730]
Разработкой мероприятий по переводу предприятия в новую траекторию развития, выхода его из предкризисного и кризисного состояния занимается антикризисное управление. Понятие антикризисное управление — сложная экономическая категория. Эта сложность обусловливается тем, что в условиях предкризисного и кризисного состояния антикризисное управление осуществляется в рамках общепринятого управления, но с превалированием методов управления, нацеленных на выход из создавшегося кризисного состояния, а в условиях банкротства оно работает в системах санации и внешнего управления. Его методы отличны [c.731]
При автоматизированном управлении предприятием выполняется несколько основных фаз управления (рис. 7.2), позволяющих выдерживать сформулированную в общей математической модели управления (ОММУ) траекторию достижения цели - производства запланированной продукции [38]. [c.267]
Несмотря на упрощенный вид математической модели, ее результат может быть использован для укрупненного анализа национальной экономики. Параметры а и Ъ могут стать параметрами управления при выборе плановой стратегии развития с целью максимального приближения к предпочтительной траектории изменения национального дохода или для выбора минимального интервала времени достижения заданного уровня национального дохода. [c.107]
Наличие возмущений, воздействующих на производственный процесс, приводит к отклонению параметров, характеризующих реализацию производственной программы НПП, от показателей календарного плана. Поэтому в блоке коррекции проводится сравнение фактической и оптимальной траектории движения объекта управления. Отклонения в ходе реализации производственной программы могут быть обусловлены 1) малыми возмущениями, медленно меняющими параметры производственного процесса 2) существенными возмущениями, образующимися в результате накопления незначительных изменений технологических характеристик производства, которые своевременно не удалось скомпенсировать на нижнем уровне управления 3) значительными возмущениями, связанными, например, с изменением уровней отгрузки продукции, поступления сырья, изменениями состояния оборудования и т. п. [c.76]
Существуют, конечно, и другие причины для перехода к стратегии пассивного управления очень высокая концентрация активов, временное непонимание динамики различных секторов рынка и акцент на общерыночный уровень, а не на доходность отдельных ценных бумаг. Программы страхования портфелей, к примеру, сконструированы так, что они более эффективны для индексных портфелей, которые точно повторяют траекторию фьючерсных контрактов. Опционы, выписываемые на портфель акций, также работают лучше, когда менеджер может сосредоточиться на достойной оценке опциона, а не на оценке подпирающих его акций. Сторонники индексирования международных пакетов акций приводят еще один аргумент во многих странах финансовая отчетность не позволяет использовать основную технику анализа. [c.525]
ДИФФЕРЕНЦИАЛЬНЫЕ ИГРЫ [differential games] — игры, в которых в отличие от других игр стратегии выбираются по ходу игры и выигрьпи каждого участника зависит от траекторий управления, принятых всеми участниками игры. Число ходов и вместе с ними стратегий может быть бесконечным. [c.90]
ТРАЕКТОРИЯ УПРАВЛЕНИЯ [ ontrol traje tory] в задачах динамического программирования — совокупность значений вектора управляющих параметров, выбираемых на каждом этапе (шаге, фазе) оптимизации. См. также Фазовая траектория, Фазовое пространство. [c.365]
Траектория максимального сбалансированного роста 177 Траектория управления 365 Траекторные цели плана 386 Транзитивность предпочтений 365 Транзитология 365, 401 Трансакционная функция цены 387 Трансакционные издержки 366 Трансакционные мотивы спроса 142 "Трансакционные мотивы" спроса на [c.492]
Задача стохастического управления рассматривается как одноэтап-ная задача стохастического программирования, если описываемая моделью ситуация требует выбора закона управления для всей траектории системы (/ = 0, 1,. .., s—1) в один прием и коррекции по ходу управления в процессе накопления информации не допускаются. Априорные решающие правила определяют закон управления, зависящий только от детерминированных параметров и статистических характеристик случайных параметров условий задачи. Закон управления, определяемый апостериорными решающими правилами, зависит, кроме того, от реализации случайных исходных данных. Закон управления, соответствующий решающим распределениям, представляет собой случайный механизм формирования решения со статистическими характеристиками, зависящими (при апостериорных решающих распределениях) или не зависящими (при априорных решающих распределениях) от реализации случайных параметров условий задачи. Механизм управления, отвечающий решающим распределениям, может при одних и тех же реализациях исходных данных приводить к различным траекториям управления и, [c.45]
Если управление u(f), t0 / t2, переводящее систему из положения х(/о) в положение x(t0), является оптимальным, то в соответствии с принципом Л.С. Понтрягина1 фазовая траектория оптимального управления на отрезке ta t t2 должна соответствовать оптимальной кумуляте достижения цели ab . Так как уровни достижения локальных целей по содержанию и объему решаемых задач строго фиксированы (например, выражают сметную стоимость отдельных этапов работ возводимого сооружения), то существование на отрезке t0 t t2 некоторого управления v(t), переводящего систему из положения а в положение с по фазовой траектории аЬ2с, приводит к отклонению во времени момента свершения события Ъ (из Ъ в Ь2) на величину Д/. Но отклонение фазовой траектории управления системой от оптимальной кумуляты достижения цели означает, что управление v(t) не соответствует оптимальному. А несовпадение во времени моментов свершения события b свидетельствует о несогласованности на отрезке /0 = = h, т.е. указывает на несоответствие фактического производственного ритма оптимальному. [c.194]
Как только в 1946 году была построена первая в мире универсальная ЭВМ ЕМ1АС, компьютеры быстро доказали свое превосходство над людьми в скорости и точности вычислений во множестве сфер применения, справляясь как с управлением записями о клиентах крупнейших учреждений, так и с автоматизацией практически любых технических процессов, которые могут быть разложены на дискретные, многократно повторяющиеся шаги. Однако высшие сферы были компьютерам недоступны. Они помогали людям, но эту помощь трудно было назвать интеллектуальной. Для того чтобы понять физику процессов и разработать подробные программы вычисления траекторий артиллерийских снарядов или баллистических ракет, требуется человеческий мозг — и лишь затем для мгновенного выполнения этих вычислений в дело вступает гениальный тупица — компьютер. [c.33]
Медленный темп массового перехода к бурению долотами уменьшенных диаметров в наклонных скважинах по сравеннию с вертикальными скважинами отчасти объясняется трудностями управления траекторией ствола, вызванными уменьшением диаметра скважины, бурильного инструмента, забойного двигателя, поро-доразрушающего инструмента и т. д. Вместе с тем это указывает на наличие большого резерва в повышении эффективности проходки наклонных скважин. На практике долотами диаметром 269 мм бурят в одинаковых условиях и под промежуточную колонну — 219-мм хвостовик и под эксплуатационные 168 и 146-мм колонны. Если использование 269-мм долота под 219-мм хвостовик является рациональным, то его применение под указанные эксплуатационные колонны не может считаться таковым, так как приводит к утяжелению конструкции скважин, излишним затратам материалов, связанным с диаметром скважины, а также работ по разрушению пород, приготовлению, химической обработке и утяжелению раствора и т. д. [c.119]
Усиление контроля за ходом реализации планов на современном этапе практически означает последовательный переход от пассивной, формально-статистической фиксации расхождений между плановыми и отчетными показателями к активному воздействию на ход выполнения плана, с тем чтобы непрерывно направлять развитие экономики в плановое русло, минимизируя возможные (вызванные иногда объективными обстоятельствами) отклонения. Осуществление столь сложной задачи требует глубокого анализа функционирования экономики, своевременного выявления проявляющихся позитивных и негативных тенденций, расчета на основе соответствующих прогнозных моделей потенциально возможных отклонений от траектории планового развития народного хозяйства. Опираясь на эту научно-аналитическую работу и знание фактического положения дел на местах, плановые органы смогут обеспечить выработку эффективных рекомендаций о конкретных способах и путях воздействия на ход экономических процессов с целью приведения их в соответствие с плановыми. Преобразование системы контроля за выполнением плана в указанном выше направлении имеет очень важное, принципиальное значение в общем комплексе мер по совершенствованию планирования, повышению его действенности и эффективности. Большую роль в этом деле призваны сыграть также принятые в 1981 г. директивными органами меры по повышению роли Госплана СССР в системе государственного управления, по включению в соста этого комитета руководителей ряда центральных органи. заций, приданию ему ряда законодательных функций возрождению института Уполномоченных Госплан СССР по важнейшим экономическим районам Востокг страны. [c.22]
Техника, технологические процессы, ЧМС и комплексы с позиции выявления требований, которые они предъявляют к свойствам человека, изучаются рядом наук. Так, соответствие размеров тела человека, его моторных и других органов конструкции рабочего места, рычагам управления и т. д. исследуется современной антропометрией [16]. Двигательная сфера, величины нагрузки на отдельные группы мышц, усилия, траектории, скорости и количество движений составляют основной объект современной биомеханики. Сложный чувственно-двигательный (сенсомоторный) комплекс исследуется современной психофизиологией [45] и т. д. [c.12]
По полученным данным строится кривая местонахождения помощников бурильщика на разных стадиях (в разное время, при разных состояниях ЧМС) функционирования биотехнических систем — спуск бурильного инструмента и подъем бурильного инструмента. Траектория местонахождения первого помощника бурильщика, движение бурильного инструмента, элеватора и штропа в разное время при выполнении операций подъем и спуск бурильного инструмента показаны на рис. 41, из которого видно, что за время спуска одной свечи бурильщик проходит относительно большой путь по очень сложной траектории. В исследованиях нами показано, что вид кривой движения бурильщика на разных стадиях выполнения производственной операции характеризует сложность его двигательных действий по управлению (направлению, поддержанию) перемещаемым грузом (свечой, элеватором). По значению массы оператора и траектории перемещаемого груза были вычислены энергозатраты операторов при разном состоянии переносимого груза и исследуемой ЧМС. [c.166]
Проект создания ведомственной СУР НИД является комплексным по решаемым задачам и системным по структуре и составу участвующих административных и коллегиальных органов управления научной и инновационной деятельностью Минобразования России. Его реализация требует поэтапной разработки и внедрения отдельных элементов (модулей) СУР НИД. Учитывая имеющийся опыт взаимодействия и сложившиеся в научном блоке Минобразования России связи между научно-техническими и инновационными программами, целесообразно на первом этапе реализации ведомственной СУР НИД выбрать в качестве объекта управления научно-технический инновационный процесс с траекторией фундаментальные и поисковые НИР — прикладные и экспериментальные НИР — ОКТР — подготовка персонала, производства, материально-технической и технологической базы — выпуск и реализация наукоемкой продукции и оказание услуг (см. рис. 3). [c.14]
Сложность технологических процессов, многономенклатурность и многотоннажность современных нефтеперерабатывающих производств, динамичность условий их функционирования, случайный характер возмущений и неполнота информации о значениях параметров производственных процессов практически исключают возможность построения математической модели, адекватной объекту на большом интервале времени, и решения задачи по определению единой непрерывной оптимальной программной траектории. В связи с этим, как правило, осуществляется декомпозиция глобальной задачи управления нефтеперерабатывающими комплексами и предприятиями. [c.10]
Необходимо отметить, что в задачах планирования, в отличие от классических задач управления, не возникает необходимость определения непрерывной траектории функционирования. Приемлемая в практических ситуациях точность плановых расчетов обеспечивается кусочно-постоянной аппроксимацией непрерывных функций времени. При решении задачи календарного планирования нефтеперерабатывающих производств весь плановый период разбивается на ряд одинаковых временных отрезков, на каждом из которых решение представляет собойлибо постоянное по времени у-правление, либо среднюю или интегральную величину управляющих переменных. Точность и время решения задачи зависят от длительности этого отрезка времени. При прочих равных условиях его уменьшение ведет к повышению точности решения и снижению потерь оптимальности за счет повышения точности аппроксимации параметров модели. Одновременно происходит увеличение затрат времени на решение задач в связи с увеличением частоты ее решения. [c.77]
Таким образом, циклическая спиралевидная траектория изменений состояния предприятия есть результат непрерывного совокупного влияния разнонаправленных факторов внешней и внутренней среды его функционирования. Этим влиянием можно управлять на макро-, мезо- и микроуровне в процессе соответственно антикризисного регулирования экономикой страны, региона и антикризисного управления деятельностью предприятия. Множественность факторов, одновременно влияющих на деятельность предприятия, и их разнонаправленность свидетельствуют о сложности процессов антикризисного регулирования и антикризисного управления. Специалистам в этой области необходимо обладать широкой компетенцией относительно всесторонней деятельности предприятий. Схемы финансового оздоровления предприятий уникальны, однако классификация факторов, влияющих на их деятельность, позволяет типизировать антикризисный менеджмент. [c.45]
