Пределы Qin, 0-ia определяются исходя из функций распределений соответствующих переменных. Бри законах распределений с ограниченными диапазонами изменения переменных они определяются однозначно. Для законов распределений, имеющих асимптотический характер эти пределы задаются исходя из практически удовлетворительной точности вычислений. Так, для нормального распределения по "правилу трех сигм" можно принять следующие пределы [c.31]
Нормальный закон распределения имеет две формы представления плотность распределения (рис. 8.1 а) и функцию распределения (рис. 8.1 б). [c.117]
Временной ряд измерений дебитов Q. скважины при естественном снижении дебита представляется как сумма значений медленно изменяющейся функций Q(t.) и случайной составляющей с нормальным законом распределения и нулевым средним (МК]=0) [c.128]
Принимаем, что плотность распределения смешанных случайных величин стремится к нормальному закону распределения. Предельную точку кривой нормального распределения выражаем через функцию Лапласа [c.91]
Построение суммарной кривой распределения D производится весьма просто, если функции N и Ф подчиняются нормальному закону распределения или мало от него отличаются. В этом случае, как доказывается в теории вероятностей, кривая распределения D будет также нормальной кривой. [c.81]
Для проверки гипотезы о нормальном законе распределения оценки энтропии ff(X) при любом исходном распределении н.с.в. были проведены аналогичные эксперименты для случайных величин, генерируемых по следующим функциям [c.23]
Интегралы в этом выражении не могут быть выражены через элементарные функции. Более того, для интегральной функции нормального закона распределения нет ни таблиц, ни графиков, так как с их помощью невозможно охватить все многообразие возможных значений Q и а2 . Произведем поэтому замену переменной [c.76]
| Рис. 26. Дифференциальная (а) и интегральная (б) функции нормированного нормального закона распределения вероятности | 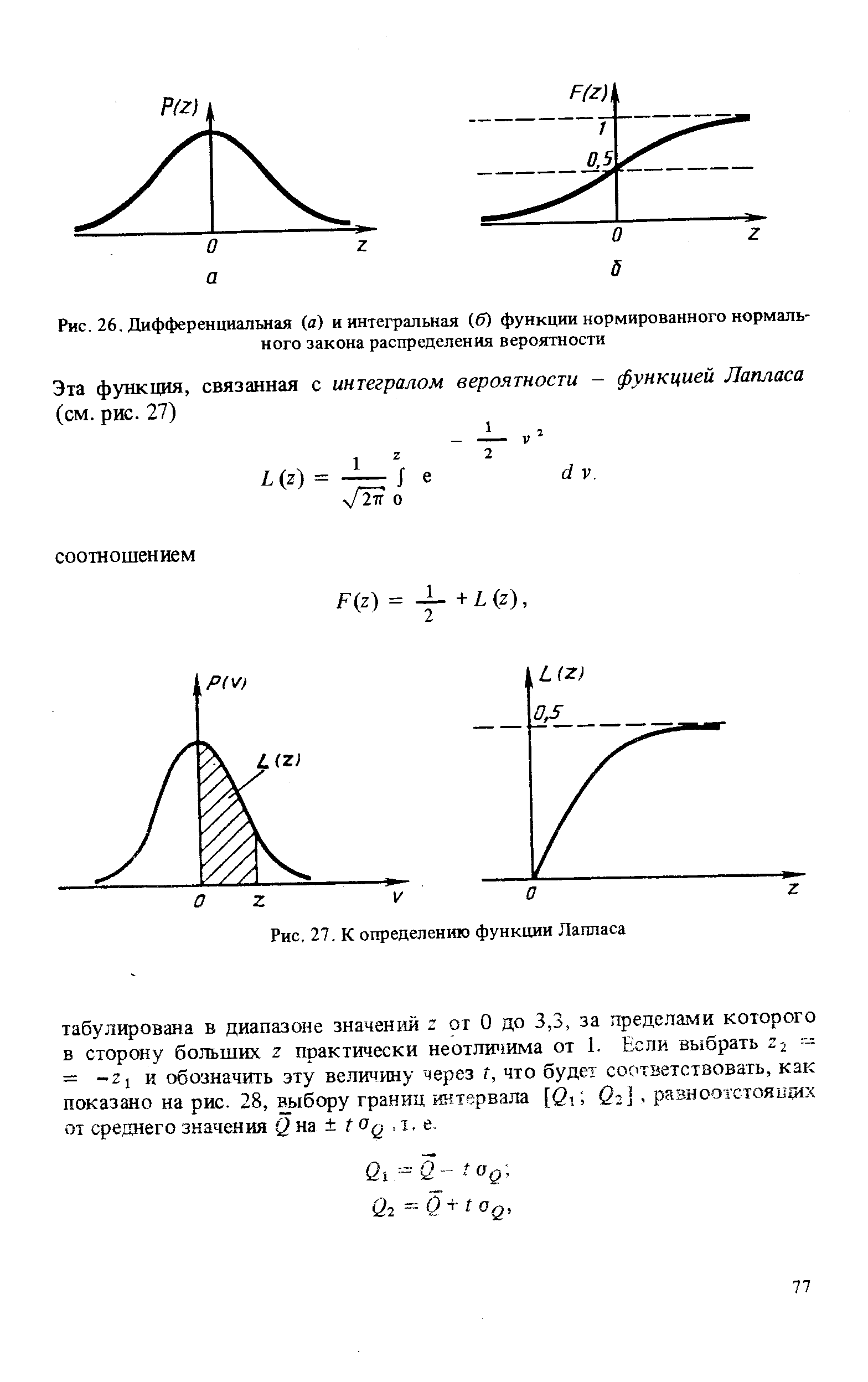 |
В предыдущей главе (см. п. 5.1) уже упоминалось, что если анализируемые переменные ( (1), (2),. .., (/7) т]) подчиняются (р + 1)-мерному нормальному закону распределения, то истинная функция / (X) регрессии т] по (1),..., (/7) принадлежит классу линейных (по x(k k = 1,2,..., р) функций (6.4). Однако статистическая проверка многомерной нормальности изучаемой векторной случайной величины относится к задачам, до сих пор плохо оснащенным достаточно эффективным инструментарием для их решения (см. сноску к с. 152 [14]). К тому же возможны ситуации, когда анализируемый многомерный признак (Ц1),..., < >> т]) не является нормальным, но в то же время регрессия г по ( (1),..., (р)) линейна. [c.180]
Значения функции плотности ф( ) = нормального закона распределения [c.437]
Центральная предельная теорема в какой-то степени оправдывает столь частое использование в экономике нормального закона распределения для аппроксимации функций распределения случайных величин, предположительно являющихся суммой большого количества независимых случайных величин. [c.110]
Для оценки вероятности отсутствия дефицита допустим, что отклонения ежедневного расхода деталей от среднего значения (тренда) подчиняются нормальному закону распределения. Тогда, воспользовавшись уравнением функции нормального закона, определим вероятность отсутствия дефицита по формуле [c.168]
Значения функции стандартного нормального закона распределения табулированы и приведены в приложении 6. [c.30]
Утверждение (Ь) является простым следствием того, что при нормальном законе распределения различных страт по величине a = E(ln ) (т.е. при условии, что смешивающая функция д(а) описывается (ад А2) — нормальной плотностью) смесь нормальных распределений логарифмов доходов вида [c.19]
Количественные характеристики портфеля ценных бумаг принято[8,9] рассматривать, исходя из предположений, что случайные величины, определяющие его эффективность, являются элементами генеральной совокупности с нормальным законом распределения. В терминах теории случайных функций [26] это эквивалентно понятию нормального стационарного случайного процесса (случайной последовательности). [c.125]
Докажите, что "Ft (х) > F2 (л ) верно для всех х", если закон распределения функций нормальный с Щ. < Ш и ai al или экспоненциальный с Е (jej) < (j 2). [c.262]
Основное преимущество метода Монте-Карло состоит в том, что можно рассмотреть все наиболее вероятные варианты последствий (исходов) оцениваемого проекта, правда, при существенных (ограничивающих область его применения) гипотезах и допущениях, главными из которых являются гипотеза о нормальном законе распределения, точнее, функции плотности (так называемого профиля каждого фактора, в частности профиля доходности инвестиций), знание математических ожиданий и дисперсий оцениваемых параметров (инвестиции, издержки, объем продаж, цена продукта и т.п.), возможность многократной (несколько тысяч раз) генерации на ЭВМ случайных исходов параметров в соответствии с принятой функцией распределения. Однако применение метода Монте-Карло не дает возможности (не только из-за "проклятия размерности") построить такую модель, которая учитывала бы все "весомые" факторы риска и тем более факторы неопределенности, а также реальные взаимосвязи и взаимозависимости реального проекта. [c.500]
Расчет вероятности наступления завершающего события в заданный срок обычно совершенно необходим, когда установленный директивный срок Гд оказывается меньше рассчитанного срока наступления завершающего события Тс. Предполагая, что значение 7"с подчиняется закону нормального распределения, можно рассчитать эту вероятность следующим образом. Аргумент нормальной функции распределения вероятностей (функции Лапласа) [c.235]
При построении регрессионных зависимостей вид кумулятивной функции распределения F(x) не носит принципиального характера, хотя как известно [90], ввиду используемого в этом случае метода наименьших квадратов полученные оценки наилучшим образом соответствуют нормальному закону распределения. [c.155]
| Рис. 3. Функция распределения нормального закона. | 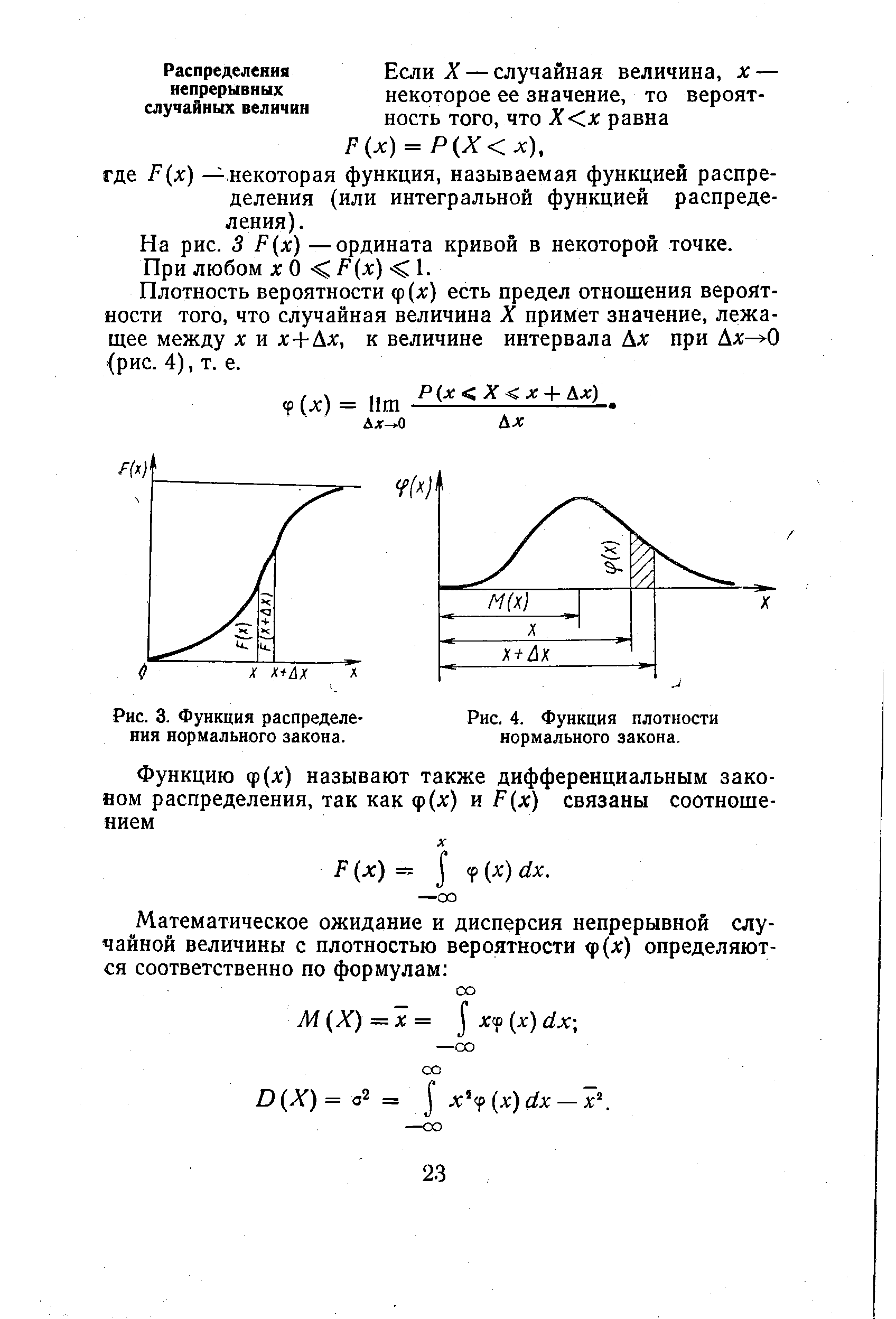 |
И наконец, следует уточнить, в соответствии с каким именно критерием качества аппроксимации неизвестных величин среднедушевых семейных денежных сбережений у (к) и уср (x) с помощью функции В0 + BI мы будем определять наилучший способ прогноза ср (х) по х. Наиболее обоснованное и точное решение этого вопроса опирается на знание вероятностной природы (а именно типа закона распределения вероятностей) остатков е в модели (В.З). Так, например, известно [14, с. 281], что если предположить, что при любых значениях к распределение вероятностей остатков е описывается (0, а2)-нормальным законом (т. е. нормальным законом со средним значением, равным нулю, и с некоторой, вообще говоря, неизвестной, но постоянной, т. е. не зависящей от х дисперсией а2) и что остатки е (дсг-), i = 1, 2,. .., п, характеризующие различные наблюдения, статистически независимы, то наименьшая ошибка прогноза (/ср (х) с помощью модели / (х) F (т. е. функция / (х) подбирается из класса F) обеспечивается требованием метода наименьших квадратов [c.17]
Функции потерь, имеющие горизонтальную асимптоту. Предложены три семейства функций, специально рассчитанных на асимметричные отклонения функции распределения ошибок от нормального закона. В унифицированных обозначениях в условиях, когда дисперсия основной (незасоренной) части распределения регрессионных остатков известна и равна единице, они могут быть приведены к виду (ниже параметр К > 0) [c.216]
В случае когда распределение е (в общем случае не обязательно симметричное) сравнительно мало отличается от нормального закона N (... 1), для всех трех функций рл, рм> [c.217]
Вторую группу составляют методы, использующие полную информацию о системе, т. е. о строении ее уравнений и о степени их стохастической зависимости. Наиболее известными представителями этой группы являются трехшаговый метод наименьших квадратов, рассмотренный в 14.4.3, и метод максимального правдоподобия. Между оценками, получаемыми при помощи этих методов, существует тесная взаимосвязь 3 мнк-оценки можно рассматривать в качестве первого приближения оценок метода максимума правдоподобия, по определению минимизирующих функцию плотности распределения наблюдений (в предположении, что они распределены по нормальному закону). Более того, указанные оценки асимптотически эквивалентны. [c.423]
Пример. Требуется определить значение функции распределения Ф ( а о) нормального закона в точке х = 3,36 при среднем а = 1 и среднеквадратическом отклонении о = 2. [c.438]
Влияние 7/ на область допустимых решений при нормальном законе распределения случайных величин может оыть в определенной мере оценено на основании приведенных в табл. 3.1 значений обратной функции нормального распределения. [c.93]
В случае распределения ЛГпо нормальному закону с функцией плотности Дх) = (1/л/2лё) е 2 энтропия h(x) равна [c.20]
По значению t/ из графика на рис. 29 можно опред пить, с какой вероятностью отдельное значение результата измерения, подчиняющегося нормальному закону распределения вероятности, попадает в интервал V100 Uj. С вероятностью в два раза меньшей оно попадает в левую или правую половину этого интервала. Эта вероятность, как показано в разд. 3.3.4, определяется интегралом вероятности - функцией Лапласа L (tj), так что для повышения точности расчетов можно пользоваться не графиком, а таблицами функции Лапласа. Полученные из таблиц значения /. (т/) занесены в пятую графу табл. 11. [c.108]
В качестве примера можно рассмотреть нормальный закон распределения с нечетким среднеквадратическим отклонением (рис. 2.6). Эта нечеткая функция не имеет полосового вида. И тут замое время заметить, что функция с треугольными нечеткими параметрами в общем случае сама не является треугольной и к треугольному виду не приводится. [c.37]
Интегрируя двумерную функцию плотности вероятности вектора скорости ветра в каждой точке рассматриваемой области по направлению 0 < <р 360 и модулю скорости О и икр, найдем функцию распределения превышения ПДК. В качестве теоретической функции плотности вероятности могут выступать, например, нормальный закон, приближение Лапласа-Шарлье, закон Вейбулла и др. Конкретный выбор зависит от степени близости к эмпирическому закону распределения, найденному по многолетним климатическим наблюдениям на метеорологических постах данной местности. Таким образом, мы выделяем зоны, в которых за интересующий интервал времени будут нарушаться установленные нормы загрязнения, получая новую характеристику — частоту превышения ПДК. Одновременно в каждой точке расчетной области имеем усредненную по всем реализациям среднюю концентрацию примеси. Необходимо отметить, что в аналитических решениях ось абсцисс совпадает с направлением среднего ветра, поэтому расчет загрязнения в каждой точке проводится во вращающейся полярной системе координат. При таком подходе многие недостатки аналитических решений, возникающие из-за упрощений исходных дифференциальных уравнений, нивелируются. [c.121]
Тинтнер предлагает для задачи стохастического программирования со случайной матрицей Л с независимыми нормально распределенными элементами и детерминированными векторами бис следующий приближенный метод вычисления Q(L ). Составим матрицу Аг=А+фоА, где элементы ац матрицы А — математические ожидания элементов оц матрицы А, а элементы матрицы СТА — среднеквадратические отклонения элементов йц от ац. Решим детерминированные задачи линейного программирования с матрицей условий At для ряда значений параметра t — реализаций некоторой случайной величины с заданной функцией распределения. Рассматривая полученные при этом оптимальные значения L t как случайную выборку, можно, используя соответствующие методы математической статистики, получить и оценить приближенное значение для (Ь ). Полученный таким образом закон распределения оптимального значения линейной формы для рассмотренного выше (см. п. 4.5) численного примера практически не отличается от функции Q(L ), изображенной на рис. 13.1. [c.299]
| Рис. 61. Равномерная плотность распределения вероятности результата измерения (7) и плотность распределения вероятности композиции двух (2) и трех (3) таких законов распределения вероятности (а - при Q = 0 б - при Q = 0,5) размахом является трапецеидальный закон. Это обстоятельство часто используется при учете дефицита информации. Рассматривая произведение большого числа характеристических функций, можно убедиться в том, что независимо от пида сомножителей оно стремится к характеристической функции, соответствующей нормальному закону распределения вероятности. Это фундаментальное положение носит название центральной предельной теоремы. На рис. 61 видно, как быстро нормализуется композиция одинаковых равномерных законов распределения вероятности. При числе слагаемых больше 4-х уже можно считать, что она практически подчиняется нормальному закону. | 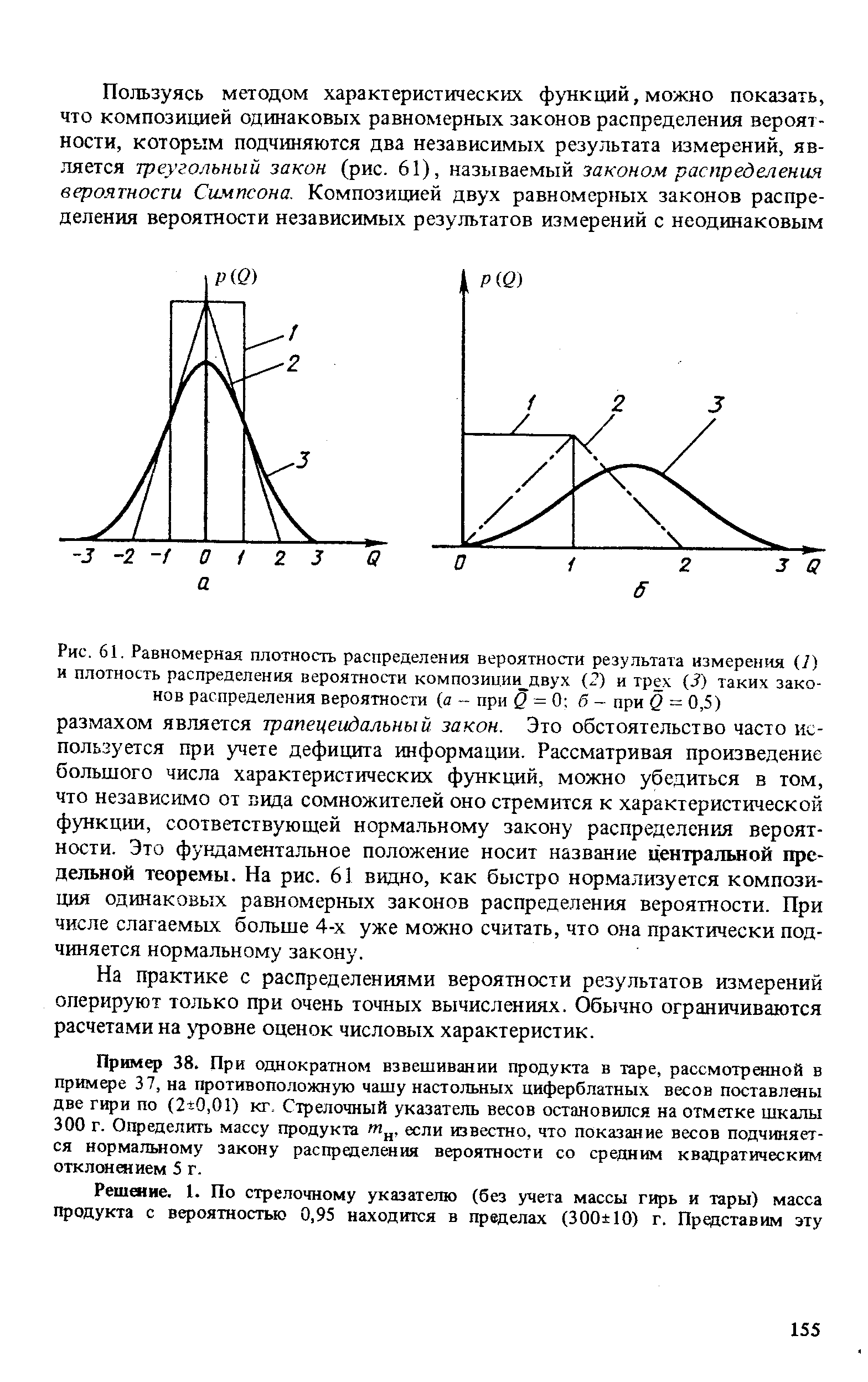 |
