Моделирование нормального распределения [c.55]
Из требования прибыльности разработки должно выполняться неравенство ZnK > a/ o + Р/Л/СО> которое следует из изложенных предпосылок. Оно определяет допустимые значения и соотношения констант при моделировании. Моделирование заключалось в реализации усеченной нормально распределенной случайной величины (запасов руды) VH с математическим ожиданием V и дисперсией о> и последующим расчетом всех величин, характеризующих отработку . [c.79]
Ещ г одним примером подобной абстракции является обоснование возможности использования регрессионных моделей в экономическом и финансовом анализе. Принципы моделирования с помощью регрессионных зависимостей в теоретическом плане разработаны в рамках теории вероятностей и математической статистики в частности, там предполагается случайность выборки, независимость ее элементов, нормальность распределения и т.д. Эти условия на практике выполнены далеко не всегда. [c.62]
В предыдущих примерах мы рассматривали моделирование дискретных переменных. А теперь давайте рассмотрим ситуации, когда требуется смоделировать непрерывные переменные, в частности те, которые соответствуют нормальному распределению. [c.334]
Моделирование рынков. Можно смоделировать различные переменные, связанные с деятельностью торговых и производственных предприятий, в частности объем продаж, спрос, колебания числа клиентов, ценовые изменения, объем производства, производственный контроль качества и текучесть кадров. Эти переменные часто моделируются с учетом непредсказуемого элемента, который можно смоделировать с помощью случайных чисел. В этих случаях приемлемо моделирование переменных с нормальным распределением. [c.338]
I) На производственной линии табачной фабрики Кристофер Форд , расположенной в Батон-Руж (Луизиана), инспекцией по проверке качества было установлено, что вес партии из 200 сигарет нормально распределен со средним 100 г и среднеквадратическим отклонением 1.2 г. Партии из 200 сигарет, вес которых менее 98.5 г, бракуются и пускаются на переработку. Смоделируйте производство первых 20 партий из 200 сигарет и зафиксируйте, какие партии бракуются. Сколько партий забраковано при этом моделировании Проанализируйте другие стратегии по контролю за качеством, в частности выбраковка партий весом менее 99.5 г или более 101 г. Как это повлияет на количество брака Сравните ваши результаты с ожидаемым количеством брака по методу нормального распределения вероятностей, который мы описали ранее в этой книге. [c.342]
Нормальное распределение вероятности далеко не всегда является хорошей моделью распределения торговых прибылей и убытков. Более того, ни одно из распространенных распределений вероятности не является идеальной моделью. Поэтому мы должны сами создать функцию для моделирования распределения наших торговых прибылей и убытков. [c.121]
Еще раз повторим, что эксперименты методом Монте-Карло проводились для проверки истинности уравнения (5.7). Для нормально распределенной случайной переменной, дважды перемешанной, 7 000 значений Н были рассчитаны для 10 < п < 50. Моделирование было проведено для Т = 200, 500, 1 000 и 5 000. Результаты приведены в Таблице 5.3 [c.80]
Моделирование было повторено для 10 < п < 500, 10 <= п <= 1000 и 10 < п < 5000. В каждом случае Е(Н) соответствовало значению, предсказанному уравнением (5.6), и дисперсия приблизительно равна 1/Т. На основании результатов таблицы 5.1 мы можем сказать, что Е(Н) для IID случайных переменных может быть рассчитано из уравнения (5.6), с дисперсией 1/Т. На рисунке 5.5 показаны "нормализованные" распределения для различных значений Т. Как и ожидалось, они оказываются нормально распределенными. [c.80]
Мы отметили в гл. 2, что наиболее широко из распределений частот используется нормальное распределение, или распределение Гаусса. Отсюда вытекает то обстоятельство, что наиболее широко используемым распределением вероятностей является нормальное распределение. Это распределение непрерывное, но часто применяется при моделировании дискретных случайных переменных. [c.191]
Нормальное распределение не является панацеей для всех проблем при моделировании. В частности, его использование при моделировании относительных цен активов может быть подвергнуто сомнению по крайней м,ере по двум причинам [c.210]
Симметричные распределения получаются при р = 0. Максимальное возможное значение а = 2, в этом случае получается нормальное распределение (для которого у = о2/2). Эмпирические свидетельства указывают на то, что подходящие значения а для моделирования распределения логарифмов доходностей меньше двух, возможны между 1,7 и 1,9, хотя такие распределения страдают недостатком — имеют бесконечно большую дисперсию [c.211]
Вместо использования нормального распределения при моделировании поведения цены, которое допускает ее отрицательные значения, можно моделировать натуральные логарифмы рентабельности как нормальное распределение. Это позволяет учесть го, что цена формируется в процессе умножения, а кроме того исключаются отрицательные значения. [c.218]
Утверждение (а) весьма распространено в исследованиях, посвященных моделированию распределительных отношений в обществе, и основан на мультипликативном характере воздействия на расход (доход, заработную плату) факторов в рамках населения однородной социально-экономической страты. Механизм генерирования логарифмически-нормального распределения в подобных ситуациях подробно описан в литературе (применительно, правда, к заработной плате, он был нами описан в (Айвазян С.А. и др., 1967)). [c.19]
Есть еще один уникальный метод статистического анализа, который известен под названием метода Монте-Карло. Он состоит в проведении множественных тестов на искусственных данных, сконструированных так, чтобы обладать свойствами выборок, извлеченных из случайной популяции. За исключением случайности, эти данные настроены так, чтобы иметь основные характеристики популяции, из которой брались реальные образцы и относительно которой требуется сделать заключение. Это весьма мощный инструмент красота моделирования по методу Монте-Карло состоит в том, что его можно провести, не нарушая основных положений статистического анализа (например, обеспечить нормальное распределение), что позволит избежать необоснованных выводов. [c.86]
Для моделирования распределений, возникающих при исследовании социально-экономических явлений, наиболее часто используется так называемое нормальное распределение. Известно, что закон нормального распределения характерен для распределения событий в случае, когда их исход представляет собой результат совместного воздействия большого количества независимых факторов и ни один из этих факторов не оказывает преобладающего влияния. В действительности нормальное распределение для экономических явлений в чистом виде встречается редко, однако если однородность совокупности соблюдена, фактические распределения можно считать близкими к нормальному. На практике для проверки обоснованности выбора того или иного типа распределения используются различные статистические критерии согласия (между эмпирическим и теоретическим распределением), которые позволяют принять или отвергнуть принятую гипотезу о законе распределения. [c.10]
Замечание. Представление (7.2), когда стартовая и финальная цены актива связаны экспоненциальным множителем, является неудобным для моделирования. Аналогичные неудобства вызывает представление доходности на основе степенной зависимости. Именно поэтому мы оперируем категорией текущей доходности как линейной функции дохода и финальной цены. Предполагая нормальность распределения финальной цены актива (что соответствует винеровскому описанию ценового процесса), мы автоматически таким образом приходим к нормальному распределению текущей доходности. Построенная линейная связь текущей доходности и цены является полезной особенностью, которая потом может быть удачно использована в ходе вероятностного моделирования. [c.99]
Полученные значения оценок параметров а и /3 в первой модели ( = -3.503812, / = 0.003254) соответствуют оценкам ft = 1076.77 и О" = 307.31 параметров функции нормального распределения, "сглаживающей" построенную ранее функцию Gn(x), график которой представляет ломаную. Заметим, что в действительности при моделировании данных мы использовали в качестве G(X) функцию нормального распределения с параметрами // = 1100 и (7 = 300. Следующий график позволяет сравнить поведение [c.22]
Моделирование нормального невырожденного многомерного распределения. ....... 61 [c.61]
Моделирование количества продуктивных пластов производится исходя из известной статистики по открытым в районе месторождениям (с использованием нормального закона распределения с математическим ожиданием и дисперсией, определяемыми из статистики). При реализации модели в нашем случае был использован упрощенный подход из реальной статистики количества продуктивных пластов в районе на каждом шаге имитации с равной вероятностью выбиралось количество продуктивных пластов. При более точном подходе необходимо -брать значения соответствующих геологических параметров в равномерно распределенных по площади района точках исходя из прогнозных карт. [c.203]
Проиллюстрируем использование метода Монте-Карло для определения стоимости одногодичного опциона на покупку актива, имеющего распределение дохода, изображенное на рис. 8.12. Текущая цена актива равна 1000 единиц, цена исполнения опциона также составляет 1000 единиц, а безрисковая процентная ставка равна 6% годовых (непрерывно наращенная). Мы используем технику моделирования, поскольку, как видно из рис. 8.12, эмпирическое распределение вероятностей не является нормальным. [c.418]
Нормальный закон - закон распределения случайных величин, имеющий симметричный вид (функция Гаусса). В имитационных моделях экономических процессов используется для моделирования сложных многоэтапных работ. [c.353]
Обобщенный закон Эрланга - закон распределения случайных величин, имеющий несимметричный вид. Занимает промежуточное положение между экспоненциальным и нормальным. В имитационных моделях экономических процессов используется для моделирования сложных групповых потоков заявок (требований, заказов). [c.353]
Примем, что время начала первого дня движения — 8 ч утра. Смоделируем первую составляющую — время движения Санкт-Петербург—Торфяновка. Согласно табл. 6.10, оно подчиняется нормальному закону распределения с параметрами х = 3,79, а= 0,7. Моделирование случайной величины tu производится по формуле, представленной в табл. 6.4. [c.142]
Для проверки непротиворечивости двух прогнозов можно использовать и другой метод [26, 63]. Полагая обе прогнозные оценки распределенными по нормальному закону, прогнозы можно считать непротиворечивыми, если выполнено неравенство t < tT3 Jl(p, v), где 1 1 — модуль расчетного критерия Стьюдента таб.,(р, v) — табличное значение критерия Стьюдента для р-го уровня надежности и числа степеней свободы п = N + N2- т - 2 (Л — число наблюдений динамического ряда, N2 — число экспертов). При такой оценке непротиворечивости прогнозов речь фактически идет об использовании методов определения принадлежности выборок к одной генеральной совокупности. Если прогнозные оценки получены по результатам моделирования, то данный критерий для оценки непротиворечивости прогнозов применяться не может. [c.206]
Моделирование нормально распределенной случайной величины может быть произведено по формуле, представленной в табл. 6.4 или с помощью встроенного в MS Ex el генератора случайных чисел. Например, для моделирования времени транспортировки необходимо задать (рис. 6.4) число переменных — 1 (каждая операция логистического цикла моделируется отдельно) число случайных чисел, например, — 50 распределение — нормальное параметры — среднее 4,5 и СКО — 1,31. Также необходимо задать выходной интервал. [c.133]
| Рис. 6.4. Моделирование нормально распределенной величины с помощью MS Ex el | 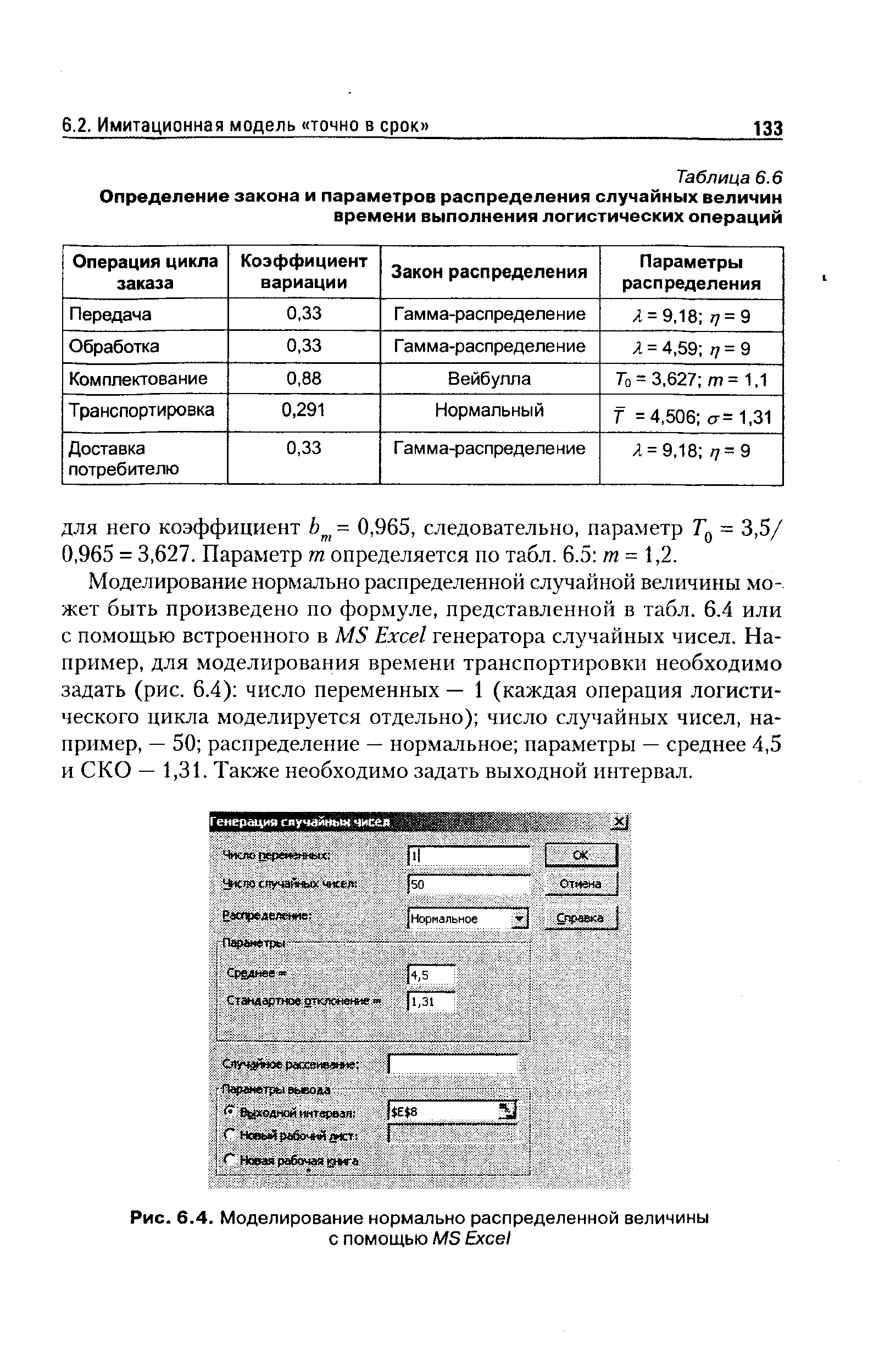 |
Моделирование случайных величин, распределенных с известными параметрами, по расчетным формулам табл. 6.4 производится с генерированием равномерно распределенных случайных чисел в интервале (0 1) или нормально распределенных случайных чисел , с параметрами среднее — 0, среднее квадратическое отклонение — 1. Если объем моделируемых величин невелик, то для получения случайных чисел и можно воспользоваться специальными таблицами. Получить и Ц можно также с помощью входящей в современное программное обеспечение стандартной процедуры формирования случайных чисел. В частности, производя расчеты в электронных таблицах MS Ex el, необходимо подключить надстройку Пакет анализа , после чего в падающем окне меню Сервис появится команда Анализ данных . В одноименном диалоговом окне необходимо выбрать такой инструмент анализа, как Генерация случайных чисел . [c.132]
В этом параграфе мы дадим обзор тех существующих ММР, которые, по нашему мнению, могут пригодиться в имитационных экспериментах. Поскольку наша главная забота—применимость в моделировании, будем классифицировать методы по предпосылкам, лежащим в их основе. Все методы предполагают независимость наблюдений (внутри и между совокупностями). Из параметрических методов возьмем только ММР для нормальных распределений. Мы предполагаем, что этот тип методов наиболее широко применим в имитационном моделировании по сравнению с другими параметрическими методами. Нормальное распределение служит адекватной аппроксимацией многих других распределений, и отклонения между действительным неизвестным распределением и нормальным предполагаются не столь уж страшными. Мы вернемся к проблеме робастности методов в следующем параграфе. Методы, основанные на других распределениях, кратко описаны в V.B.5. Здесь же мы изучим еще непараметрические или полунепараметрические ММР. Помимо различий параметрические—непараметрические между распределениями могут существовать и другие различия только в расположении или как в расположении, так и в форме. Для нормальных совокупностей последнее различие эквивалентно различию равные дисперсии — неравные дисперсии. Другая классификация известные дисперсии — неизвестные дисперсии. Все ММР из этого параграфа используют подход, основанный [c.221]
Помимо предположения о известных дисперсиях при имитационном моделировании может нарушаться также предположение о нормальности распределений. В приложении V.B.2 приведен метод, не требующий, чтобы наблюдения были нормальными, а удовлетворяющийся тем, что нормальны выборочные средние. В силу центральной предельной теоремы это довольно слабое предположение. (Следовательно, метод можно применять для ранжирования других параметров, кроме средних из нормальных совокупностей, при условии, что средние оценки этих параметров имеют приближенно нормальные распределения см. также [Be hhofer, 1954, р. 29].) Заметим, что оценки дисперсий для распределений с нарушением нормальности остаются несмещенными. [c.247]
Моделирование показывает, однако, что при умеренных значениях Т распределение статистики G 2 плохо приближается нормальным распределением. Более того, процедура проверки здесь весьма общая (структура временного ряда не специфицируется). Поэтому критерий нормальности, основанный на статистике [c.52]
Однозначно оценить коэффициенты в (2) не представляется возможным, поэтому необходимо сделать дополнительные предположения об их природе. Пусть а -случайная величина, реализующаяся для каждого региона и налога согласно нормальному распределению с ненулевым математическим ожиданием для каждого налога а, и фиксированной дисперсией а Также предположим, что /3 фиксированный вектор, одинаковый для всех территорий и во времени, но с разными элементами для каждого налога. Это равносильно утверждению, что все факторы, влияющие на /3 , в том числе и налоговые усилия территории, предполагаются одинаковыми для всех территорий и постоянными во времени. Такое упрощение ведет к снижению прогнозирующих возможностей модели, но позволяет обойтись без сложного моделирования зависимости /3 от налоговых усилий, разных для территорий внешних и случайных факторов. Отказ от данного упрощения потребует перехода кэконометрическим моделям на основе временных рядов, панельных данных или одномерному детерминистическому методу прогнозирования. [c.71]
Классический подход к моделированию риска исходит из нормального распределения доходности активов, или логарифмической нормальности цен. Классическая взаимосвязь между риском и доходностью представляется в двумерном пространстве среднее значение (доход) и дисперсия (риск). Если показатели дохода на активы дают нормальное многомерное распределение, то степень рискованности всего портфеля определяется лишь матрицей ковариации показателей дохода. Стоимость риска — это оценка максимального убытка, ожидаемого на протяжении определенного периода. Риск в этом случае измеряется величиной максимального убытка, оцениваемой с помошью исторического моделирования или [c.77]
IFPS поддерживает детерминистское и вероятностное моделирование и позволяет получать выборку, распределенную по различным законам равномерному, нормальному, двумерному нормальному и заданному пользователем закону эмпирического распределения [c.314]
Стоит начать с того, чтобы изобразить распределение переменной с помощью гистограммы или же рассчитать для него характеристики асимметрии (симметричность распределения) и эксцесса (весомости хвостов распределения). В результате будет получена информация о том, насколько распределение данных близко к нормальному. Многие методы моделирования, в том числе, — нейронные сети, дают лучшие результаты на нормализованных данных. Далее, с помощью специальных статистических тестов, например, на расстояние Махаланобиса, можно выявить многомерные выбросы, с которыми затем нужно разобраться на предмет достоверности соответствующих данных. Эти выбросы могут порождаться ошибочными данными или крайними значениями, вследствие чего структура связей между переменными может (а может и не) нарушаться (см. [19]). В некоторых приложениях выбросы могут нести положительную информацию, и их не следует автоматически отбрасывать. [c.61]
Жуленев С. В. Нормальная модель для задач со случайными ограничениями. Равномерное распределение. — В кн. Моделирование экономических процессов , МГУ, 1971, с. 403—414. [c.385]
Во 2-м томе К. Маркс исследует кругооборот и оборот капитала, а затем даёт анализ воспроизводства обществ, капитала, взятого в целом. Маркс раскрыл коренную ошибку представителей классич. школы бурж. нолптич. экономии, к-рые, начиная с А. Смита, утверждали, что стоимость обществ, продукта слагается из доходов заработной платы, прибыли и ренты. На самом же доле, как выяснено в К. , стоимость обществ, продукта распадается на стоимость потреблённых элементов постоянного капитала (средств нроиз-ва), стоимость переменного капитала (рабочую силу) и прибавочную стоимость. В соответствии с этим Маркс впервые в истории экономич. науки разделил всё обществ, произ-во на 2 подразделения I — произ-во средств произ-ва и II — произ-во предметов потребления. Условия реализации обществ, продукта при простом и расширенном капиталистич. воспроиз-ве Маркс раскрывает в схемах воспроиз-ва, применив впервые в истории метод исследования экономич. процессов, получивший впоследствии широкое распространение и известный под названием моделирования. Данный во 2-м томе К. анализ показывает, что ...условия нормального хода как простого воспроизводства, так и воспроизводства в расширенном масштабе,. ..превращаются в столь же многочисленные условия ненормального хода воспроизводства, в столь же многочисленные возможности кризисов, так как равновесие — при стихийном характере этого производства — само является случайностью (там же, т. 24, с. 563). Раскрыв трудности и противоречия капиталистич. реализации, Маркс приходит к выводу о неизбежности периодич. нарушений этого процесса. Сама многосложность процесса дает столь же многочисленные основания для его ненормального хода (там же, с. 564). В 3-м томе К. дан подробный анализ сложного механизма распределения прибавочной стоимости между отд. группами эксплуататоров. Закон средней нормы прибыли регулирует её распределение между непосредственными получателями прибавочной стоимости — пром. капиталистами. В процессе дальнейшего [c.100]
В V.A.3 мы приведем ряд хорошо известных результатов для доверительных интервалов и критериев для среднего одной нормальной совокупности или разности между средними двух нормальных совокупностей. Мы обсудим, например, /-критерий для одной либо двух совокупностей с неизвестными и возможно различными дисперсиями. Рассматриваются предположения -критерия и имитационное моделирование, а также биномиальное распределение и оценивание квантилей. В V.A.4 изучается определение объема выборки. Для доверительного интервала заданной длины обсуждается двойная выборка и (асимптотически состоятельная и эффективная) последовательная выборка. Многочисленные применения в моделировании и экспериментах Монте-Карло показывают, что правила останова срабатывают. Мы также определим объем выборки для проверки гипотез с заданными ошибками аир при применении двойной выборочной процедуры. В качестве альтернативы можно взять подход, основанный на селекции ( зона безразличия ), который отбирает с заданной надежностью уточненную совокупность. Эвристический последовательный метод применен в имитационном эксперименте. Проверку гипотез с заданными ошибками а и р и строго последовательной выборкой можно осуществить по критерию последовательного отношения вероятностей Вальда (Wald) (КПОВ) (при условии, что нет мешающих параметров следовательно, для биномиальной совокупности существует точный КПОВ). Часть А заканчивается приложениями, упражнениями и библиографией. [c.121]
Смотреть страницы где упоминается термин Моделирование нормального распределения
: [c.139] [c.99] [c.163] [c.29] [c.41] [c.146] [c.181] [c.245] [c.246]Смотреть главы в:
Моделирование и управление в экономике Часть 1 -> Моделирование нормального распределения
