Экстраполяция кривой регрессии 67 [c.306]
Предварительное, до подачи на вход сети, преобразование данных с помощью стандартных статистических приемов может существенно улучшить как параметры обучения (длительность, сложность), так и работу системы. Например, если входной ряд имеет отчетливый экспоненциальный вид, то после его логарифмирования получится более простой ряд, и если в нем имеются сложные зависимости высоких порядков, обнаружить их теперь будет гораздо легче. Очень часто ненормально распределенные данные предварительно подвергают нелинейному преобразованию исходный ряд значений переменной преобразуется некоторой функцией, и ряд, полученный на выходе, принимается за новую входную переменную. Типичные способы преобразования — возведение в степень, извлечение корня, взятие обратных величин, экспонент или логарифмов (см. [250]). Нужно проявить осторожность в отношении функций, которые определены не" всюду (например, логарифм отрицательных чисел не определен). После этого могут быть применены дополнительные преобразования для изменения формы кривой регрессии. Часто это на порядок уменьшает требования к обучению [284], [251]. [c.61]
Для оценки вероятности выживания фирмы мы можем использовать два способа. Во-первых, можно основываться на прошлом — рассмотреть фирмы, потерпевшие банкротство, и сравнить их с фирмами, которые этого избежали, а затем выявить переменные, различающие их. Например, фирмы с отрицательными долговыми коэффициентами и отрицательными денежными потоками от операций с большей вероятностью потерпят банкротство, чем фирмы, не обладающие этими свойствами. Кроме того, для оценки вероятности банкротства фирмы можно использовать статистические методы (например, пробиты, или кривые регрессии). Для выведения пробитое следует начать со всех зарегистрированных в 1990 г. фирм и их финансовых характеристик, а затем определить те фирмы, которые потерпели банкротство в период 1991-1999 гг., и оценить вероятность банкротства как функцию переменных, наблюдавшихся в 1990 г. Результат, напоминающий результат регрессии, позволит оценить вероятность дефолта для любой фирмы в настоящий момент времени. [c.423]
Критика Фридмена настолько сильно опровергает эмпирические результаты, что требуется дальнейшее изучение. Предположим, что мы пересмотрели затраты, чтобы исключить доходы, получаемые за счет факторов, специфичных для фирмы (например, за счет предпринимательских способностей), а затем вычислили регрессию этих затрат на выпуск продукции можно ли рассматривать результаты как некоторого рода среднее из кривых долгосрочных средних затрат отдельных фирм Действительно, кривая регрессии покажет нам, как с изменением продукции менялись предпринимательские способности. Это весьма ценный результат, но он не имеет тесной связи с кривой затрат отдельной фирмы. Конечно, подобные критические высказывания неприменимы к исследованиям фирм при монополистических условиях [52]. Но тогда самой важной становится проблема оценки затрат и активов. А если рассматривать дифференциацию продукции как причину различных объемов выпуска, тогда концепция кривой затрат становится совершенно неясной.19 Фридмен не уничтожил полностью метода анализа на множестве объектов, но нанес ему тяжелый удар. [c.187]
Оценка технико-экономического уровня продукции методом сравнительного анализа позволяет оценить не только технический уровень, но и уровень конкурентоспособности изделий. В РБ для этой цели создана автоматизированная система Бисер . Основные этапы анализа, проводимого в рамках этого метода, сводятся к следующему экспертным методом определяются параметры, коэффициенты их значимости и степень их влияния на цену для объекта сравнения выбираются аналоги. для сравнения на основе накопленных данных по совокупности параметров всех оцениваемых изделий находится зависимость между параметрами и строится кривая регрессии. Далее определяются теоретические значения цены и устанавливается степень отклонения каждого исследуемого объекта от этого уровня (по всем параметрам). Среди всех исследуемых параметров выделяется главный, и как функция каждого главного параметра определяется теоретическая (ориентировочная) цена изделия, а также технико-экономический уровень как соответствие между теоретической и действительной ценой, с одной стороны, и цены и техническим уровнем — с другой. [c.100]
Окончательный выбор аппроксимирующей кривой между уравнением регрессии, полученным на основе динамического ряда предложений ВНИИОЭНГ, и уравнением регрессии, полученным на основе динамического ряда фактических удельных расходов, по каждому материалу осуществлялся на основе сопоставления полученной величины прогноза с показателями, 1979 г. [c.25]
Простая регрессия — это функция с одной независимой переменной, которая выражается уравнением прямой, параболой второго и n-го порядка, гиперболой, уравнением показательной степенной кривой и т. д. [c.66]
Тип кривой выбирается на основе сочетания теоретического анализа и исследования исходных эмпирических данных. Теоретический анализ наряду с обычными логическими сопоставлениями известных научных понятий включает опыт предыдущих исследований, экспертные оценки специалистов. Эмпирический путь заключается в изучении имеющихся исходных данных посредством построения корреляционных полей и эмпирических линий регрессии, а также анализа параллельных рядов, в результате которого исследуются разности между парами значений признаков (увеличивающиеся и уменьшающиеся абсолютные разности, постоянные и изменяющиеся относительные роста и т.д.). Изучение эмпирического материала показывает наличие или отсутствие связи, ориентирует ее направление и форму. Так, если результативный признак по сравнению с факторным увеличивается с одинаковой скоростью — связь прямолинейная, одинаковым темпом — связь экспоненциальная и т.п. [c.320]
В практике экономических исследований имеющиеся данные не всегда можно считать выборкой из многомерной нормальной совокупности, когда одна из рассматриваемых переменных не является случайной или когда линия регрессии явно не прямая и т. п. В этих случаях пытаются определить кривую (поверхность), которая дает наилучшее (в смысле метода наименьших квадратов) приближение к исходным данным. Соответствующие методы приближения получили название регрессионного анализа. [c.50]
Индикатор прогноза временных рядов (TSF) показывает статистическую тенденцию цен за определенный период времени. Эта тенденция определяется на основе анализа линейной регрессии. В отличие от прямых линий тренда линейной регрессии (см. стр. 90), график индикатора TSF — это кривая, составленная из последних точек множественных линий тренда линейной регрессии. Поэтому индикатор TSF иногда называют индикатором скользящей линейной регрессии или регрессионным осциллятором . [c.168]
Кумулятивная кривая дохода сделок показывает изменение торгового счета от сделки к сделке. Для анализа поведения счета во времени используют сгруппированный отчет о величине торгового счета. Изучение поведения счета по укрупненным периодам времени полностью аналогично изучению кумулятивной кривой дохода сделок. Для той же механической системы на рисунке изображен логарифм эмпирической нормированной величины торгового счета на конец каждого квартала на периоде тестирования (у линейная аппроксимация ( f ) и 95%-ный доверительный интервал линии регрессии. Как правило, для анализа линии торгового счета выбираются месячные или квартальные данные. [c.197]
Для оценки способностей инвестиционного менеджера правильно выбирать время операции иногда бывает необходимо использовать более сложные зависимости, чем просто прямая линия, для аппроксимации точечных диаграмм, таких, как изображенные на рис. 25.7. Рассмотрим процедуру, которая позволяет построить соответствующую кривую, причем используются статистические методы оценки параметров a, b и с в следующем уравнении квадратичной регрессии [c.902]
В обеих регрессиях, описываемых уравнениями (25.24) и (25.26), значение параметра а представляет собой оценку возможностей менеджера по определению ценных бумаг с заниженной ценой (т.е. умение менеджера правильно выбрать ценные бумаги), а значение параметра с представляет собой оценку возможностей менеджера в области выбора времени операций. При этом квадратичное уравнение показывает, что бета портфеля принимала различные значения в зависимости от размера избыточной доходности рынка. Графически это выражается в том, что наклон квадратичной кривой постоянно увеличивается при движении слева направо на рис. 25.8(а). Уравнение модельных переменных, в свою очередь, показывает, что бета портфеля меняется в промежутке между двумя значениями гиг зависящими от величины rjf Графически это выражается в том, что наклон, задаваемый данным уравнением, возрастает от одного значения (Ь - с) до второго значения (Ь) при движении слева направо на рис. 25.8(6). [c.904]
При изучении зависимости между двумя признаками графический метод подбора вида уравнения регрессии достаточно нагляден. Он основан на поле корреляции. Основные типы кривых, используемые при количественной оценке связей, представлены на рис. 2.1. [c.37]
Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез. Как показывает опыт большинства исследователей, среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени в отдельных случаях — полином третьего порядка. Ограничения в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно менее однородна совокупность по результативному признаку. [c.63]
Н.р. унимодально (см. Мода), описывается колоколообразной (симметричной) кривой его средняя математическое ожидание) совпадает с модой (рис. Н.6). Н.р. чрезвычайно широко используется в математической статистике. В частности, в моделях регрессии часто ошибка принимается распределенной по этому закону. Предпосылка Н.р. учитывается и в большинстве критериев статистической проверки гипотез. Между тем в экономике Н.р. во многих случаях неприменимо напр., вряд ли можно представить себе цены, распределенные по нормальному закону, тогда в модель вошли бы также отрицательные цены. К тому же выборки в экономических исследованиях часто слишком малы (см. Неполная выборка). [c.229]
Метод наименьших квадратов и процедуры подбора прямой регрессии, описанные в предыдущей главе, полностью переносятся и на случай, когда уравнение кривой может быть после некоторых преобразований сведено к линейному тренду [c.87]
При этом просматриваются регрессии на линейных областях двойных логарифмических кривых. Фрактальная размерность должна в конце концов сходиться к своей истинной величине, по мере того как будет увеличиваться размерность вложения. [c.198]
На рис. 6.12 показан пример восстановления полинома пятой степени на отрезке [—2,2]. Восстановление проводилось по измерениям функции в 20 случайно взятых точках (крестики). Видно, что кривая 2 лучше приближает истинную регрессию, чем кривая /. [c.196]
При изучении литературы оказывается, что ошибка регрессии вызывает самую сильную критику метода анализа по множеству объектов. Спорят, что производимая (и продаваемая) каждой фирмой продукция обычно является случайной переменной и колебания выпускаемой продукции вокруг среднего значения не контролируются фирмой. Фирма определит наилучший способ распределения выпускаемой продукции. По словам Фридмена, если нет переменных затрат, то исследование на множестве объектов продемонстрирует резкое снижение средних затрат. Когда фирмы классифицируются по действительному выпуску продукции, тогда возникает именно такой тип смещения. Фирмы с наивысшими объемами выпуска вряд ли будут производить продукцию на непривычно низком уровне в среднем они явно скорее будут выпускать продукцию на необычно высоком уровне в отличие от тех, чей уровень выпуска является самым низким [39]. Эта критика была широко принята. Были предприняты попытки избежать ошибки регрессии путем классификации фирм по предприятиям и проверкой значимости внутризаводской и межзаводской регрессии [11]. С другой стороны, спорили, что если выпускаемая продукция является случайной переменной, то оценочной кривой затрат для принятия решения будет кривая ожидаемых затрат, а не кривая затрат, вызываемых случайными изменениями объемов выпуска [94]. Кривые ожидаемых затрат будут более пологими, чем исходные кривые. Поскольку учетный период обычно включает в себя много единичных экономических периодов, имеющиеся реально в наличии данные в основном будут приближаться к ожидаемому объему выпуска. Если данное положение справедливо, то это дает начало объяснению того, почему в оцененных кривых затрат наблюдается почти линейность и почему следует более серьезно воспринимать результаты этих исследований. [c.192]
Применение корреляционного анализа позволяет установить наличие или отсутствие связи между изучаемыми величинами в условиях действия большого числа факторов, ряд из которых неизвестен. Наличие или отсутствие связи определяется путем составления уравнений связи или, как их принято называть, уравнений регрессий. Форму связи (прямолинейную или криволинейную) определяют на основе предварительного анализа. О наличии корреляционной связи, а также о форме и характере кривой в первом приближении может дать представление графический анализ распределения совокупности точек, образующих корреляционное поле. Так, вытянутый характер расположения точек и ось контура корреляционного поля, составляющая острый или тупой угол с осями координат, свидетельствуют о наличии корреляционной связи и прямолинейной формы связи. Если наибольшая ось контура корреляционного поля параллельна одной из осей координат или контур поля приближается к форме круга, то такое соотношение исследуемых факторов не имеет или почти не имеет корреляционной связи. [c.114]
Для точного описания уравнения регрессии необходимо знать условный закон распределения зависимой переменной Y при условии, что переменная X примет значение дс, т. е. Х=х. В статистической практике такую информацию получить, как правило, не удается, так как обычно исследователь располагает лишь выборкой пар значений (х/, у,) ограниченного объема п. В этом случае речь может идти об оценке (приближенном выражении, аппроксимаций) по выборке функции регрессии. Такой оценкой1 является выборочная линия (кривая) регрессии [c.52]
| Рис. 15. Графики расположения точек па ноле корреляции при выборе и обосновании типа кривой регрессии а —линейная зависимость б—гипербола в—парабола пторого порядка г —парабола третьего порядка | 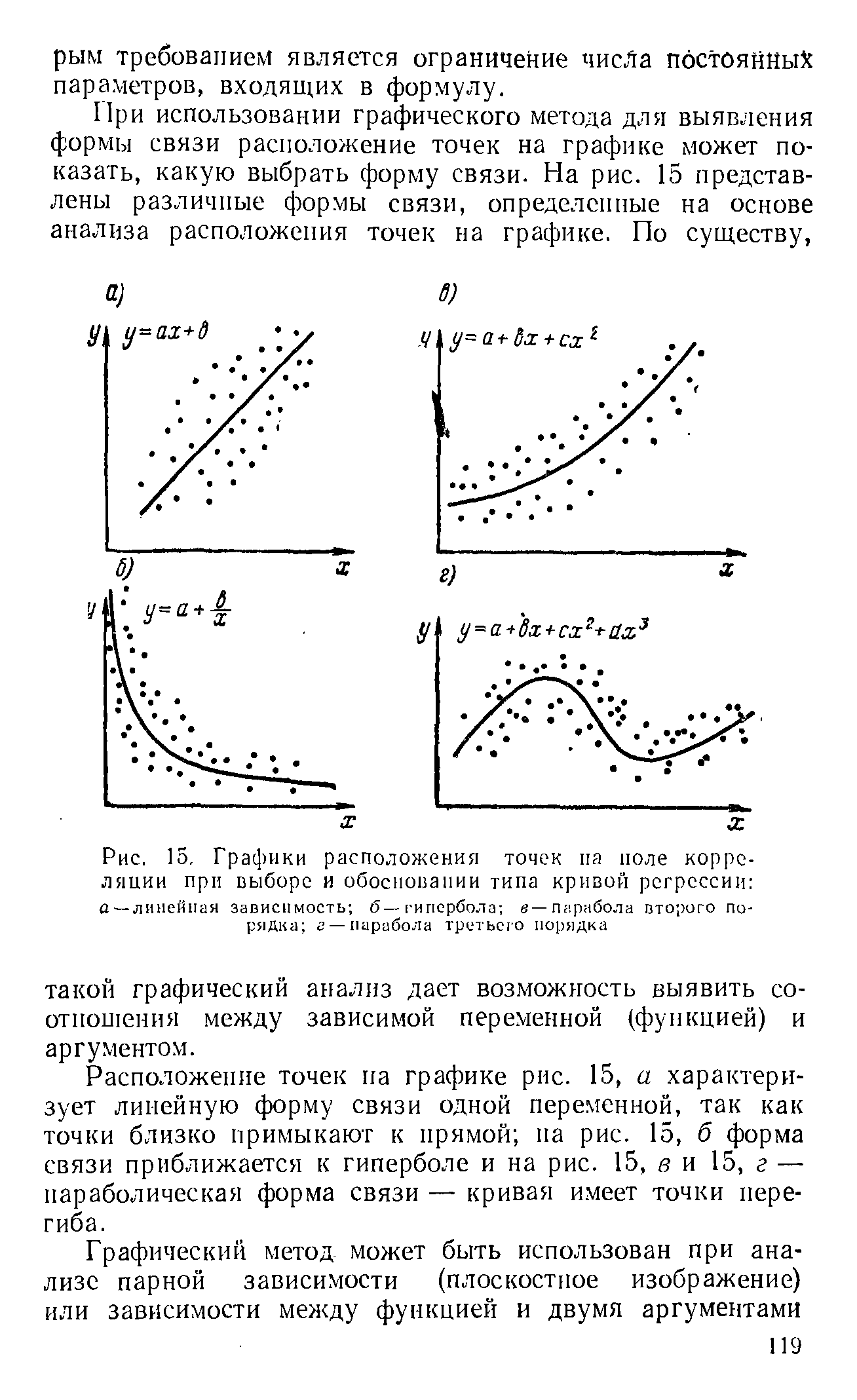 |
Математика-статистическое направление существует в трех вариантах. У Д. Р. Лонгмана — М.Шифа эта методология основана на построении коэффициентов корреляции между отдельными видами издержек и степенью занятости. У К. Руммеля коэффициенты корреляции рассчитываются между потреблением (издержками) и выпуском готовой продукции. У Вольтера кривые издержек построены на основе коэффициента регрессии. Бернер считал, что этот подход ничем не лучше предыдущего оба могут применяться только при наличии готовых данных, оба устремлены в прошлое и дают тем более точные результаты, чем длиннее промежуток времени, подвергшийся анализу. Тут мы можем сформулировать парадокс [c.226]
В ситуации, когда нет рычага (например, портфель акций без заемных средств), вес и количество одно и то же. Однако в ситуации с рычагом (например, портфель фьючерсных рыночных систем), вес и количество отличаются. Идея, которая была впервые изложена в книге Формулы управления портфелем , состоит в том, что мы пытаемся найти оптимальное количество, и оно является функцией оптимальных весов. Когда мы рассчитываем коэффициенты корреляции HPR двух рыночных систем с положительными арифметическими математическими ожиданиями, то чаще всего получаем положительные значения. Это происходит потому, что кривые баланса рыночных систем (совокупная текущая сумма дневных изменений баланса) стремятся вверх и вправо. Проблема решается следующим образом для каждой кривой баланса надо определить линию регрессии методом наименьших квадратов (до приведения к текущим ценам, если оно применяется) и рассчитать разность кривой баланса и ее линии регрессии в каждой точке. Затем следует преобразовать уже лишенную тренда кривую баланса в простые дневные изменения баланса. После этого вы можете привести данные к текущим ценам (когда это необходимо). Далее, рассчитайте корреляцию по этим уже обработанным данным. Предложенный метод работает в том случае, если вы используете корреляцию дневных изменений баланса, а не цен. Если вы будете использовать цены, то можете получить искаженную картину, хотя очень часто цены и дневные изменения баланса взаимосвязаны (например, в системе пересечения долгосрочной скользящей средней). Метод удаления тренда следует всегда применять аккуратно. Разумеется, дневное AHPR и стандартное отклонение HPR должны всегда рассчитываться по данным, из которых не удален тренд. Последняя проблема, которая возникает, когда вы удаляете тренд из данных, касается систем, в которых сделки совершаются достаточно редко. Представьте себе две торговые системы, каждая из которых инициирует одну сделку в неделю, [c.216]
Уравнения с квадратными корнями использовались в исследованиях урожайности1, трудоемкости сельскохозяйственного производства. В работе Н. Дрейпера и Г. Смита2 справедливо отмечено, что если нет каких-либо теоретических обоснований в использовании данного вида кривых, то основная цель подобных преобразований состоит в том, чтобы для преобразованных переменных получить более простую модель регрессии, чем для исходных данных. [c.69]
Вторую часть книги, посвященную методам среднесрочного про нозирования, открывает гл. 7, где описывается теория линейной грессии (в случае, когда независимой переменной служит врем этот раздел называется иногда анализом трендов). В гл, 8 рассказ вается, как некоторым преобразованием одной или двух переменны] (зависимой или независимой переменной — время) выравнивание линейной регрессионной модели распространяется на некоторый кла криволинейных зависимостей. В гл, 9 описываются методы подгонк кривых, основанных на модифицированной экспоненте и не сводящи ся к линейной регрессии. Наконец, в последней главе обсуждается пр менение специального метода среднесрочного прогнозирования, из вестного под названием метод кумулятивных сумм — метод корре ции среднесрочных прогнозов. [c.76]
В табл. 7.4 даны нижние и верхние границы 95%-ноге доверительного интервала для этого примера, а на рис. 7.3 эти границы изображены в виде кривых, расположенных по обе стороны от линии регрессии., На том же рисунке показан прогноз затрат в плоть до 1984 г. Возможна, что по этому тренду неделесообразно находить прогноз на более отдаленную перспективу. [c.86]
Кривая Гомпертца и логистическая кривая могут быть получены из другой кривой, известной как модифицированная экспонента, тем же способом, каким были получены из обычной линейной регрессии кривые, рассмотренные в предыдущей главе. В настоящей главе сначала будут рассмотрены вопросы выравнивания и прогнозирования по модифицированной экспоненте, на основе которой с помощью определенных преобразований зависимой переменной будут оцениваться параметры кривой Гампертца и логистической кривой. Все три кривые апробируются на примере с затратами на строительство автомобильных дорог (уже рассмотренного в гл. 7 и 8). Это поможет читателю проверить составленную им программу по выравниванию кривых на контрольном примере. [c.106]
Файл ORRDIM.TXT должен быть переведен в электронную таблицу. Двойная логарифмическая кривая выходного файла даст график, подобный графику рис. 12.2 для аттрактора Хенона. Линейная регрессия применяется к линейному участку этой двойной логарифмической кривой. Ее наклон есть оценка корреляционной размерности. Для аттрактора Хенона размерность вложения известна, поэтому требуется только один ряд в этой размерности. Однако для экспериментальных данных, подобных рыночному временному ряду, размерность вложения нам не известна. Следовательно, мы должны запускать программу неоднократно, увеличивая величины DIMEN до тех пор, пока регрессия не сойдется к единственной величине, как это описано в гл. 13. Эта конвергенция должна произойти до того, как размерность станет слишком большой. В противном случае можно заключить, что данные слишком разрежены для того, чтобы в линейной области подходила двойная логарифмическая кривая. Если налицо такой случай, значит требуется больше данных для оценки размерности, как об этом было сказано в гл. 12 и 13. [c.277]
Таким образом эв-регрессия обладает всеми основными свойствами мнк-регрессии, только наблюдения в соответствующие формулы входят со специально подобранными весами. Введение весов позволяет как бы настраивать регрессию на интересующую исследователя часть выборки (рис. 7.2 в пунктирный овал заключены наблюдения ( , у г), получившие малые веса и практически не участвующие в оценке параметров эв-регрессии куполообразные кривые на прямой эв-регрессии показывают веса, приписанные наблюдениям). Эв-регрессия значительно устойчивее мнк-регрессии и регрессии по Хубе-ру к появлению далеких отклонений от регрессионной поверхности. Однако она, естественно, не является универсальным методом оценки регрессии для всех случаев, когда нарушаются предположения (7.3), лежащие в основе мнк. Четких рекомендаций, как выбирать К в конкретном случае, пока не выработано. Ясно только, что надо давать максимальный вес основной части выборки и наименьший — части, где могут лежать загрязнения . Определенные соображения по выбору величины. К в некоторых модельных случаях приведены в п. 7.2.5. [c.219]
Линия расширения фирмы на ее карте изоквант имеет очевидное геометрическое сходство с потребительской кривой доход—потребление благодаря этому становится ясно, почему авторы, являющиеся последователями Хикса, пришли к использованию термина некачественный фактор , указывая на те факторы, занятость которых сокращается при увеличении объемов производства на фирме и неизменном уровне цен. Сам Хикс никогда не пытался использовать линию расширения в своем графическом анализе совершенно конкурентной фирмы и не использовал термин некачественный фактор . Однако он уделял большое внимание такому странному феномену , как регрессивный фактор eteris paribus уменьшение цен на регрессивный фактор приводит к увеличению предельных затрат и в результате к сокращению выпуска. По наблюдению Хикса, регрессия... является отношением симметричным. Так, если отношение между фактором А и продуктом X характеризуются регрессией, то повышение цены X приведет к расширению объема производства этого продукта, расширению масштабов использования фактора В и сокращению масштабов использования фактора А [3, р. 96 (с. 197-198 русского издания. — Прим. ред.)]. [c.389]
Это вытекает из прим. 4. Если А — регрессивный фактор, то падение цены А приведет к увеличению занятости А и сокращению занятости В при неизменной цене В его занятость сократится только в том случае, если кривая его предельной производительности переместится вниз при увеличении А [3, р. 194]. Отсутствие в отношениях факторов взаимодополняемости является необходимым, но недостаточным условием для того, чтобы их можно было бы рассматривать как некачественные (регрессивные). Вир [1] показывает, что /ху/у < fxyfx необходимо и достаточно в случае с двумя факторами. Этот результат обобщается в случае с га факторами, но не в совсем удобной для интерпретации форме. Так же в случае с п факторами /( > 0 для всех i, j, так что i j исключает низкое качество таким образом, некоторое отсутствие взаимодополняемости необходимо для регрессии. [c.392]
Особую группу Э. м. составляют статистические и стохастические (теоретико-вероятностные) модели. Сюда относятся прежде всего модели, основанные на выравнивании статистич. рядов, напр. а) модели корреляционного исчисления (см. Корреляционные исчисления в статистике), устанавливающие тип зависимости одних статистически характеризуемых явлений от других при помощи т. н. уравнений регрессии, рассчитываемых способом наименьших квадратов, а также тесноту связи между этими явлениями при помощи математически рассчитываемого коэффициента корреляции б) модели статистич. распределения, описывающие к.-л. сложное явление (напр., состояние производительности труда или зарплаты) при помощи ряда рассчитанных параметров распределения (средняя величина, среднее квадратическое отклонение и т, д.) и тео-ретич. кривой распределения вероятностей, построенной на основании этих параметров и являющейся, по существу, математич. моделью реального распределения. К Э. м. стохастического характера, получившим в последнее время большое распространение, относятся модели теории массового обслуживания, к-рыми, напр., описываются процессы многостаночного обслуживания. [c.430]
