Д61 Дисконтирование (учет) векселей-61 [c.456]
П44 Период окупаемости, дисконтированный - 24 1 П74 Поверка средств измерений - 247 [c.470]
Скажем, когда t = 0, стоимость реального основного капитала Va существует за счет неординарного капиталовложения. Во время t=l должно решиться, стоит или не стоит инвестировать сумму I. Если сумма должна инвестироваться, дисконтированная стоимость Vg будет вкладываться во время t = l. Следовательно, стоимость капитала компании состоит из Va и Vg (V = Va + Vg). Теперь независимо от того, когда наступит срок погашения задолженностей — до или после принятия решения об инвестировании, должно начаться погашение долгов Р владельцами облигаций. А и В являются двумя случаями, при которых сроки погашения долгов наступают до и после принятия решения о капиталовложениях. S означает состояние естественного окружения, и компания производит капиталовложения после изучения природного состояния. В случае А , если текущая стоимость прибыли от капиталовложения Vs — I положительна, инвестиция возможна. [c.235]
Подход к оценке через дисконтирование будущих доходов. Понятие дисконтированных будущих доходов. Прогнозирование будущего денежного потока и(или) прибыли. Учет факторного риска. Определение ставки дисконта. Оценка рыночной ожидаемой ставки дохода на собственный капитал. Оценка коэффициента бета и альтернатива ему. Пример анализа дисконтированных будущих доходов. [c.314]
Приведенная стоимость. Чистая приведенная стоимость. Простой и дисконтированный срок окупаемости. Внутренняя норма доходности. Индекс рентабельности. Их характеристики и сравнительный анализ. [c.344]
Цели оценки и виды стоимости недвижимости. Текущая (дисконтированная) стоимость. Рыночная (объективная) стоимость. Капитализированная стоимость. [c.366]
Тема 4. Моделирование стоимости организации при помощи модели дисконтированных денежных потоков. [c.408]
Компьютерная модель дисконтированного денежного потока и стоимость организации. Общая характеристика модели. [c.408]
Доходный подход в оценке недвижимости. Метод валовой ренты Метод капитализации доходов. Метод дисконтированных денежных потоков. [c.421]
Паушальный платеж. Коэффициенты дисконтирования. [c.432]
Концепция временной стоимости денег и математические основы финансового менеджмента. Базовые понятия финансовой математики. Учет фактора времени в оценке затрат и будущих доходов метод аннуитета, метод наращивания и метод дисконтирования. [c.469]
Предположим, что ставка процента равна R. (Пока мы не рассматриваем, какой именно ставкой процента она является. Позднее мы обсудим, как осуществлять выбор между различными видами процентных ставок.) Тогда 1 нынешний доллар может быть инвестирован, чтобы принести 1 + R долларов ровно через год. Следовательно, 1 + R долларов является стоимостью сегодняшнего 1 долл. Какова же нынешняя стоимость, т. е. текущая дисконтированная стоимость (PDV), 1 долл., выплачиваемого через год Ответ прост, раз мы видим, что 1 + R долларов через год стоят (1 -f-R) (l +R) = = 1 долл. сегодня. Таким образом, 1 долл. через год стоит 1 долл./(1 4- R) сегодня. Это то количество денег, которое даст 1 долл. через год, если он приносит прибыль по учетной ставке R. [c.402]
Дисконтированная стоимость 1 долл. [c.403]
Мы можем теперь определить дисконтированную величину доходов по времени. Например, рассмотрим два вида дохода в табл. 14.2. Доход А равен 200 долл. 100 долл., выплачиваемые сейчас, и 100 долл. через год. Доход В равен 220 долл. 20 долл., выплачиваемые сейчас, 100 долл. — через год и еще 100 долл. через два года. Какой из этих двух доходов вы предпочитаете получить Ответ зависит от величины ставки процента. [c.403]
Чтобы рассчитать дисконтированную величину этих доходов, мы вычисляем и складываем дисконтируемую величину каждого года выплат [c.403]
Два вида дисконтированного дохода [c.404]
Вид дисконтированного Дисконтированный доход по годам, долл. [c.404]
В табл. 14.3 приведена дисконтированная величина обоих доходов при ставках 5, 10, 15 и 20%. Как видно из таблицы, предпочтительность дохода зависит от ставки процента. При ставке 10 % или меньше доход В предпочтительнее дохода А. При ставке 15 % или больше доход А предпочтительнее дохода В. Причина заключается в том, что хотя сумма дохода А меньше, но он выплачивается быстрее. [c.404]
Расчет величины дисконтированного дохода при различных ставках [c.404]
Величина дисконтированного дохода при значении процентной ставки, долл. [c.404]
В судебной практике при несчастных случаях пострадавшими или их наследниками (если жертвы погибли) возбуждается дело против нанесшей ущерб стороны (или страховой компании) с целью возмещения ущерба. Кроме компенсации за причиненные боль, страдание и моральные потери, к ущербу относят и будущий доход, который пострадавший или погибший получил бы, не случись несчастья. Чтобы увидеть, как рассчитываются дисконтированные убытки, рассмотрим действительное происшествие 1986 г. (Для сохранения анонимности имена и некоторые данные изменены.) [c.404]
Расчет дисконтированных убытков [c.405]
Дисконтированная стоимость облигации [c.406]
| Рис. 14.1. Дисконтированная сумма дохода от стоимости облигаций. |  |
Уравнения (14.1) и (14.2) показывают, как стоимость двух различных облигаций, зависящую от ставки процента, используют для дисконтирования будущих доходов. Эти уравнения можно развернуть , чтобы показать зависимость стоимости облигации от ставки процента. Это особенно легко сделать в случае с бессрочной облигацией. Предположим, рыночная цена (а значит, и стоимость) бессрочной облигации равна Р. Тогда из уравнения (14.2) следует, что Р = 100 долл./R, a R = 100 долл./Р. Поэтому если цена бессрочной облигации 1000 долл., то ставка процента R=100 долл./ЮОО долл. = 0,10, или 10%. Эту ставку процента называют реальным доходом, или нормой прибыли. Это процент прибыли, получаемой от инвестиций в бессрочные облигации. [c.408]
Критерий чистой дисконтированной [c.411]
Как приходится фирме решать, будут ли те или иные капиталовложения рентабельными Ей следует подсчитать дисконтированную стоимость будущих доходов, ожидаемых от инвестиций, и сравнить ее с размером инвестиций. Это и есть критерий чистой дисконтированной стоимости (NPV) инвестируйте, если ожидаемые доходы больше, чем издержки на инвестиции. [c.411]
Предположим, инвестиции размером С, вероятно, принесут прибыль в следующие десять лет в размере п, Л2,. .., л ю. Тогда мы запишем чистую дисконтированную стоимость как [c.411]
Теперь предположим, что при издержках производства в 42,50 долл. и цене в 52,50 долл. фирма наверняка получит прибыль 80 000 долл. в месяц, или 960 000 долл. в год. Предположим также, что сумма от продажи завода на слом составит 1 млн. долл. Фирма, следовательно, пользуется свободной от риска ставкой процента для дисконтирования будущих прибылей. Записывая доход в млн. долл., составим уравнение для NPV [c.413]
| Рис. 14.3. Графическое изображение дисконтированной стоимости завода | 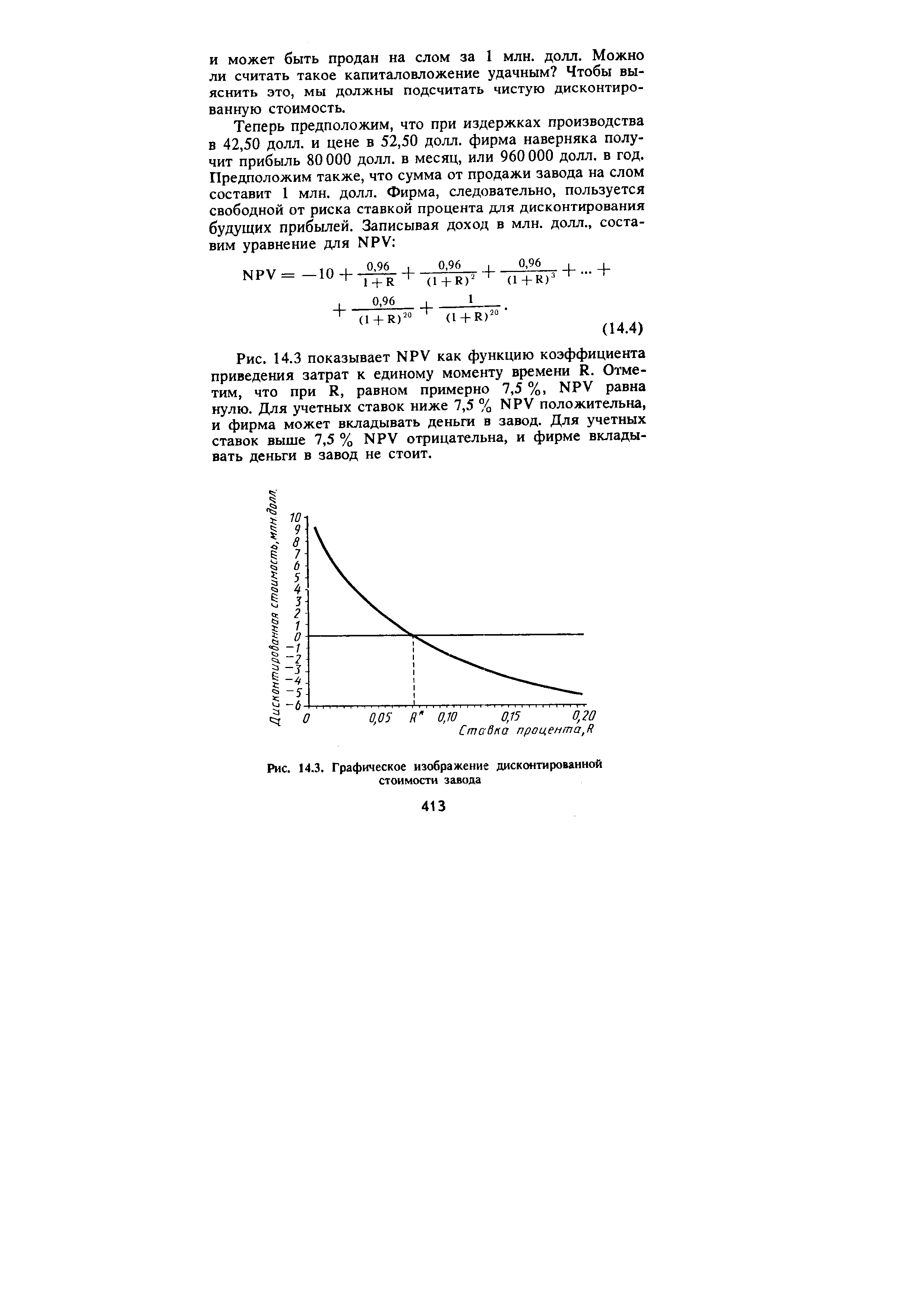 |
Например, предположим, что наш завод электродвигателей будет строиться один год 5 млн. долл. будет потрачено немедленно, а еще 5 млн. долл. — через год. Ожидается, что в первый год работы завод принесет убытки в 1 млн. долл., а во второй год — 0,5 млн. долл. Впоследствии он будет приносить прибыль 0,96 млн. долл. ежегодно на протяжении 20 лет эксплуатации, после чего его продадут на слом за 1 млн. долл. (Все это денежные потоки в реальном выражении.) Тогда чистый дисконтированный доход составляет [c.415]
Когда фирма вкладывает капитал, она тратит деньги сегодня, чтобы получить доход в будущем. Чтобы решить, выгодны ли капиталовложения, фирма должна определить дисконтированную сумму будущих доходов. Она осуществляет это, дисконтируя будущие доходы. [c.416]
Дисконтированная стоимость (PDV) 1 долл., выплаченного через год, равна 1 долл./(1-f R), где R — ставка процента. PDV 1 долл., выплаченного через п лет, составляет 1 долл./(1 + R)". [c.416]
Рассчитывается на основе дисконтирования финансовых потоков и позволяет учесть зависимость между капиталом и временем. Вопрос о соизмерении денежных средств, затрачиваемых и получаемых в различные месяцы и годы, решается с помощью использования понятия "interest", что в переводе с английского означает "интерес" или "процент". Эту величину называют нормой дисконтирования, нормой прибыли или процентной ставкой. [c.241]
В табл. 14.1 приведена для различных ставок процента текущая дисконтированная стоимость 1 долл., выплачива- [c.402]
За 1986 г. его зарплата составила бы 85000 долл., а возраст выхода на пенсию летного состава равен 60 годам. Чтобы подсчитать дисконтированные убытки г-на Дженнингса, мы должны учесть три аспекта. Во-первых, его сумма дохода, вероятно, возросла бы со временем. Во-вторых, мы не можем быть уверены, что он дожил бы до пенсии, даже если бы не произошел данный несчастный случай. Он мог бы скончаться и по какой-нибудь другой причине. Следовательно, сумма его дисконтируемых убытков вплоть до выхода на пенсию в 1993 г. составляет [c.405]
Смотреть страницы где упоминается термин Дисконтирование
: [c.61] [c.140] [c.241] [c.462] [c.236] [c.402] [c.405] [c.413] [c.415]Финансовый анализ - методы и процедуры (2001) -- [ c.464 , c.465 ]
Количественные методы анализа хозяйственной деятельности (1999) -- [ c.141 ]
Принципы корпоративных финансов (1999) -- [ c.100 , c.101 , c.102 , c.105 , c.106 , c.246 , c.512 , c.513 , c.514 , c.515 ]
1000 терминов рыночной экономики (1993) -- [ c.75 ]
Финансовый анализ и планирование хозяйствующего субъекта (2002) -- [ c.158 ]
Экономико-математический словарь Изд.5 (2003) -- [ c.87 ]
Организация и финансирование инвестиций (2001) -- [ c.74 , c.167 , c.171 ]
Финансово кредитный словарь Том 1 (1961) -- [ c.386 ]
50 лекций по микроэкономике Том 2 (2000) -- [ c.2 , c.150 , c.191 , c.338 , c.636 , c.647 , c.733 ]
Популярный экономико-математический словарь (1973) -- [ c.95 ]
Денежно-кредитный энциклопедический словарь (2006) -- [ c.86 ]
Курс экономической теории Изд5 (2006) -- [ c.12 ]
Большая экономическая энциклопедия (2007) -- [ c.191 , c.205 , c.208 , c.292 , c.514 ]
